
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретический материал. Многогранник – это тело, граница которого состоит из кусков плоскостей (многоугольников)
Многогранник – это тело, граница которого состоит из кусков плоскостей (многоугольников). Эти многоугольники называются гранями, их стороны – рёбрами, их вершины – вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник – выпуклый, если все его диагонали расположены внутри него.
Призма – это многогранник (рис.79), две грани которой ABCDE и abcde (основания призмы) – равные многоугольники с соответственно параллельными сторонами, а остальные грани (A ab B, B bc C и т.д.) - параллелограммы, плоскости которых параллельны прямой (A a, или B b, или C c и т.д.). Параллелограммы A ab B, B bc C и т.д. называются боковыми гранями; рёбра A a, B b, C c и т.д. называются боковыми рёбрами. Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае – это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной. На рис.79 показана наклонная призма.
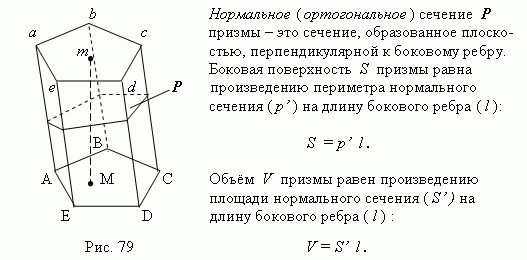
Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда
четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам. Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным. Диагональ прямоугольного параллелепипеда d и его рёбра a, b, c связаны соотношением: d 2 = a 2 + b 2 + c 2. Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все рёбра куба равны.
Пирамида – это многогранник, у которого одна грань (основание пирамиды) – это произвольный многоугольник (ABCDE, рис.80), а остальные грани (боковые грани) – треугольники с общей вершиной S, называемой вершиной пирамиды. Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром (четырёхгранником), четырёхугольная – пятигранником и т.д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.
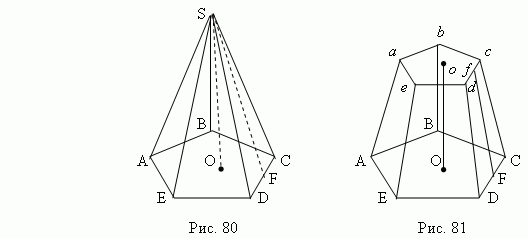
Если провести сечение abcde, параллельное основанию ABCDE (рис.81) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние O o между ними – высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная. Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота F f боковой грани (рис.81) называется апофемой правильной усечённой пирамиды.
Решение примеров и задач (алгоритм выполнения задания):
Задача 1.

Чему равна площадь боковой поверхности правильной четырёхугольной пирамиды со стороной в основании 4,5см и апофемой 5см?
А. 90см2 Б. 45см2 В. 101,25см2
Задача 2.

Вычислите объём правильной треугольной пирамиды со стороной в основании 6 дм и высотой пирамиды 8 дм.
А. 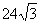 дм3 Б.
дм3 Б. 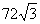 дм3 В.
дм3 В. 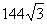 дм3
дм3
Задача 3.
Какой объём имеет деревянная шпала длиной 2,7 м, толщиной 0,18 м и шириной 0,25 м.
А. 3,13м3 Б. 0,1215м3 В. 0,531м3
Правильные ответы
· Задача 1: Б. 45см2;
· Задача 2: А 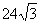 дм3;
дм3;
· Задача 3: Б. 0,1215м3.
Решите примеры:
Задачи
| 3 балла | Вычислить площадь боковой поверхности и объём призмы или пирамиды, сделав необходимые измерения. | |
| 4 балла | 
| Сколько штук досок размером 100 мм на 2500 мм потребуется на обшивку крыши и потолка сарая, длина крыши 4 м, ширина 3 м, а высота 2 м. Крыша имеет форму прямой треугольной призмы, в основании которой равнобедренный треугольник. На отходы уходит 5% от всего материала. |
| 5 баллов | 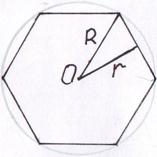
| Какова масса заготовки стального шестигранного прутка длиной 1м, имеющего 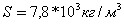 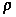 =7,8 =7,8  103 кг/м3 и o =14 103 кг/м3 и o =14
|
После решения задач необходимо ответить на вопросы:
– Какие данные вам были необходимы для вычислений?
– По какой формуле вычисляли  призмы?
призмы?
– По какой формуле вычисляли  пирамиды?
пирамиды?
– По какой формуле вычисляли V фигуры?
– По какой формуле вычисляли S основания?
Вопросы для самоконтроля:
1.Как называется фигура, состоящая из двух равных многоугольников, лежащих в параллельных плоскостях, и n параллелограммов?
1. Как называются стороны граней многогранника?
2. Как называется отрезок, соединяющий две вершины, не принадлежащие одной грани?
3. У какой призмы боковые ребра перпендикулярны к основаниям?
4. Что выражается этой формулой 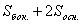 ?
?
5. Как называется высота боковой грани правильной пирамиды?
6. Что выражается этой формулой 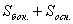 ?
?
7. Какой многоугольник лежит в основании правильной призмы?
8. Что вычисляется по этой формуле 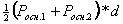 ?
?
9. По какой формуле вычисляется объем пирамиды?
10. Какая фигура является боковой гранью призмы?
11. Как называется фигура, состоящая из многоугольников и n треугольников?
12. Как называются концы ребер?
13. Какой многогранник лежит в основании правильной пирамиды?
14. Что у прямой призмы может являться высотой?
15. Что вычисляется по этой формуле 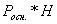 ?
?
16. Как называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
17. По какой формуле вычисляется площадь боковой поверхности правильной пирамиды?
18. Какая фигура является боковой гранью усеченной пирамиды, усеченной правильной пирамиды?
19. По какой формуле вычисляется объем призмы?
20. Какая фигура является боковой гранью пирамиды, правильной пирамиды?
21. Приведите примеры предметов из окружающего мира, которые имеют вид призм и пирамид
. Рекомендуемая литература:
Основные источники:
1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.
2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
Дополнительные источники:
1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.
3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.
4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.
5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.
6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.
7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.
8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.
9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.
10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.
11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.
12. Пехлецкий И.Д. Математика: учебник. – М., 2003.
13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.
Интернет ресурсы:
1.Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307
2.Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович
e-ypok.ru/content/
3. Математика для колледжей» Математический Портал – библиотека math-portal.ru
Не нашли, что искали? Воспользуйтесь поиском: