Предел последовательности.

Пусть есть последовательность { c_n } = {1/ n }. Эту последовательность называют гармонической, поскольку каждый ее член, начиная со второго, есть среднее гармоническое между предыдущим и последующим членами. Среднее геометрическое чисел a и b есть число 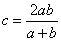, или . С ростом n все члены геометрической прогрессии убывают и их значение приближается к нулю. В этом случае принято говорить, что при n, стремящемся к бесконечности, данная последовательность сходится и нуль есть ее предел. Записывается это так:

.

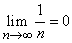Строгое определение предела формулируется следующим образом:

Если существует такое число A, что для любого (сколь угодно малого) положительного числа e найдется такое натуральное N (вообще говоря, зависящее от e), что для всех n N будет выполнено неравенство | a_n – A | < e, то говорят, что последовательность { a_n } сходится и A – ее предел.

Обозначается это так: .

В противном случае последовательность называется расходящейся.

Опираясь на это определение, можно, например, доказать наличие предела A=0 у гармонической последовательности { c_n } = {1/ n }. Пусть e – сколь угодно малое положительное число. Рассматривается разность

.

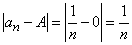Существует ли такое N, что для всех n N выполняется неравенство 1 /N< e? Если взять в качестве N любое натуральное число, превышающее 1 / e, то для всех n і N выполняется неравенство 1 /n < 1 /N < e, что и требовалось доказать.

Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.

Теорема 1. Если последовательность имеет предел, то она ограничена.

Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.

Теорема 3. Если последовательность { a_n } имеет предел A, то последовательности { ca_n }, { a_n + с} и {| a_n |} имеют пределы cA, A + c, | A | соответственно (здесь c – произвольное число).

Теорема 4. Если последовательности { a_n } и { b_n } имеют пределы, равные A и B соответственно, то последовательность { pa_n + qb_n } имеет предел pA + qB.

Теорема 5. Если последовательности { a_n } и { b_n }имеют пределы, равные A и B соответственно, то последовательность { a_nb_n } имеет предел AB.

Теорема 6. Если последовательности { a_n } и { b_n } имеют пределы, равные A и B соответственно, и, кроме того, b _n 0 и B 0, то последовательность { a_n / b_n } имеет предел A/B.

Решение примеров и задач (алгоритм выполнения задания):

Найти пределы:

1. ; 5. ;

2. ; 6. ;

3. ; 7. ;

4. ; 8. .

Решение:

Пример 1. .

Решение: .

Пример 2. .

Решение: При имеем неопределённость вида «».

Разделим числитель и знаменатель на , тогда

, так как при отношения стремятся к 0.

Пример 3. .

Решение: При имеем неопределённость вида «».

Умножим числитель и знаменатель на выражение , которое является сопряжённым для выражения, стоящего в знаменателе:

Пример 4. .

Решение: При числитель и знаменатель стремятся к нулю. Разложим их на множители:

.

Пример 5. .

Решение: При имеем неопределённость вида «0 · ∞».

Преобразуем данную функцию для того, чтобы использовать первый замечательный предел: .

.

Пример 6. .

Решение: При имеем неопределённость вида «».

Чтобы раскрыть эту неопределённость, представим основание степени в виде , а в показателе степени выделим множитель , чтобы использовать второй замечательный предел: .

Для этого обозначим , тогда и при имеем .

.

Пример 7. .

Решение: При имеем неопределённость вида «».

В числителе выражения находится сумма членов арифметической прогрессии , которая вычисляется по формуле .

В нашем случае и, следовательно: .

Разделив числитель и знаменатель на , получим:

Пример 8. .

Решение: При получаем неопределённость вида «». Умножим и поделим выражение в скобках на сопряжённое выражение :

Решите примеры:

Пример 1. Первый член арифметической прогрессии () равен 1, а знаменатель . Найти: .

Пример 2. Первый член арифметической прогрессии () равен 3, а знаменатель . Найти: .

Пример 3. Первый член геометрической прогрессии () равен 5, а знаменатель 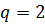. Найти: .

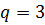Пример 4. Первый член геометрической прогрессии () равен 4, а знаменатель . Найти: .

Найти пределы:

1. ; 5. ;

2. ; 6. ;

3. ; 7. ;

4. ; 8. .

Вопросы для самоконтроля:

1. Какие способы существует задания числовой последовательности?

2. Что такая числовая последовательность?

3. Что такая арифметическая прогрессия?

4. Что такая разность арифметической прогрессии?

5. Что такая геометрическая прогрессия?

Рекомендуемая литература:

Основные источники:

1. Башмаков М.И., математика: учебник для нач. и сред. Проф. образования, -М.: Образовательно-издательский центр «Академия», 2010.- 256 с.

2. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

4. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

5. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

Дополнительные источники:

1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000.

3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005.

4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005.

5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005.

6. Башмаков М.И. Математика: 10 кл. Сборник задач: учеб. пособие. – М., 2004.

7. Башмаков М.И. Математика: учебник для 10 кл. – М., 2004.

8. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000.

9. Колягин Ю.М. и др. Математика (Книга 1). – М., 2003.

10. Колягин Ю.М. и др. Математика (Книга 2). – М., 2003.

11. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004.

12. Пехлецкий И.Д. Математика: учебник. – М., 2003.

13. Смирнова И.М. Геометрия. 10 (11) кл. – М., 2000.

Интернет ресурсы:

1. Колмогоров А.Н. (ред.) — Алгебра и начала анализа: Электронная книга. Lib.mexmat.ru/books/3307

2. Алгебра и начала анализа. 10-11 класс. Учебник. Мордкович

e-ypok.ru/content/

3. Математика для колледжей» Математический Портал – библиотека math-portal.ru

Не нашли, что искали? Воспользуйтесь поиском: