
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Неравенство Чебышева
Если случайная величина  имеет конечное математическое ожидание и дисперсию, то для любого положительного числа
имеет конечное математическое ожидание и дисперсию, то для любого положительного числа  справедливо неравенство
справедливо неравенство
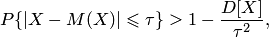
| (9.1) |
то есть вероятность того, что отклонение случайной величины  от своего математического ожидания по абсолютной величине не превосходит
от своего математического ожидания по абсолютной величине не превосходит  и больше разности между единицей и отношением дисперсии этой случайной величины к квадрату
и больше разности между единицей и отношением дисперсии этой случайной величины к квадрату  .
.
Запишем вероятность события 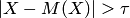 , то есть события, противоположного событию
, то есть события, противоположного событию  . Очевидно, что
. Очевидно, что

| (9.2) |
Неравенство Чебышева справедливо для любого закона распределения случайной величины  и применимо как к положительным, так и к отрицательным случайным величинам. Неравенство (9.2) ограничивает сверху вероятность того, что случайная величина отклонится от своего математического ожидания на величину больше
и применимо как к положительным, так и к отрицательным случайным величинам. Неравенство (9.2) ограничивает сверху вероятность того, что случайная величина отклонится от своего математического ожидания на величину больше  . Из этого неравенства следует, что при уменьшении дисперсии верхняя граница вероятности также уменьшается, и значения случайной величины с небольшой дисперсией сосредотачиваются около её математического ожидания.
. Из этого неравенства следует, что при уменьшении дисперсии верхняя граница вероятности также уменьшается, и значения случайной величины с небольшой дисперсией сосредотачиваются около её математического ожидания.
Теорема Чебышева
При достаточно большом числе независимых испытаний  с вероятностью, близкой к единицы, можно утверждать, что разность между средним арифметическим наблюдавшихся значений случайной величины
с вероятностью, близкой к единицы, можно утверждать, что разность между средним арифметическим наблюдавшихся значений случайной величины  и математическим ожиданием этой величины
и математическим ожиданием этой величины  по абсолютной величине окажется меньше сколь угодно малого числа
по абсолютной величине окажется меньше сколь угодно малого числа  при условии, что случайная величина
при условии, что случайная величина  имеет конечную дисперсию, то есть
имеет конечную дисперсию, то есть

где  — положительное число, близкое к единице.
— положительное число, близкое к единице.
Переходя в фигурных скобках к противоположному событию, получаем

Теорема Чебышева позволяет с достаточной точностью по средней арифметической судить о математическом ожидании или, наоборот, по математическому ожиданию предсказывать ожидаемую величину средней. Так, на основании этой теоремы можно утверждать, что если проведено достаточно большое количество измерений определённого параметра прибором, свободным от систематической погрешности, то средняя арифметическая результатов этих измерений сколь угодно мало отличается от истинного значения измеряемого параметра.
Теорема Бернулли
Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.
При достаточно большом числе независимых испытаний  с вероятностью, близкой к единице, можно утверждать, что разность между относительной частой появления события
с вероятностью, близкой к единице, можно утверждать, что разность между относительной частой появления события  в этих испытаниях е го вероятностью в отдельном испытании по абсолютной величине окажется меньше сколь угодно малого числа
в этих испытаниях е го вероятностью в отдельном испытании по абсолютной величине окажется меньше сколь угодно малого числа  , если вероятность наступления этого события в каждом испытании постоянна и равна
, если вероятность наступления этого события в каждом испытании постоянна и равна  .
.
Утверждение теоремы Бернулли можно записать в виде неравенства

| (9.3) |
где  — любые сколь угодно малые положительные числа.
— любые сколь угодно малые положительные числа.
Используя свойства математического ожидания и дисперсии, а также неравенство Чебышева, формулу (9.3) можно записать в виде
| (9.4) |
При решение практических задач иногда бывает необходимо оценить вероятность наибольшего отклонения частоты появлений события от её ожидаемого значения. В этом случае случайной величиной является число появления события  в
в  независимых испытаниях. Имеем
независимых испытаниях. Имеем
Используя неравенство Чебышева, получаем

Теорема Ляпунова
Рассмотренные теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определённым предельным значениям независимо от их закона распределения. В теории вероятностей существует другая группа теорем, касающихся предельных законов распределения суммы случайных величин. Общее название этой группы теорем — центральная предельная теорема. Различными её формы различаются условиями, накладываемыми на сумму составляющих случайных величин.
Закон распределения суммы независимых случайных величин  приближается к нормальному закону распределения при неограниченном увеличении
приближается к нормальному закону распределения при неограниченном увеличении  , если выполняются следующие условия:
, если выполняются следующие условия:
1) все величины имеют конечные математические ожидания и дисперсии:
 где
где  .
.
2) ни одна из величин по значению резко не отличается от остальных:
При решении многих практических задач используют следующую формулировку теоремы Ляпунова для средней арифметической наблюдавшихся значений случайной величины  , которая также является случайной величиной (при этом соблюдаются перечисленные два условия):
, которая также является случайной величиной (при этом соблюдаются перечисленные два условия):
если случайная величина  имеет конечные математическое ожидания
имеет конечные математическое ожидания  и дисперсию
и дисперсию  , то распределение средней арифметической
, то распределение средней арифметической  , вычисленной по наблюдавшимся значениям случайной величины в
, вычисленной по наблюдавшимся значениям случайной величины в  независимых испытаниях, при
независимых испытаниях, при  приближается к нормальному закону с математическим ожиданием
приближается к нормальному закону с математическим ожиданием  и дисперсией
и дисперсией  , то есть
, то есть
Поэтому вероятность того, что  заключена в интервале заключена в интервале  , можно вычислить по формуле(9.5) , можно вычислить по формуле(9.5)
|
Используя функцию Лапласа формулу (9.5) можно записать в удобном для расчётов виде:
 где
где
Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный.
40. Локальная теорема Муавра-Лапласа.
Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина  ограничена равномерно по m и n
ограничена равномерно по m и n  , то
, то

где  , c > 0, c - постоянная.
, c > 0, c - постоянная.
Приближённую формулу

рекомендуется применять при n > 100 и npq > 20.
Доказательство
Для доказательства Теоремы будем использовать формулу Стирлинга из математического анализа:
 (1)
(1)
где 0 < θ s < 1 / 12 s. При больших s величина θ очень мала, и приближённая формула Стирлинга, записанная в простом виде,
 (2)
(2)
даёт малую относительную ошибку, быстро стремящуюся к нулю, когда  .
.
Нас будут интересовать значения m, не очень отличающиеся от наивероятнейшего. Тогда при фиксированном p условие  будет так же означать, что
будет так же означать, что
 ,
,  (3)
(3)
Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем
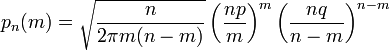 (4)
(4)
Также понадобится использование отклонения относительной частоты от наивероятнейшего значения
 (5)
(5)
Переписываем полученное ранее биномиальное распределение с факториалами, заменёнными по приближённой формуле Стирлинга:
 (6)
(6)
Предположим, что
xm < pq (7)
Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора:
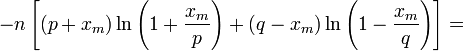
 (8)
(8)
Располагаем члены этого разложения по степеням xm:
 (9)
(9)
Предположим, что при 
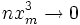 (10)
(10)
Это условие, как уже было указанно выше, означает, что рассматриваются значения m, не очень далёкие от наивероятнейшего. Очевидно, что (10) обеспечивает выполнение (7) и (3).
Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен
 (11)
(11)
Отбрасывая малые слагаемые в скобках первого множителя (6), получаем:
 (12)
(12)
Обозначив
 (13)
(13)
Переписываем (12) в виде:
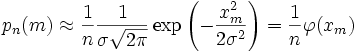 (14)
(14)
Где 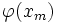 — нормальная функция.
— нормальная функция.
Поскольку в интервале [ m, m + 1) имеется только одно целое число m, то можно сказать, что pn (m) есть вероятность попадания m в интервал [ m, m + 1). Из (5) следует, что изменению m на 1 соответствует изменение xm на
 (15)
(15)
Поэтому вероятность попадания m в интервал [ m, m + 1) равна вероятности попадания xm в промежуток [ xm, xm + Δ x)
 (16)
(16)
Когда  ,
,  и равенство (16) показывает, что нормальная функция
и равенство (16) показывает, что нормальная функция 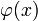 является плотностью случайной переменной xm
является плотностью случайной переменной xm
Таким образом, если 
 то для отклонения относительной частоты от наивероятнейшего значения справедлива ассимптотическая формула (16), в которой
то для отклонения относительной частоты от наивероятнейшего значения справедлива ассимптотическая формула (16), в которой 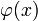 — нормальная функция с xm = 0 и
— нормальная функция с xm = 0 и  .
.
Таким образом теорема доказана.
41. Интегральная теорема Муавра-Лапласа.
Если вероятность  события
события  в каждом испытании постоянна и отлична как от нуля, так и от единицы, то вероятность
в каждом испытании постоянна и отлична как от нуля, так и от единицы, то вероятность  того, что событие
того, что событие  появится в
появится в  испытаниях от
испытаниях от  до
до  раз, приближенно равна определенному интегралу:
раз, приближенно равна определенному интегралу:
 ,
,
где  ,
,  .
.
Доказательство. На основании теоремы сложения вероятности для несовместных событий:
 .
.
Отсюда, используя локальную теорему Лапласа:
 ,
,
где  (
( );
);  .
.
Поскольку  ,
,
следовательно  .
.
Причем, эта сумма является интегральной для функции  на отрезке
на отрезке 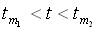 , так как при
, так как при  , т.е. при
, т.е. при  , ее предел равен соответствующему определенному интегралу:
, ее предел равен соответствующему определенному интегралу:
 ,
,
где  , а
, а  ,
,
что и требовалось доказать.
Введем стандартный интеграл Лапласа (функцию Лапласа):
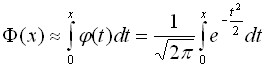 ,
,
который, очевидно, является первообразной функции Гаусса:
 .
.
Тогда на основании формулы Ньютона – Лейбница можно записать
 .
.
Значения функций  и
и  обычно находятся из таблиц, причем таблицы обычно даны лишь для неотрицательных значений
обычно находятся из таблиц, причем таблицы обычно даны лишь для неотрицательных значений  , поскольку
, поскольку  – четная функция, а
– четная функция, а  – нечетная. Из таблиц видно, что при
– нечетная. Из таблиц видно, что при  значения
значения  практически не отличаются от 0.5, поэтому далее табуляция, как правило, не ведется.
практически не отличаются от 0.5, поэтому далее табуляция, как правило, не ведется.
42. Основные понятия математической статистики.
Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей.
Математическая статистика тесно связана с теорией вероятностей. Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений.
Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.
Зачастую проводить сплошное обследование, когда изучаются все объекты, трудно или дорого, а иногда и невозможно. В этих случаях наилучшим способом обследования является выборочное наблюдение: выбирают из генеральной совокупности часть ее объектов («выборку») и подвергают ее изучению.
Выборочной совокупностью (выборкой) называют совокупность объектов, отобранных случайным образом из генеральной совокупности. Более строго:
выборка – это последовательность X 1, X 2, … Xn независимых одинаково
распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.
Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом; обозначается соответственно через N и n.
Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами x 1, х 2 … хn.
Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным.
Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором – не возвращается. На практике чаще используется бесповторная выборка
43. Оценка числовых характеристик случайных величин.
44. Оценка математического ожидания и дисперсии, их свойства.
Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Рассмотрим некоторые из числовых характеристик и их основные свойства.
Не нашли, что искали? Воспользуйтесь поиском: