
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Нормальное распределение.
Случайная непрерывная величина X имеет нормальное (гауссово) распределение, если ее плотность распределения вероятности имеет вид
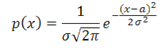
где  — среднее квадратическое отклонение; а — математическое ожидание.
— среднее квадратическое отклонение; а — математическое ожидание.
Если а=0 и σ=1, то нормальное (гауссовое) распределение называется стандартным нормальным (гауссовым) распределением (таблица плотности вероятности нормальной случайной величины), плотность которого равна

а функция распределения (функция Лапласа) (таблица функции Лапласа)

Вероятность попадания в заданный интервал (α;β) нормально распределенной случайной величины с параметрами а, σ вычисляется по формуле:

с использованием интеграла вероятности
| P(α<x<β)=F(α)-F(β)=Ф( | β-a | ) |
| σ |
| -Ф( | α-a | ) |
| σ |
Из этих соотношений легко получить вероятность отклонения распределения случайной величины X от своего математического ожидания а:
| P(|X-a|<δ)=2Ф( | δ | ) |
| σ |
,где δ — величина отклонения.
Полагая в этой формуле δ=3σ, получаем
P(|X-a|<δ)=2Ф(3)=2*0.49865=0.9973
Этот результат носит название «правило трех сигм». Таким образом, в 99,7% случаях все значения нормального распределения случайной величины сосредоточены в интервале (-3σ+a; 3σ+a). Распределение, заданное на бесконечном интервале, может быть рассмотрено на конечном интервале, и погрешность при такой замене равно,примерно, 0,3%.
29. Показательное распределение. Функция надёжности.
Показательным (экспоненциальным) называют распределение верояйюстей, которое описывается дифференциальной функцией

где ?— положительная постоянная величина.
Мы видим, что показательное распределение определяется одним параметром?. Эта особенность показательного распределения указывает на его преимущество, по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения); разумеется, проще оценить один параметр, чем два, или три и т. д.
Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
Найдем интегральную функцию показательного распределения.

Мы определили показательное распределение при помощи дифференциальной функции; ясно, что его можно определить, пользуясь интегральной функцией.
Графики дифференциальной и интегральной функций изображены на рис. 12.
Функцией надежности R(f) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t: R(t)=P(T>t)
Часто длительность времени безотказной работы элемента имеет показательное распределение, интегральная функция которого
F(t)=1-e-?t
Следовательно, в силу соотношения R(t)=P(T>t)=1-F(t) предыдущего параграфа, функция надежности, в случае показательного
распределения времени безотказной работы элемента, имеет вид 
П
 оказательным законом надежности называют функцию надежности, определяемую равенством
оказательным законом надежности называют функцию надежности, определяемую равенством
(*)
где?, — интенсивность отказов.
Как следует из определения функции надежности (§ 4), эта формула позволяет найти вероятность безотказной работы элемента на интервале времени, длительностью t, если время безотказной работы имеет показательное распределение.
Не нашли, что искали? Воспользуйтесь поиском: