ДОТЕПНІ ЗАДАЧІ З ЛОГІКИ

Висновки

Щоб відновити в силогізм ентимему з пропущеним засновком, необхідно:

1. Встановити тип суджень, які входять до складу ентимеми.

2. Знайти висновок ентимеми.

3. Знайти терміни силогізму.

4. Встановити, яким є наявний засновок і який засновок пропущений.

5. Визначити тип судження пропущеного засновку.

6. Визначити фігуру і модус силогізму, з якого утворена ентимема.

7. Перевірити відновлений силогізм за всіма правилами простого категоричного силогізму.

5.5. Розв’язання задач на категоричний
силогізм за допомогою діаграм Венна

Серед різних видів дедуктивних умовиводів важливе місце займає категоричний силогізм. Однак загальні правила силогізму і спеціальні правила його фігур, розроблені традиційною (арістотелівською) логікою, не дають змоги перевірити надійним способом логічну правильність силогізмів у тих випадках, коли якесь поняття (клас) виявиться пустим. Ми знаємо, що арістотелівська силогістика не оперувала поняттям «пусте». Діаграми Ейлера були створені відповідно до потреб арістотелівської силогістики і пристосовані до неї. Тому з огляду на вимоги сучасної формальної логіки діаграми Ейлера не можуть вважатися надійним в усіх випадках способом відбору правильних модусів категоричного силогізму, оскільки з діаграм Ейлера не видно, чи є середній термін (М) пустим чи непустим.

Ефективним методом перевірки логічної правильності категоричних силогізмів є діаграми Венна. Як відомо, діаграми Венна являють собою графічне зображення обсягів понять (класів, множин) за допомогою кіл або інших замкнутих контурів, що перетинаються, введено наприкінці ХІХ ст. англійським логіком Джоном Венном (1834—1923).

Щоб діаграми Венна можна було застосовувати для аналізу логічної правильності висновків у категоричних силогізмах, необхідно записати категоричні судження (а, е, і, о) мовою класів. З цією метою всі чотири види категоричних суджень подаємо спочатку у такому записі:

(а) Всі А є В, або аАВ

(е) Жодне А не є В, або еАВ

(і) Деякі А є В, або іАВ

(о) Деякі А не є В, або оАВ

Терміни (А, В) категоричних суджень (а, е, і, о) розглядатимемо як класи, які є частинами деякого універсального класу.

Ми знаємо, що відношення двох класів К Ì М еквівалентне КМ¹=Æ. Виходячи з цього відношення, маємо право записати категоричні судження за допомогою пустого класу:

аАВ º АВ¹ = Æ (АВ¹ пусте);

еАВ º АВ = Æ (АВ пусте);

іАВ º АВ ¹ Æ (АВ не пусте);

оАВ º АВ¹ ¹ Æ (АВ¹ не пусте).

Такий запис категоричних суджень дає змогу зображувати їх графічно за допомогою діаграм Венна для двох класів (множин).

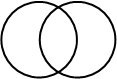
Діаграма Венна для двох класів (А, В) має такий вигляд*:

Рис. 1

Як бачимо, у діаграмі Венна два кола, що перетинаються, розбивають універсальний клас на чотири області:

1) АВ¹ — клас предметів (зU), що належать до класу А і не належать до класу В (АВ¹ = А – В).

2) АВ — клас предметів (зU), що належить до класу А і до класу В.

3) А¹В— клас предметів (зU), що належить до класу В і не належить до класу А (А¹В = В – А).

4) А¹В¹ — клас предметів (зU), що не належить ні до класу А, ні до класу В, тобто належить до А¹ і В¹.

Домовимося зазначати штрихуванням ті області діаграми Венна, які відповідають пустим класам, і точкою (представленою в середині області) ті області діаграми, які відповідають непустим класам. Тоді схеми категоричних суджень графічно зобразяться так, як це показано на рис. 2.

Рис. 2

Тепер все сказане вище про категоричні судження легко звести у таку таблицю:

Форма судження	Надається смисл (обсяжна інтерпретація)	Запис мовою «пусте — непусте»	Графічне зображення за допомогою діаграм Венна
Будь-яке А є В. (аАВ)	Не існує (немає) предметів, які належать до класу А, але не належать до класу В	АВ1 = Æ
Жодне А не є В. (еАВ)	Не існує предметів, що належать до класу А і до класу В	АВ = Æ
Деякі А є В. (іАВ)	Існують предмети, які належать до класу А і до класу В	АВ ¹ Æ
Деякі А не є В. (оАВ)	Існують предмети, які належать до класу А, але не належать до класу В	АВ1 ¹ Æ

З геометричних моделей категоричних суджень (діаграм Венна) видно, що еАВ º еВА та іАВ º іВА. Ці еквівалентності можна легко побачити також із запису даних суджень, оскільки перетин класів комутативний: АВ º ВА.

Оскільки до складу категоричного силогізму входять три терміни (класи), то діаграма Венна для цього силогізму складається з трьох кіл, що взаємно перетинаються (див. рис. 3.).

Рис. 3

Ці кола розбивають універсальний клас на 17 областей, 8 з яких утворено трьома колами (рис. 3), а останні 9 — кожною парою кіл окремо (рис. 4—12; на рис. 4—12 відповідні області заштриховані).

Під час перевірки категоричних силогізмів на логічну правильність за допомогою діаграм Венна будемо керуватися такими положеннями: (1) на діаграмі менший термін силогізму позначатимемо латинською буквою А, більший — буквою В, середній — буквою М; (2) засновки формалізуватимуться за допомогою пустого класу і зображатимуться на діаграмі так, як це показано на рис. 2; (3) штриховка області показує, що вона пуста; (4) точка в області показує, що область непуста; (5) чисті області (без штриховок і точок) можуть бути як пустими, так і непустими; (6) якщо неясно, де знаходиться непустий клас, то точка сполучається прямою лінією з іншими точками, щоб показати багатозначність непустого класу (отже, часткові засновки на діаграмі для трьох класів повинні зображатися за допомогою двох точок, сполучених між собою лінією); (7) з діаграми ми повинні побачити (якщо це можливо) відношення між класами, які відповідають крайнім термінам силогізму (А, В). Аналіз діаграми зводиться до з’ясування того, яка з трьох областей АВ¹, АВ і А¹В (ВА¹) пуста або непуста.

Рис. 4 Рис. 5 Рис.6

Рис. 7. Рис. 8 Рис. 9

Рис. 10 Рис. 11 Рис. 12

Рис. 13

Приклад 1. Перевірити, чи буде правильним силогізм, модус якого:

аАМ АМ¹ = Æ

еМВМВ = Æ

еАВ АВ = Æ

Перш за все записуємо судження силогізму за допомогою пустого класу (цей запис вміщено поруч з модусом силогізму). Потім будуємо діаграму Венна для трьох класів А, В і М і заштриховуємо у ній область АМ¹ (вона охоплює АВ¹М¹ і АВМ¹), пустота якої випливає з першого засновку (АМ¹ = Æ), а також область МВ (вона охоплює АВМ і А¹ВМ), пустота якої випливає з другого засновку (МВ = Æ). Тепер, розглядаючи класи А і В, помічаємо, що область АВ (вона охоплює АВМ¹ і АВМ) заштрихована, а це означає, що вона пуста. Отже, пустота області АВ на діаграмі (АВ = Æ) збігається з висновком модусу (АВ = Æ). Правильність модусу доведена.

Рис. 14

Приклад 2. Перевірити правильність силогізму, який має модус:

іМА МА ¹ Æ

аМВМВ¹ = Æ

іВА ВА ¹ Æ

Перший засновок показує, що область МА (складена з АМВ¹ і АМВ) не є пустою. Щоб зобразити це, проведемо лінію (пряму) через область МА, з’єднуючи точку АМВ¹ з точкою області АМВ. Ця операція викликана тим, що нам невідомо, чи розташована точка по той або по інший бік від границі класу В. Тому ми малюємо дві точки і з’єдну­ємо їх рискою, яка перетинає границю зазначених двох областей, щоб виразити цю невизначеність. Потім заштриховуємо область МВ¹ (вона охоплює АМВ¹ і А¹МВ¹), бо про її пустоту говорить другий засновок. Розглядаючи класи А і В, помічаємо, що область АВ (або ВА) є непустою, оскільки область АМВ є непустою (внаслідок того, що область АМВ є частиною області АВ, а область АМВ є непустою, то і вся область АВ є непустою). Отже, АВ ¹ Æ. Правильність модусу доведена.

Аналізуючи цей приклад, слід мати на увазі таку обставину. Немає ніякої суперечності у тому, що в силу інформації, яку містить в собі один із засновків (аМВ º МВ¹ ¹ Æ), поле АМВ¹ заштриховується, тобто визнається пустим, а в силу інформації, яку дає другий засновок (іМА¹ = МА ¹ Æ), це саме поле позначається точкою. Справді, риска, що з’єднує дві точки і зображена в силу інформації, що її містить засновок МА¹Æ, показує тільки те, що пустим не є ціле, складене з АМВ¹ і АМВ, а для того, щоб ціле було непустим, досить, щоб хоч одна його частина була непустою (у даному випадку АМВ).

Рис. 15

Приклад 3. Перевірити логічну правильність силогізму, який має такий модус:

аАМ АМ¹ = Æ

аВМВМ¹ = Æ

іАВ АВ ¹ Æ

Заштрихувавши області АМ¹ та ВМ¹, як того вимагають засновки силогізму, бачимо, що з діаграми не випливає пустота області АВ. У висновку ж говориться про те, що ця область не є пустою. Отже, даний модус силогізму є неправильним.

Рис. 16

Приклад 4. Перевірити логічну правильність силогізму:

Ти не я. еАМ АМ = Æ

Я — людина. аМВМВ¹ = Æ

Ти не людина еАВ АВ = Æ

Діаграма показує, що область АВ насправді не є пустою. Отже, силогізм неправильний.

Рис. 17

Приклад 5. Перевірити силогізм:

Всі алмази горять. аМВ МВ¹ = Æ

Всі алмази камені.аМАМА¹ = Æ

Деякі камені горять. іАВ АВ ¹ Æ

Відношення між обсягами класів, що входять до складу цього силогізму, показано на рис. 17. Діаграма не містить в собі інформації, на підставі якої можна було б сказати щось визначене (певне) щодо співвідношення класів А і В. Зокрема, на рисунку не вбачається непустота АВ (АВ ¹ Æ), як цього вимагає висновок силогізму.

Рис. 18

Про те, що в даному силогізмі висновок з необхідністю не випливає із засновків, свідчить і діаграма, побудована за допомогою кіл Ейлера (рис. 18). Висновок у цьому силогізмі можливий лише за умови, що клас М (він на діаграмі Ейлера заштрихований) непустий.

Якщо ж клас М виявиться пустим, то ніякого висновку про зв’язок А і В не можна буде зробити, бо тоді класи А і В виявляться не зв’язаними між собою. Оскільки сучасна формальна логіка ґрунтується на визнанні існування пустих класів, то силогізм, що розглядається, є хибним виводом.

Таким чином, модус Darapti (аіі) а МА

а МВ

і АВ

не є правилом виводу, або, що те саме, імплікація аМА Ù аМВ ® іАВ не є логічним законом.

Зауважимо при цьому, що люди, не знайомі з сучасною логікою, виходячи з так званого здорового глузду, вважають зазначений силогізм цілком правильним. Справді, у практиці повсякденного мислення ми часто ведемо міркування за схемою прикладу 5 і ніколи не приходимо до суперечності. Річ у тім, що у практиці буденного мислення ми, як правило, не маємо справи з пустими класами і формулюємо наші судження тільки відносно непустих класів. За цієї умови схема 5 стає правилом виводу. Справді, при припущенні М ¹ 0 (тобто при припущенні третього засновку «Алмази горять») ми одержуємо ВА ¹0. Особливо це чітко видно з діаграми Ейлера (рис. 18). Але те, що правильно у повсякденному мисленні, не завжди правильно у науковому мисленні, а сучасна логіка перш за все обслуговує мислення наукове.

Це саме можна сказати і про всі інші модуси, у яких засновки — загальні судження, а висновки — часткові. До них належать модуси Felapton (ІІІ фігура), Bramantip і Fesapo (IV фігура).

Тому чотири схеми силогізму:

ІІІ фігура аМВ еМВ IV фігура аВМ еВМ

аМА аМАаМАаМА

іАВ оАВ іАВ оАВ

сучасною логікою і математикою не приймаються за прави-
ла умовиводу, тоді як у практиці буденного мислення (тобто
за припущення непустоти класу М) вони є правилами виво-
ду. Справедливість сказаного випливає з таких діаграм Венна і Ейлера:

Felapton Рис. 19 Рис. 19а

еМВ МВ = Æ

аМАМА¹ = Æ

оАВ АВ¹ ¹ Æ

Bramantip   Рис. 20 Рис. 20а

аВМ ВМ¹ = Æ

аМАМА¹ = Æ

іАВ АВ ¹ Æ

Fеsaro Рис. 21 Рис. 21а

еВМ ВМ = Æ

аМАМА¹ = Æ

оАВ АВ¹ ¹ Æ

З наведених діаграм Венна видно, що жоден з трьох висновків не випливає з діаграм (модус Darapti був пояснений вище). Діаграми Ейлера показують, що при непустоті класу М висновки за цими модусами є правомірними. При пустоті ж класу М висновки з цих засновків не випливають. Останнє вимагає певних пояснень до наведених діаграм Ейлера.

Рис. 22

Рис. 19а. Клас М (він заштрихований скісними і горизонтальними лініями) включається в клас А (цей клас заштрихований горизонтальними лініями) і виключається з класу В. При непустому М існують предмети, які належать до класу А і не належать до класу В (це всі предмети класу М), тобто АВ¹ ¹ Æ. Коли ж клас М буде пустим, то за цієї обставини всі предмети класу А включатимуться в клас В (це та частина класу А, яка заштрихована тільки горизонтальними лініями), тобто АВ¹ = Æ. Таким чином, навіть за допомогою діаграм Ейлера можна графічно показати, що при М = Æ у модусі третьої фігури еао висновок (АВ¹ = Æ) не є логічним наслідком із засновків.

Рис. 19а в силу специфічності модусу побудований так, що клас М зображений не у вигляді кола, як це звичайно робиться, а у вигляді сегмента. Дане співвідношення обсягів термінів (класів) природніше передається прямокутниками (рис. 22).

Рис. 20а. При пустому М (М = Æ) клас В виявиться також пустим, оскільки він є частиною класу М. Звідси ясно, що класи А і В не матимуть спільних елементів (АВ = Æ), інакше кажучи, судження «Деякі А є В» виявляться хибними. Отже, при визнанні існування непустих класів логічна неправильність модусу ааі четвертої фігури випливає також з діаграми Ейлера.

Рис. 21а. Все сказане про рис. 19а стосується також рис. 21а., оскільки модуси даних силогізмів (еао) та їхні графічні зображення такі самі.

Розглянутий матеріал дає підстави твердити, що діаграми Венна можуть бути використані як ефективний спосіб відбору логічно правильних модусів категоричного силогізму як при звичайному його аналізі, так і в комп’ютерному варіанті.

5.6. Розв’язання задач на категоричний
силогізм за допомогою антилогізму

Зручним і швидким способом розв’язання задач на категоричний силогізм є антилогізм. Цей спосіб розв’язання задач особливо ефективний за допомогою комп’ютера, оскільки вимагає мінімум даних і команд.

Антилогізм — це формула логіки, яка виражає несумісність засновків категоричного силогізму із запереченням його висновку. Антилогізм заснований на властивості логічного слідування, яке полягає в тому, що висновок (наслідок) не може бути хибним за істинності засновків.

1) Антилогізми складаються з двох рівностей і однієї нерівності (з двох загальних і одного часткового судження).

2) У рівностях міститься одна і тільки одна спільна буква, взята в одній рівності зі штрихом, а в другій — без штриха (тобто у загальних судженнях повинно зустрічатися одне й те саме поняття, взяте в одному судженні у ствердній формі, а в другій — у заперечній).

3) Кожна з двох останніх букв в обох своїх входженнях (во-
на входить у нерівність і в одну із рівностей) повинна бути штрихованою або нештрихованою (тобто кожне з двох останніх по-
нять повинно всюди братися або в ствердній, або в заперечній формі).

Антилогізми, які мають усі зазначені властивості, називаються правильними, а ті, що не мають хоча б однієї з них, — неправильними.

Проаналізуємо кілька категоричних силогізмів і ентимем за допомогою антилогізму. Зауважимо, що для спрощення операції переведення суб’єктно-предикатної форми запису категоричних суджень на мову класів («пусте — непусте») можна не позначати менший термін символом А, а більший — символом В, а передавати їх прийнятими для категоричних силогізмів символами S і Р.

Перевіримо за допомогою антилогізму логічну правильність категоричного силогізму:

Будь-яка речовина має вагу.

Повітря має вагу.

Повітря — речовина.

Спочатку необхідно визначити тип суджень, що входять до цього силогізму, встановити модус і склад термінів силогізму. Тоді силогізм набуде такого вигляду:

Р М

(А) Будь-яка речовина має вагу.

S М

(А) Повітря має вагу.

S Р

(А) Повітря — речовина.

Тепер запишемо схему цього силогізму мовою класів («пусте — непусте»):

(А) Всі Р є М º а РМ¹ = Æ

(А) Всі S є М º а SМ¹ = Æ

(А) Будь-яке S є Р º а SР¹ = ÆÆ

Для побудови антилогізму необхідно записати силогізм у формалізованому вигляді. Для цього засновки з’єднуються кон’юнк­тивно, а висновок — приєднується за допомогою знака (символу) імплікації:

(РМ¹ = Æ) Ù (SМ¹ = Æ) ® (SР¹ = Æ)

До цього силогізму побудуємо антилогізм, який має бути запереченням висновку із наведених засновків за допомогою символу кон’юнкції, а знак висновку поміняти на протилежний, тобто якщо у висновку стоїть знак нерівності, то його необхідно замінити знаком рівності. У нашому випадку антилогізм набере вигляду:

(РМ¹ = Æ) Ù (SМ¹ = Æ) Ù (SР¹ ¹ Æ)

Як бачимо, цей антилогізм складається з двох рівностей і однієї нерівності. Отже, перше правило антилогізму виконується. Але два інші правила порушені: у рівностях спільна буква М обидва рази взята штрихованою, а буква Р у першому входженні взята без штриха, а в другому — зі штрихом (за правилом вона має братися однаково в обох своїх входженнях). Стосовно S правило викона-
но. Таким чином, антилогізм показав, що цей силогізм є непра-
вильним.

Як бачимо, аналіз силогізму за допомогою антилогізму зручний тим, що при цьому немає потреби встановлювати розподіленість термінів, фігуру силогізму, перевіряти особливі правила фігур і
загальні правила силогізму, а також будувати діаграми Ейлера чи Венна.

Методом антилогізму перевіримо ще такий силогізм: «Часом гра його хороша, бо часом він грає щиро, а щира гра завжди хороша». Після знаходження засновків і висновку силогізм набуває такої нормальної форми:

М Р

(А) Щира гра завжди хороша.

S М

(І) Часом він щиро грає.

S Р

(І) Часом гра його хороша.

Запишемо цей силогізм мовою класів:

аМР¹ = Æ

іSМ ¹ Æ

іSР ¹ Æ

Тоді антилогізм набуде такого вигляду:

(МР¹ = Æ) Ù (SМ ¹ Æ) Ù (SР = Æ).

Як бачимо, всі три правила антилогізму тут збережено (у ньому є дві рівності і одна нерівність; у рівностях Р один раз взяте зі штрихом, другий — без штриха; дві інші букви — М і S — в обох входженнях взяті однаково). Отже, силогізм правильний.

Методом антилогізму перевіримо логічну правильність ен-
тимем:

1) «Сьогодні барометр падає, отже, сьогодні погода зіпсується»;

2) «У нього немає температури, значить, він не хворий».

1) Відновлена у повний силогізм ентимема набуде вигляду:

М Р

(А) При падінні барометра погода зіпсується.

S M

(А) Сьогодні барометр падає.

S P

(А) Сьогодні погода зіпсується.

Запишемо відновлений силогізм мовою класів:

аМР¹ = Æ

аSМ¹ = Æ

аSР¹ = Æ

Утворимо з цієї схеми антилогізм:

(МР¹ = Æ) Ù (SМ¹ = Æ) Ù (SР¹ ¹ Æ)

Як бачимо, що всі три правила антилогізму тут виконуються, отже, антимема правильна.

2) Відновлена у повний силогізм ентимема матиме вигляд:

М Р

(А) Усі, хто має температуру, хворі.

S M

(Е) У нього немає температури.

S P

(Е) Він не хворий.

Мовою класів вона запишеться так:

аМР¹ = Æ

eSМ = Æ

eSР = Æ

Антилогізм цієї ентимеми, відновленої у силогізм, такий:

(МР¹ = Æ) Ù (SМ = Æ) Ù (SР ¹ Æ)

Аналіз антилогізму показує, що в рівностях М обидва рази взято без штриха, що є порушенням другого правила антилогізму; буква Р в одному входженні взята зі штрихом, а в другому — без штриха, що є порушенням третього правила антилогізму. Отже, ентимема, що розглядається, є неправильною.

Розглянуті приклади застосування методу антилогізму для аналізу категоричних силогізмів і ентимем наочно довели, що цей метод зручний тим, що при його використанні немає потреби встановлювати розподіленість термінів і фігуру силогізму, перевіряти особливе правило фігури й загальні правила силогізму, будувати діаграми Ейлера чи Венна.

ДОТЕПНІ ЗАДАЧІ З ЛОГІКИ

Не нашли, что искали? Воспользуйтесь поиском: