ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сложное движение точки
В ряде случаев при решении задач механики оказывается целесообразным (а иногда и необходимым) рассматривать движение точки (или тела) одновременно в двух системах отсчёта, из которых одна остается условно неподвижной, а другая определённым образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называется сложным. Например, шар, катящийся по палубе движущегося парохода, можно считать совершающим по отношению к берегу сложное движение, состоящее из качения по отношению к палубе, с которой связана подвижная система отсчёта OXYZ, и движения вместе с палубой по отношению к берегу, с которым связана неподвижная система отсчёта O1X1Y1Z1. Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых. Возможность разложения сложного движения точки на более простые путём введения дополнительной (подвижной) системы отсчёта широко используется в кинематических и динамических расчётах.
Введем следующие понятия, применяемые в сложном движении точки.
Движение точки по отношению к неподвижной системе отсчёта O1X1Y1Z1 называется абсолютным и характеризуется абсолютной скоростью V и абсолютным ускорением а (рис. 2.41).
Положение точки на траектории абсолютного движения определяется тремя зависящими от времени координатами, которые называются уравнениями абсолютного движения:
X1 = f1(t);
Y1 = f2(t);
Z1 = f3(t).
Зная уравнения абсолютного движения, несложно определить абсолютные скорость V и ускорение а точки по формулам:
;
cos(V, i) 
cos(V, j) 
cos(V, k) 
а = 
cos(а, i 1) = 
/ а; cos(а, j 1) = 
/ а; cos(а, k 1) = 
/ а.
Движение точки по отношению к подвижной системе отсчёта OXYZ называется относительным движением и характеризуется относительной скоростью Vr и относительным ускорением ar (рис. 2.42).
Положение точки на траектории относительного движения определяется тремя зависящими от времени координатами, которые называют уравнениями относительного движения:
X = f4(t);
Y = f5(t);
Z = f6(t).
Зная уравнения относительного движения, несложно определить относительную скорость V r и относительное ускорение a r по формулам:
cos(V r, i)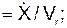 
cos(V r, j) 
cos(V r, k) 
a r =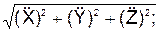 
cos(a r, i) = 
/ a r; cos(a r, j) = 
/ a r;
cos(a r, k) = 
/ a r.
Пусть координаты точки в подвижной системе отсчёта OXYZ постоянны: X = C1 = const; Y = C2 = const; Z = C3 = const. При этом условии точка неподвижна относительно ПСО, которая совершает движение относительно НСО. Движение этой точки вместе с подвижной системой отсчёта OXYZ относительно неподвижной системы отсчёта O1X1Y1Z1 называется переносным движением, которое характеризуется переносной скоростью V e и переносным ускорением a e(рис. 2.43).
Положение точки на траектории переносного движения определяется тремя зависящими от времени координатами, которые называют уравнениями переносного движения:
По известным уравнениям переносного движения находится переносная скорость V e и переносное ускорение a e.
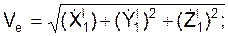
cos(V e, i) = 
/ Ve;
cos(V e, j) = 
/ Ve;
cos(V e, k) = 
/ Ve;
a e = 
cos(a e, i) = 
/ a e;
cos(a e, j) =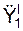 
/ a e;
cos(a e, k) = 
/ a e.
На рис. 2.44 приведен пример сложного движения точки.
В неподвижной системе отсчёта O1X1Y1Z1 флажок вращается относительно оси O1Y1 с переносной угловой скоростью 
. На флажке закреплена подвижная система отсчёта OXYZ, которая вращается с флажком относительно оси O1Y1. На флажке выполнен канал, по которому движется точка М с относительной скоростью V r.
Траектория относительного движения – прямая линия ОА на флажке. Уравнение относительного движения задано Sr = f(t).
Для определения траектории переносного движения поступают следующим образом. Задают время t1 и определяют положение точки М на траектории относительного движения. Sr(t1) = const. Зафиксированная на траектории относительного движения точка М в момент времени t1 вместе с флажком описывает в неподвижной системе отсчёта O1X1Y1Z1 окружность радиусом МК. Эта окружность является траекторией переносного вращения. Необходимо отметить, что в другой момент времени t2 координата точки М на траектории относительного движения Sr(t2) будут иметь другое значение и, следовательно, траекторией переносного движения будет окружность с другим радиусом.
Если в каждый момент времени складывать относительное и переносное движения, то получим абсолютное движение. В рассматриваемом примере траекторией абсолютного движения является винтовая линия, сформированная на конусе, образованном прямой ОА на флажке при её вращении относительно оси O1Y1.
Сложение скоростей
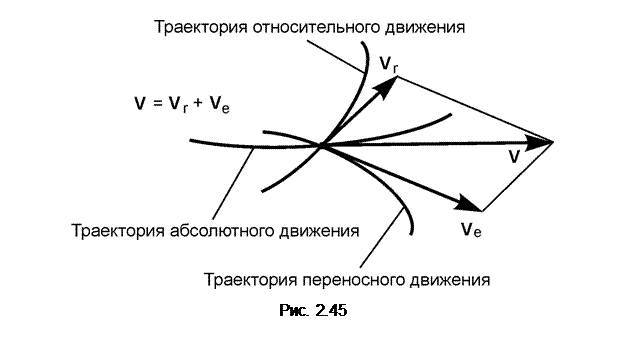
Рассматривается сложное движение точки на плоскости (рис. 2.45).
Поскольку абсолютное движение представляет собой сумму относительного и переносного движений, то справедлива следующая теорема: при сложном движении абсолютная скорость V точки равна геометрической сумме относительной Vr и переносной Ve скоростей:
V = V r + V e.
Построенная на рис. 2.45 фигура называется параллелограммом скоростей. Модуль абсолютной скорости находится по формуле
Не нашли, что искали? Воспользуйтесь поиском: