Формула полной вероятности и формулы Байеса

Пусть наступление случайного события А влечёт наступление одного из попарно несовместных случайных событий Н ₁, Н ₂,…, Н_n, и Р (Н_i) > 0, i = 1,…, n, тогда справедлива формула полной вероятности:

Р (А) = Р (Н ₁) Р (А ï Н ₁) + Р (Н ₂) Р (А ï Н ₂) +… + Р (Н _n) Р (А ï Н _n),

а также формулы Байеса:

Р (Н_i ï А) = , i = 1, 2, …, n,

в которых Р (А) вычисляется по формуле полной вероятности.

Пример. В ящике пять деталей, изготовленных на заводе №1, и четыре детали, изготовленных на заводе №2. Каждая деталь завода №1 не имеет дефектов с вероятностью 0,8, а каждая деталь завода №2 − с вероятностью 0,9. Наугад взятая деталь не имеет дефектов. Найти вероятность того, что взятая деталь изготовлена на заводе №1.

Решение. Рассмотрим случайные события

А = {взятая деталь не имеет дефектов},

Н ₁ = {взятая деталь изготовлена на заводе №1},

Н ₂ = {взятая деталь изготовлена на заводе №2}.

Нужно найти вероятность того, что взятая деталь изготовлена на заводе №1 при условии, что она не имеет дефектов, т.е. найти условную вероятность Р (Н ₁| А).

Случайные события Н ₁ и Н ₂ несовместны и образуют полную группу, т.е. в случайном эксперименте (наугад берут деталь) всегда наступает одно из этих событий. Значит, условную вероятность Р (Н ₁| А) можно найти по формуле Байеса, а вероятность случайного события А по формуле полной вероятности

.

Используя классическое определение вероятности, найдем

, .

Из условия задачи и . Следовательно,

, .

Ответ: .

К задачам 431 − 450.

Случайная величина Х − это функция, определенная на множестве элементарных исходов Ω случайного эксперимента, и принимающая значения во множестве действительных чисел.

.

Если случайная величина, имеет конечное или счетное число значений, то она называется дискретной. Чтобы задать закон распределения дискретной случайной величины Х, нужно указать все значения х_i этой случайной величины и вероятности р_i = Р (Х = х_i) наступления случайных событий { Х = х_i }, i = 1, 2,3, … Если все эти вероятности заданы правильно, то их сумма равна 1.

Пусть случайная величина Х имеет конечное число значений х₁, х₂, …, х_n и Р (Х = х_i) = р_i, i = 1, 2, …, n, тогда математическим ожиданием случайной величины Х называется число, обозначаемое М (Х) и определяемое формулой

.

Математическое ожидание случайной величины Х определяет центр, около которого расположены значения этой величины. Разброс значений относительно этого центра характеризуется другой числовой характеристикой, которая называется дисперсией и определяется формулой

.

Для вычисления дисперсии можно использовать формулу

,

где число называется вторым моментом случайной величины Х. Значит, дисперсия случайной величины равна разности второго момента и квадрата математического ожидания этой случайной величины.

Пример. На одной грани кубика написано число 3, на двух − число 2 и на трех − число 1. Кубик бросили три раза. Найти математическое ожидание и дисперсию суммы выпавших чисел.

Решение. Пусть случайная величина Х_i − это число, выпавшее при i -ом бросании кубика, i = 1, 2, 3, а случайная величина Х − это сумма выпавших чисел. Тогда . Найдем закон распределения случайной величины Х_i. Случайная величина Х_i может принимать значения 1, 2 и 3. Используя классическое определение вероятности, найдем вероятности

.

Следовательно,

,

,

, i = 1, 2, 3.

Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин, поэтому

.

Случайные величины Х₁, Х₂, Х₃ связаны с независимыми экспериментами, поэтому эти случайные величины являются независимыми, а дисперсия суммы независимых случайных величин равна сумме дисперсий этих случайных величин. Используя это свойство дисперсии, получим, что

.

Ответ: .

Функцией распределения случайной величины Х называется функция y = F (x) такая, что F (x) = P (X < x) для всех .

Случайная величина Х называется абсолютно непрерывной, если ее функция распределения y = F (x) дифференцируема во всех точках за исключением, быть может, конечного числа точек, при этом функция называется плотностью распределения случайной величины Х.

Пусть y = f (x) − плотность распределения абсолютно непрерывной случайной величины Х, тогда

1) ;

2) − функция распределения случайной величины Х;

3) − математическое ожидание случайной величины Х при условии, что несобственный интеграл сходится;

4) 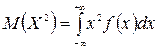− второй момент случайной величины Х при условии, что несобственный интеграл сходится;

5) − дисперсия случайной величины Х;

6) любое решение уравнения , где y = F (x) − функция распределения случайной величины Х, является медианой случайной величины Х и обозначается Ме (Х).

Пример. Дана плотность распределения

случайной величины Х. Найти неизвестный параметр с, а также функцию распределения, медиану, математическое ожидание и дисперсию случайной величины Х.

Решение. Найдем неизвестный параметр с из условия .

Поскольку плотность распределения должна быть неотрицательной, то .

Найдем функцию распределения. Для этого рассмотрим несколько случаев.

1) ;

2) ;

3) ;

4) .

Найдем медиану. Если или , то уравнение решений не имеет. Пусть , тогда ,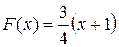

Следовательно, .

.

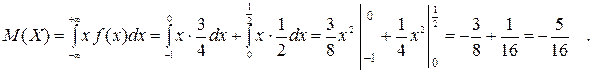
Ответ: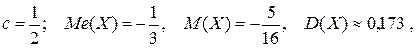

К задачам 451 − 460. Случайная величина Х имеет биномиальное распределение с параметрами и , если ее значения 0, 1, 2, …, n и вероятность вычисляется по формуле Бернулли:

, k = 0, 1, 2, …, n, где q = 1 − p.

Случайную величину Х, имеющую биномиальное распределение с параметрами р и n, можно рассматривать как число наступлений случайного события А в n независимых испытаниях, в каждом из которых случайное событие А наступает с вероятностью р и не наступает с вероятностью q = 1 − р.

Если случайная величина Х имеет биномиальное распределение с параметрами p и n, где , то при большом числе испытаний n и малой вероятности p для вычисления вероятности применяется формула Пуассона

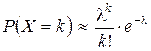, где .

Абсолютная погрешность формулы Пуассона не превосходит . Если это число не является малым, то для вычисления вероятности нужно использовать локальную теорему Муавра − Лапласа, согласно которой

,

где − плотность распределения случайной величины, имеющей стандартное нормальное распределение.

Интегральная теорема Муавра − Лапласа дает формулу для приближенного вычисления вероятности :

,

где , и − функция Лапласа.

Заметим, что функция Лапласа является нечетной, т.е. 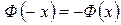для любого х.

Функция Лапласа табулирована. Укажем ее некоторые значения.

		1,64	0,4495
0,4	0,1554	1,65	0,4505
0,6	0,2257	1,84	0,4671
0,8	0,2881	1,96	0,4750
	0,3413	2,5	0,4938
1,5	0,4332		0,499968

Если , то .

Пример. Найти вероятность того, что из 100 проверенных изделий а) 90 изделий, б) не более 95 изделий окажутся изделиями первого сорта, если каждое проверяемое изделие является первосортным с вероятностью 0,9.

Решение. Пусть Х − число изделий первого сорта из 100 проверенных изделий. Случайная величина Х имеет биномиальное распределение с параметрами и .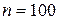

а) Для нахождения вероятности используем локальную теорему Муавра-Лапласа

,

где , , , .

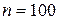Следовательно, 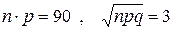и .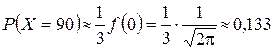

б) Для нахождения вероятности используем интегральную теорему Муавра-Лапласа.

,

где , , , .

Следовательно, .

Ответ: а) 0,133; б) 0,4772.

Не нашли, что искали? Воспользуйтесь поиском: