
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Шаг рейки p - расстояние между одноименными точками двух соседних зубьев. Шаг складывается из толщины зуба s и ширины впадины e.
Единственная прямая исходного контура, на которой толщина зуба равна ширине впадины, называется делительной прямой рейки., остальные прямые называются начальными прямыми рейки. Шаг зубьев рейки p = π m, толщина зкуба s = e = π m / 2.
Делительная прямая рейки делит зуб на головку и ножку. Высота головки – ha = 1.25 m, высота ножки – hf = m, высота всего зуба – h = 2.25 m. Головка закруглена радиусом ρ = 0.38 m.
Инструмент изготавливается по производящему исходному контуру, отличающемуся от теоретического исходного контура тем, что впадина сделана глубже на 0.25 m и закруглена так же как головка. Это сделано для того, чтобы впадина инструмента не касалась заготовки. Следовательно впадина не участвует в нарезании зуба. Зуб нарезают прямолинейные боковые кромки и скругленная вершина зуба. Рейку можно рассматривать как зубчатое колесо бесконечно большого радиуса. В этом случае эвольвента превращается в прямую линию.
5.9. Элементы нулевого зубчатого колеса
У нарезаемого зубчатого колеса на различных окружностях различный шаг зубьев. Та единственная окружность, на которой шаг зубьев равен шагу зубьев рейки, называется делительной. Шаг измеряется по дуге окружности. Ее длина l = p z = π d, откуда следует d = pz / π = mz. Исходя из этой формулы, можно дать определение делительной окружности как окружности, на которой модуль зуба равен модулю рейки.
Инструмент можно устанавливать на различном расстоянии от центра заготовки. Рассмотрим частный случай, когда делительная прямая касается делительной окружности. Нарезаемое таким образом колесо называется нулевым. Основание для такого названия выяснится в дальнейшем.

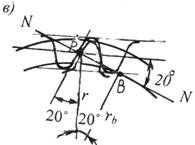
Рис. 5.10. Изготовление колес без смещения
Поскольку шаги на делительной окружности и на делительной прямой одинаковы, эти линии катятся друг по другу без скольжения. Толщина зуба делительной прямой рейки воспроизводится без искажения на делительной окружности как ширина впадины колеса. Тогда s = π m / 2, аналогично определяется ширина впадины. Остальные размеры колеса также определены размерами рейки:
h= 2.25 m;
ha = m;
hf = 1.25 m;
da = m (z + 2);
df = m (z – 2.5).
Прямолинейные режущие кромки нарезают эвольвентную часть зуба, которая идет до основной окружности. Для определения диаметра основной окружности проведем через точку Р общую нормаль N – N. Она проходит под углом 20˚ к делительной прямой. Основная окружность касается общей нормали. Из построения на рис. 5.10 следует, что db = m z cos 20˚.
Из рассмотрения рис.5.10 следует еще один важный вывод, используемый в дальнейшем: угол профиля эвольвенты в точке, лежащей на делительной окружности, равен углу наклона боковой линии рейки, т.е. 20˚.
5.10. Нарезание зубчатых колес со смещением
Рассмотрим случай, когда делительная прямая не касается делительной окружности и смещена от нее в направлении от центра колеса на некоторое расстояние X (рис.5.11). Это расстояние называется смещением и выражается через модуль и коэффициент смещения x
X = x m.
Делительная окружность касается некоторой начальной прямой. Поскольку на начальной прямой шаг равен шагу на делительной окружности, то можно считать, что начальная прямая перекатывается по делительной окружности без скольжения и отпечатывает на ней толщину зуба и ширину впадины.

Рис. 5.11. Изготовление колес со смещением
Из построения на рис.5.11 следует, что толщина зуба на делительной окружности
s = π m / 2 + 2 mx tg 20°,
ширина впадины
e = π m / 2 - 2 mx tg 20˚,
диаметры окружностей вершин и впадин
da = m (z – 2.5 + 2x),
df = m (z – 2.5 + 2x).
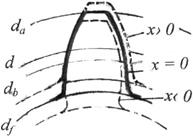
Рис. 5.12.Влияние смещения на профиль зуба
Рассмотренный случай называется положительным смещением. Коэффициент смещения х здесь считается положительным. Если сместить рейку в направлении к центру колеса, то ее делительная прямая пересечет делительную окружность (рис.5.12). Такой случай называется отрицательным смещением. Нетрудно убедиться, что для него справедливы все выведенные выше формулы, если принять в них коэффициент смещения с отрицательным знаком. Если положить х = 0, то получим формулы для нулевого колеса.
5.11. Влияние смещения на профиль зуба
На рис.5.12 представлены профили зубьев колес с одним модулем и числом зубьев, но с различными коэффициентами смещения. Из сравнения их следуют выводы:
1. Диаметры делительной d и основной db окружностей не изменяются.
2. При х > 0 диаметры вершин и впадин увеличиваются
3. При х > 0 толщина зуба s увеличивается, ширина впадины уменьшается, ножка зуба становится толще и короче, что увеличивает изгибную прочность зуба.
4. Смещение не изменяет делительного и основного шага, поэтому зацепление колес с различным смещением происходит нормально
5. При х > 0 профиль зуба располагается на участках с меньшей кривизной эвольвенты, что увеличивает контактную прочность зуба
6. При х > 0 толщина зуба по окружности вершин уменьшается
При отрицательном смещении происходят изменения в противоположном направлении и зуб несколько ослабляется. Так как колесо обычно прочнее шестерни, для создания равнопрочной передачи шестерне делают положительное смещение, а колесу – отрицательное, Правильно подобрав смещение, можно значительно повысить прочность передачи.
5.12. Подрезание, интерференция, заострение
Подрезание проявляется в утончении ножки зуба и приводит к уменьшению изгибной прочности зуба и, кроме того, в связи с сокращением эвольвентного участка, к нарушению закона зацепления на части профиля.
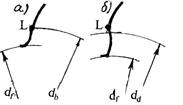
Рис. 5.13. Подрезание ножки зуба
Боковой профиль зуба состоит из главной части и переходной кривой, разделенных граничной точкой L (рис.5.13). Положение точки L при заданном числе зубьев зависит от коэффициента смещения. Коэффициент смещения, при котором точка L лежит на основной окружности, называется коэффициентом смещения. Если x < xmin, переходная кривая пересечет главный профиль дальше основной окружности и часть эвольвенты будет срезана, зуб окажется подрезанным (рис. 5.13).

Рис. 5.14. К расчету минимального смещения
Для установления зависимости коэффициента смещения х от числа зубьев, рассмотрим схему станочного зацепления при нарезании нулевого колеса (рис.5.14). Установлено, что подрезание возникает, если начальная прямая, проходящая через конец прямолинейной части рейки, заходит за точку касания производящей прямой с основной окружностью – точку А. Для устранения подрезания дадим рейке положительное смещение такое, чтобы точки а и в совпали. Рассмотрим вытекающее из геометрических построений соотношения. Из треугольника АТО следует OT = AO cos 20˚, из треугольника OPA - AO = OP cos 20˚. Тогда OT OP cos2 20˚. С другой стороны ОТ = ОР – ТР, где ОР = mz / 2, TP = m – xm. Приравняв обе формулы, получим ОР cos2 20˚ = OP – TP. После соответствующих подстановок и преобразований окончательно получим
X = (17 – z)/ 17. (5.1)
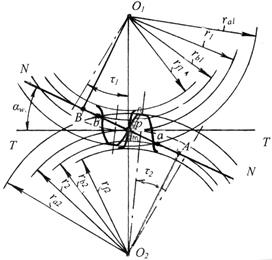
Рис. 5.15. Картина зацепления
Коэффициент смещения, определенный по формуле (5.1), представляет минимальный коэффициент смещения, при котором отсутствует подрезание. Минимальное число зубьев, свободное от подрезания, равно 17 – для него х = 0. Все колеса с числом зубьев меньше 17 обычно изготавливаются со смещением. Впрочем, небольшое подрезание допускается и даже полезно с точки зрения уменьшения кромочных ударов при зацеплении. При рассмотрении картины зацепления может обнаружиться, что главный профиль головки зуба, сопрягаясь с переходной кривой, внедряется в нее. Такое явление при изготовлении колес приводит к рассмотренному выше подрезанию, а при их зацеплении – к непроворачиваемости и поломке зубьев. Такое явление носит название интерференции. Интерференции не будет, если эвольвентный профиль сопрягается только с эвольвентным, в теории зацепления установлены условия, при которых будет отсутствовать интерференция. Наиболее часто интерференция возникает при внутреннем зацеплении. Необходимо проектировать внутреннее зацепление так, чтобы разница чисел зубьев колес была не менее 7 – 8.
Толщина зуба по окружности вершин зависит от смещения, с увеличением смещения она уменьшается. Может возникнуть заострение зуба, когда толщина зуба по окружности вершин sa = 0. Заострение нежелательно из –за недостаточной прочности зуба – вершина заостренного зуба совершенно неспособна воспринимать нагрузку. Обычно принимают sa > 0.25m – для кинематических передач и sa > 0.4m – для силовых передач. Толщину зуба по окружности вершин можно проверить по приводимой далее формуле.
5.13. Построение картины зацепления
Для построения картины зацепления необходимо по известным формулам определить параметры зубчатых колес: d1, d2, da1, da2, df1, df2, db1, db2, s1, s2, p. Межосевое расстояние вычисляется по формуле:
аW = (dW! + dW2) / 2. (5.2)
В частном случае aW = a, где а – делительное межосевое расстояние, a = (d1 + d2) / 2. Отложим межосевое расстояние aW, отметим центры вращения колес О1 и О2, построим для каждого колеса окружности вершин, окружность впадин, делительную окружность, основную окружность (рис.5.15).
Проведем общую нормаль касательно к основным окружностям, Она пересечет межосевое расстояние в точке Р – полюсе зацепления, через который проходят начальные окружности. Используя общую нормаль как производящую прямую, построим эвольвентный участок профиля зуба первого колеса.
Способ построения эвольвенты описан ранее. Переходная кривая условно оформляется как радиальная прямая, сопряженная с окружностью впадин галтелью радиусом ρ = 0.4 m. Отложим половину толщины зуба по делительной окружности и проведем ось симметрии зуба. Для этого удобно воспользоваться шаблоном. Откладывая угловой шаг τ1 = 2π / z1 и используя шаблон зуба, строим 3 – 4 зуба. Точно так же строятся зубья второго колеса.
На картине зацепления можно отметить следующие элементы:
АВ – теоретическая линия зацепления, геометрическое место точек касания профилей зубьев;
ав – активная линия зацепления, часть теоретической линии, ограниченная окружностями вершин;
mn - активная часть профиля зуба, непосредственно участвующая в зацеплении. Для ее определения нужно перенести точку, а радиусом оа на профиль зуба;
αW - угол зацепления, угол между линией зацепления и общей касательной Т – Т. Угол зацепления равен углу профиля эвольвенты αy в точке, лежащей на начальной окружности.
5.14. Коэффициент перекрытия
Одной из важнейших качественных характеристик зацепления является коэффициент перекрытия. Он характеризует плавность зацепления колес. Коэффициент перекрытия равен отношению угла перекрытия φα к угловому шагу τ:
εα= φα / τ. (5.3)

Рис. 5.16. К определению коэффициента перекрытия
Угол перекрытия есть угол поворота зубчатого колеса от положения входа зуба в зацепление до положения выхода из зацепления. Его можно определить, рассмотрев два положения зуба – в момент входа и в момент выхода из зацепления (рис. 5.16).
Угол перекрытия должен быть больше углового шага. Благодаря этому первая пара зубьев еще не успевает разомкнуться (придти в точку в) как вторая пара зубьев входит в зацепление. Таким образом, существуют периоды двухпарного зацепления. Это обеспечивает непрерывность зацепления. Чем больше εα, тем плавнее работает передача.
Установим зависимость εα от параметров зацепляющихся колес. Умножим числитель и знаменатель формулы (5.3) на rb - радиус основной окружности. С учетом 4 – го свойства эвольвенты φα rb1 = ab, кроме того, τ1 rb1 = pb - шаг зубьев по основной окружности, следовательно, получим формулу:
εα = ав / pb. (5.4)
Формулу (5.4) можно использовать, если построена картина зацепления, на которой можно замерить длину активной линии зацепления ав.
Для получения аналитической зависимости следует представить длину активной линии зацепления в функции от параметров колес.
Из построения на рис.5.16 следует:
Ав = Рв = аР;
Рв = Ав – рА;
АР = Ва – РВ.
Из треугольников О1Ав и О1АР следует:
ав = rb1 tg αa1; РА = rb1 tg αW.
Из треугольников О2Ва и О2ВР следует
Ba = rb2 tg αa2; PB = rb2 tg αW.
Произведя подстановку полученных выражений в формулу (5.4) и выполнив необходимые преобразования, получим:
εα = (z1 (tg αa1 - tg αW) + z2 (tg αa2 – tg αW)) / 2π.
Здесь
аa1 = arccos (db1 / da1); αa2 = arccos (db2/ da2).
Как вычисляется αW будет показано в дальнейшем.
Коэффициент перекрытия для прямозубых колес должен находиться в пределах 1.2 < εα < 1.98.
5.15. Толщина зуба на окружности произвольного радиуса
Определим толщину зуба sy на окружности диаметра dy. Из построений на рис. 5.17 следует:
Sy = ψy dy ; (5.5)
Ψy = ψ + θ - θy,
где θ = inv 20˚, θy = inv αy.
Для определения αy рассмотрим треугольник ОВY
αy = arccos (db / dy).
Угол ψ находится из соотношения ψ = s/d, где s – толщина зуба на делительной окружности. Используя формулу (5.5), получим
ψ = π/ 2z + 2 x tg 20˚/ z.
Тогда
ψy = π/ 2z + 2x tg20˚ + inv20˚ - inv αy.
Толщина зуба и ширина впадины определяются из следующих выражений
sy = dy (π /2z + 2x tg20˚ + inv20˚ - invαy);
еy = dy(π / 2z – 2x tg20˚ - inv20˚ + inv αy).
5.16. Геометрический расчет зубчатой передачи
При построении картины зацепления межосевое расстояние О1О2 определяется по формуле (5.2). Диаметры начальных окружностей можно найти, рассмотрев треугольники О1АР и О2ВР ( рис. 5.15):
dW1 = mz1 (cos20˚ / cos αW); (5.6)
dW2 = mz2 (cos 20˚ / cos αW).
В таком случае начальное межосевое расстояние рассчитывается по формуле
aW = 0.5 m (z1 + z2) (cos20˚ / cos αW). (5.7)
Как уже указывалось, при работе зубчатой передачи начальные окружности перекатываются друг по другу без скольжения. В случае беззазорного зацепления толщина зуба на начальной окружности одного колеса равна ширине впадины на начальной окружности другого колеса
sW1 = eW2.
Выполнив подстановку соответствующих выражений для толщины зуба и ширины впадины и произведя соответствующие преобразования, получим:
inv αW = 2 tg20˚ (x1 + x2) / (z1 + z2) + inv20˚. (5.8)
Полученное выражение называется уравнением зацепления, оно позволяет определить угол зацепления, исходя из заданных чисел зубьев и коэффициентов смещений.
Формулы (5.6). (5.7), (5.8) образуют основу для геометрического расчета зубчатой передачи. В зависимости от сочетания коэффициентов смещений различают четыре варианта передач, представленных в таблице 5.1
Табл. 5.1. Варианты зубчатых передач
| x1 = x2 = 0 | ∑x = 0 | αW = 20˚ | dW = d | aW = a | нулевая передача | |
| x1 = - x2 | ∑x = 0 | αW = 20˚ | dW = d | aW = a | равносмещенная передача | |
| x1 ≠ 0, x2 ≠ 0 | ∑x > 0 | αW > 20˚ | dW > d | aW > a | положительная передача | |
| x1 ≠ 0, x2 ≠ 0 | ∑x < 0 | αW < 20˚ | dW < d | aW < a | отрицательная передача |
Иногда формулу (5.6) представляют в виде:
аW = a + y m,
где y - коэффициент воспринимаемого смещения:
y = 0.5 (z1 + x2) (cos 20˚ - cos αW) / cos αW.
Кроме того, вводится обозначение
∆ y = ∑ x – y,
где ∆y - коэффициент уравнительного смещения.
Согласно ГОСТ 16132- 72 расчет геометрических параметров зубчатой перeдачи следует вести с использованием этих коэффициентов.
5.17. Блокирующие контуры
Как уже было показано, коэффициенты смещения существенно влияют на качественные показатели зубчатой передачи и ее геометрию. Использование колес со смещением позволяет вписаться в заданное межосевое расстояние. При увеличении x растет контактная и изгибная прочность. Смещение влияет на скорость скольжения профилей, а значит на их износ. Помимо благоприятного влияния увеличение смещения ведет к заострению, интерференции, к снижению коэффициента перекрытия. Невозможно назначить смещение, оптимальное со всех точек зрения. Для каждой отдельной передачи следует рассмотреть всю совокупность эффектов, вызываемых смещением, что представляет весьма трудоемкую задачу.
С целью облегчения практического использования колес со смещением разработан метод блокирующих контуров. Результаты расчетов представлены в виде диаграмм, так называемых блокирующих контуров. Они позволяют обоснованно назначать коэффициенты смещения, не прибегая к трудоемким расчетам.

Рис. 5.17. К расчету толщины зуба
на окружности произвольного радиуса
Блокирующий контур строится для каждой пары чисел зубьев z1 и z2. На координатных осях откладываются значения x1 и x2 так, что точка А соответствует передаче, составленной из колес с положительным смещением, точка В – с отрицательным смещением, точка 0 - для нулевых колес (рис. 5.17). Таким образом, каждой точке координатного поля соответствует вариант передачи.
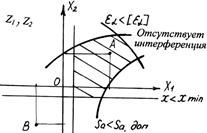
Рис. 5.18. Блокирующие контуры
Однако не все точки этого поля можно использовать. Некоторые неприемлемы по условию существования передачи: интерференции, подрезания, заострения, малого коэффициента перекрытия. Предельно допустимому значению каждого этого параметра соответствуют безусловные границы, эти границы в виде линий в совокупности образуют блокирующий контур. Для каждой пары чисел зубьев формы контура будут разными. Внутри контура могут быть нанесены условные границы, например, εα = 1.2, sa = 0.25 m, x = xmin и т. д. Блокирующие контуры для различных сочетаний чисел зубьев колес содержаться в соответствующих справочниках.
Косозубые колеса
Винтовые колеса с постоянным шагом винтовой линии называются косозубыми. Боковая поверхность зуба образуется чертящей прямой АВ, лежащей в производящей плоскости Р при обкатывании ее вокруг основного цилиндра Q. Если чертящая прямая параллельна образующей основного цилиндра, получается прямозубое колесо, если она составляет с образующей угол βb – косозубое. Каждая точка прямой описывает эвольвенту. Косозубое колесо можно рассматривать как множество прямозубых колес бесконечно малой толщины, сдвинутых друг относительно друга. Боковая поверхность зуба пересекает основной цилиндр по винтовой линии с углом подъема 90˚ - βb Угол подъема винтовой линии, измеренный на поверхности делительного цилиндра, находится на основании зависимости tg β = (r/rb) tg βb.
ассмотрим развертку делительного цилиндра на плоскости + рис.(5.18).На ней можно указать три шага зубьев: нормальный pn, торцевой pt, осевой pa. Соответственно этому имеется три модуля: нормальный mn, торцевой mt, осевой ma. Из построения на рис. следует, что Pt = pn cos β, следовательно mt = mn cos β.

Рис. 5.19. Косозубое колесо и его развертка на плоскость
Косозубые колеса изготавливаются тем же инструментом, что и прямозубые. Заготовка разворачивается относительно инструмента на угол β. В нормальном сечении зуб получается таким же, как у соответствующего прямозубого колеса. Размеры зубьев в торцевом сечении рассчитываются по приведенным выше формулам, но модуль принимается торцевой, выраженный через стандартный модуль инструмента.
Основная особенность косозубых колес состоит в том, что зубья входят в зацепление не по всей длине зуба, как это происходит в прямозубых колесах, а по контактной линии, параллельной образующей основного цилиндра, длина которой непрерывно изменяется. Благодаря этому увеличивается продолжительность контакта пары зубьев, что находит выражение в увеличении коэффициента перекрытия. Для косозубых колес коэффициент перекрытия
εγ = εα+ εβ,
где εα – коэффициент перекрытия соответствующего прямозубого колеса,
εβ - добавочный коэффициент перекрытия из-за наклона линии зуба:
εβ = φβ / τ,
где τ - угловой шаг.
Из построения на рис. 5.19 следует:
φβ = b tg β / r.
Достоинство косозубых колес – плавность работы, бесшумность, недостаток наличие осевого усилия на подшипники. Для устранения этого усилия применяют шевронные колеса, составленные из двух зубчатых колес с равным но противоположным наклоном зубьев..
Не нашли, что искали? Воспользуйтесь поиском: