Вычисление площадей плоских фигур

По первому свойству двойного интеграла , где S – площадь области D, 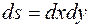, 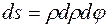. Следовательно, формулы для вычисления площади фигуры имеют вид:

в декартовой системе координат

; (8)

в полярной системе координат

. (9)

Задача 6.31 [10]

Найти площадь фигуры, ограниченной данными линиями:

, .

Литература: [5, гл. 8, § 1], [6, т. 2, гл. 1, § 3], [3, гл. 7, § 3], [9,
гл. 10, § 3].

Решение:

Построим фигуру (рис. 9).

Так как , то – область D для двойного интеграла. Найдем площадь фигуры по формуле (8).

Рис. 9

Окружность пересекается с параболой в точках 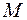и , координаты которых найдем, решая систему уравнений:

, , .

, тогда . , .

Двойной интеграл (8) лучше вычислять по второму правилу, т.е. по формуле (5). В этом случае не потребуется разбиения области на части. В то же время первое правило требует разбиения фигуры на две части прямой, проходящей через точки M и N, и тогда интеграл (8) представится суммой двух интегралов.

Неравенства (4) принимают вид:

, .

Действительно, прямые , ограничивают область D снизу и сверху. Слева область ограничена кривой (дуга 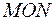параболы), справа – кривой (дуга окружности в правой полуплоскости).

Поэтому будет один двойной интеграл:

Вычислим первый интеграл отдельно:

Второй интеграл:

,

тогда .

Задача 7.31 [10]

Найти площадь фигуры, ограниченной данными линиями: , , , .

Решение:

Преобразуем первое и второе уравнения в декартовой системе координат, получим: , . Это окружности: первая – с центром в точке (0, 2), ; вторая – с центром в точке (0, 4), .

Построим фигуру (рис. 10): , .

Рис. 10

Область – фигура – является правильной в полярной системе координат. Найдем уравнения границ входа и выхода в полярных координатах.

Полагая в уравнении , , 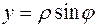получим:

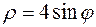, т.е. – полярное уравнение линии .

Аналогично для второй окружности:

, т.е. – полярное уравнение линии .

Неравенства (6) принимают вид:

, .

По формуле (9) площадь :

Не нашли, что искали? Воспользуйтесь поиском: