Преобразование Фурье – Бесселя

Это преобразование применимо к сигналам, обладающим круговой симметрией. Такие функции записываются в виде

f (x, y) = f () = f (r).

При этом вводимые ниже функция импульсного отклика h (x, y) и передаточная функция H (u, v) оптической системы имеют вид

h (x, y) = h () = h (r);

H (u, v) = H () = H (r).

Такие оптические системы должны содержать только такие элементы, двумерная функция пропускания которых сводится к функции, зависящей от одной переменной. К таким элементам относятся круговые диафрагмы, круглые линзы, зонные пластинки Френеля и т.д. Можно показать, что образы двумерных распределений, являющихся функциями только полярного радиуса r = , имеют также круговую симметрию (и, следовательно, представляют собой функции только радиальной пространственной частоты r = ). Преобразование Фурье – Бесселя имеет вид

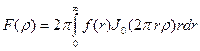, (8.2)

где J ₀ – функция Бесселя первого рода нулевого порядка. Соответствующее обратное преобразование записывается в виде

.

Видим, что преобразование Фурье – Бесселя является одномерным интегральным преобразованием с одинаковыми ядрами прямого и обратного преобразований (2 p ). Преобразование Фурье – Бесселя, называемое также преобразованием Ганкеля нулевого порядка, получается из двумерного преобразования Фурье при переходе в нем к полярной системе координат, как в координатной, так и в частотной области:

x = r cos q, y = r sin q, u = r cos j, v = r sin j, dxdy = rdrdq.

Подставив эти соотношения в преобразование Фурье, получим

F (r) =

= =

= .

Учитывая определение функции Бесселя первого рода нулевого порядка

,

придем к выражению (8.2).

С преобразованием Ганкеля мы уже встречались при рассмотрении дифракции Фраунгофера на круглом отверстии (интеграл (6.?)), апертурная функция t (x, y) которого обладает круговой симметрией:

t (x, y) = t (r) = t () =

где R – радиус отверстия.

1.3.3. Преобразование свертки

Понятие свертки имеет большое значение в оптике. Рассмотрим это понятие сначала на примере функций одной переменной. Сверткой s (x) двух функций f (x) и g (x) называют интеграл вида

s (x) = , (8.3)

где является вспомогательной переменной интегрирования. Кратко свертку записывают в виде или просто s (x) = Как видим, эта операция предполагает умножение ординаты функции f (x) при каждом значении целиком на другую функцию g (x), но смещенную по оси x > 0 на отрезок т.е. умножение на функцию и суммирование результатов, полученных при всех возможных значениях . Функция g (x) должна быть инвариантной относительно сдвига. Это означает, что. форма кривой g (x) не должна изменяться при смещении ее вдоль оси X на любое значение x = , так что кривые g (x) и g (x – ) должны иметь одинаковый вид при любом значении (функции g (x) и g (x – ) должны иметь одинаковую зависимость от x). Поскольку функция g (x) отлична от нуля только на ограниченном промежутке (a, b), то интегрирование в (8.3) по бесконечным пределам следует заменить на интегрирование в пределах (a, b).

Аналогично определяется свертка функций двух переменных:

s (x, y) = 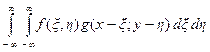. (8.4)

Этот интеграл называют двумерной сверткой. Обратного преобразования свертка не имеет

Смысл одномерного интеграла свертки заключается в следующем. Для нахождения интеграла (8.3) следует построить зеркальное отражение функции относительно оси ординат. Полученную функцию сдвинуть вдоль оси абсцисс вправо на отрезок x, произвести поточечное умножение сдвинутой функции g (x – ) на f () и вычислить площадь под кривой f () g (x – ). В результате мы получим значение функции s (x) в одной конкретной точке x. Повторяя указанные действия для различных значений сдвига x, можно построить функцию s (x) в соответствии с формулой (8.3).. Интегрирование в интеграле (8.3) распространено на бесконечные пределы, так как только относительно близкие к точке x точки будут оказывать влияние на величину s (x), ибо кривая g (x) довольно узкая.

Рассмотрим физическую сторону операции свертки (рис. 8.2). Ордината f (x) кривой f (x) при некотором значении x ₁ (рис.8.2, а) после умножения на функцию g (x – x ₁) (рис. 8.2, б) размывается, становясь кривой 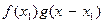(сплошная кривая на рис. 8.2, в). Ордината этой кривой при x = x ₁ дает основной вклад в значение функции s (x) в точке x ₁.

Рис. 8.2

Имеются и другие вклады, которые порождаются размытием других ординат кривой f (x). Один из таких вкладов, возникающих из-за размытия ординаты кривой при x = и равный ординате кривой f () g (x – ) в точке x ₁, т.е. величина f () g (x ₁ – ), представлена на рис. 8.2, в пунктирным вертикальным отрезком. Результирующее значение функции s (x) в точке x ₁ будет определяться суммой указанных вкладов, т.е. интегралом (8.3).

Из проведенного рассмотрения видно, что свертку можно трактовать как суммарное влияние распределения одной функции в соответствии с законом, определяемым другой функцией. Это влияние и приводит к изменению вида функции f (x) и к искажению сигнала (например, к размытию изображения), описываемого этой функцией.

В теории линейных систем, в том числе и в оптике, широкое применение находит так называемая теорема свертки, согласно которой фурье-преобразование свертки двух функций равно произведению их собственных фурье-преобразований, т.е.

F{ s (x)} = F{ f (x)* g (x)} = F{ f (x)}×F{ g (x)}

- в одномерном случае и

F{ s (x, y)} = F{ f (x, y)* g (x, y)} = F{ f (x, y)}×F{ g (x, y)}

– в двумерном случае. Докажем эту теорему для одномерного случая. Запишем, используя определение преобразования Фурье:

F{ s (x)} = .

Заменяя s (x) сверткой функций f (x) и g (x) и изменяя затем порядок интегрирования, получим

F{ s (x)} = =

= .

Во внутреннем интеграле, в котором x является постоянной величиной, произведем замену переменной x – x = h. Будем иметь

F{ s (x)} = .

Множитель exp(– i 2 pux) является постоянным в пределах внутреннего интеграла, и поскольку остальная часть подынтегрального выражения внутреннего интеграла не содержит переменную x, она является постоянной для внешнего интегрирования по отношению к x. Таким образом, полное выражение разделяется на произведение двух отдельных интегралов:

F{ s (x)} = =

= F{ f (x)}×F{ g (x)}.

Теорема свертки доказана.

Из теоремы свертки вытекает, что свертке в обычном (физическом) пространстве соответствует умножение в фурье-пространстве (в пространстве частот u, v). Этот очень важный вывод позволяет не только наглядно объяснить процесс формирования оптического изображения, но и служит для получения так называемых передаточных функций системы.

Справедлива и обратная теорема (называемая второй теоремой свертки, или теоремой Парсеваля): фурье-преобразование произведения двух функций равно свертке фурье-образов этих функций, т.е.

F{ f (x, y)× g (x, y)} = F{ f (x, y)}*F{g(x, y)}.

Свертка обладает свойством коммутативности:

s (x, y) = =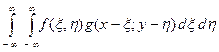

= ,

или в символическом виде:

f (x, y)* g (x, y) = g (x, y)* f (x, y);

в одномерном случае:

s (x) = = ,

или

f (x)* g (x) = g (x)* f (x).

Операция свертки широко используется при описании кратных процессов дифракции или последовательного наложения нескольких взаимно подобных процессов; связывает сигналы на входе и выходе оптической системы. Линейные оптические системы по своей природе обладают двумя степенями свободы. Поэтому они могут осуществлять преобразование двух типов: преобразование

s (x, h) =

и преобразование (8.4). Наибольшее значение свертка имеет в теории формирования и обработки оптического изображения. Одной из сворачиваемых функций 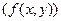здесь является распределение либо амплитуды, либо интенсивности поля на предмете, а второй (g (x, y)) – либо импульсная функция, либо сглаживающая функция (называемая часто размытием), функция рассеяния (изображения) линии (ФРЛ, в одномерном случае) или функция рассеяния точки (ФРТ). Функция s (x, y) в этом случае представляет собой распределение либо амплитуды, либо интенсивности поля на изображении. Термины «функция рассеяния», «размытие» отражают тот факт, что операция свертки, производимая оптической системой, приводит к размытию, нерезкости изображения.

Возможно образование свертки и более чем двух функций,

которая также имеет физический смысл, в частности, в оптике (в интерферометрии, спектроскопии, голографии и т.д.).

Покажем, что апертурную функцию щелевой решетки можно

Рис. 8.3

представить сверткой апертурной функции одиночной щели и последовательности d -функций определяющей структуру решетки. В основе такого представления лежит сформулированная выше теорема свертки. Поскольку, как было показано в п. 7.7.5, распределение амплитуды светового поля в дифракционной картине решетки является преобразованием Фурье от ее апертурной функции t (x), а, с другой стороны, это

распределение представляет собой произведение фурье – преобразований апертурной функции t ₁(x) одиночной щели и последовательности d -функций, определяющей структуру решетки, то на основании теоремы свертки приходим к сформулированному выше утверждению о том, что апертурная функция решетки t (x) может быть описана как свертка апертурной функции t ₁(x) одиночной щели с последовательностью d -функций, определяющей распределение этой щели в решетке, т.е. с функцией f (x). На основании свойства коммутативности свертки функцию t (x) можно представить и как свертку функции f (x) с функцией t ₁(x):

t (x) =

Образование такой свертки показано на рис. 8.3. Обратим внимание на следующий факт. В примере на рис. 8.1 при образовании свертки происходит перекрытие ординат сворачиваемых функций; в случае же с решеткой такое перекрытие отсутствует.

Корреляция

Корреляция является широко распространенным методом обработки различных сигналов. Она находит применение и в оптике. С понятием корреляции мы уже встречались в третьей главе. Корреляция является, по существу, методом оценки и определения взаимных связей, имеющих форму подобий или совпадений. Пусть имеем одном6ерный зависящий от времени детерминированный сигнал f (t) конечной длительности. Интеграл

где τ – величина временного сдвига сигнала, называется автокорреляционной функцией сигнала f (t). Она характеризует степень связи (корреляции) сигнала f (t) со своей копией, сдвинутой на величину τ по оси времени. Так как любой сигнал

полностью коррелирован с самим собой, то ясно, что при τ = 0 корреляционная функция достигает максимума. При этом величина определяет энергию сигнала. Как видим, максимальное значение автокорреляционной функции равно энергии сигнала.

С увеличением τ корреляционная функция убывает и при сдвиге τ, превышающем длительность сигнала, автокорреляционная функция обращается в нуль.

Заменив время t на пространственную переменную x, получим автокорреляционную функцию одномерного пространственного сигнала f (x):

с (a) =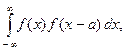

где a – величина сдвига сигнала f (x) вдоль положительного

направления оси X. Сигнал f (x) имеет отличные от нуля значения только в конечном интервале значений переменной x. Функция c (a) имеет максимум при a = 0 и обращается в нуль при тех значениях а, при которых функции f (x) и f (x - а) перестают перекрываться.

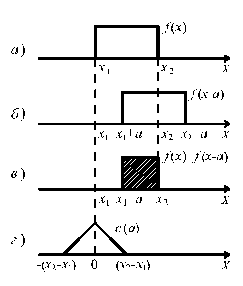
На рис.8.4. показано построение автокорреляционной функции для простейшего сигнала в виде прямоугольного импульса, координаты начала и конца которого равны соответственно x ₁ и x ₂ (рис. 8.4, а). Сдвинутый на величину а по оси x > > 0 сигнал f (x – a) показан на рис. 8.4, б, а произведение – на рис. 8.4, в в виде площади заштрихованного прямоугольника. График функции с (a) представлен на рис. 8.4, г. Каждому значению а соответствует свое произведение и своя площадь под его графиком. Численные значения таких площадей для соответствующих значений а и дают ординаты функции с (a). Таким образом, значение с (a) для любых выбранных значений а получается смещением функции относительно себя самой на величину а и определением площади перекрытия.

Для оценки степени связи между двумя различными сигналами

f (x) и g (x) используется взаимная корреляционная (или кросскорреляционная) функция, определяемая как

Рис. 8.4

с ₁₂ (а) =

Автокорреляционная функция с (a) является частным случаем функции с ₁₂ (a), когда сигналы f (x) и g (x) одинаковы.

Чтобы кросскорреляционную функцию можно было описать сдвигом а и в отрицательном направлении оси X следует ее переписать следующим образом:

с ₁₂ (а) =

и аналогично для автокорреляции.

Обе корреляционные функции могут быть определены и для двумерных сигналов. В частности, кросскорреляционная функция двумерных сигналов f (x, y) и g (x, y)

c ₁₂ (a, b) = =

=

Здесь a и b – смещения функции g (x, y) вдоль координатных осей X и Y соответственно.

Для обозначения корреляции будем использовать символ ◦ Тогда c (a, b) = f (x, y) ◦ f (x, y) и c ₁₂ (a, b) = f (x, y) ◦ g (x, y).

Определение функции одномерной взаимной корреляции часто выражается в несколько иной форме, а именно:

с ₁₂ (x) = f (x) ◦ g (x) =

и аналогично для автокорреляции. В этом выражении x является смещением, а x – вспомогательной переменной интегрирования.

Отсюда видно, что корреляция подобна свертке, но отличается тем, что функция g (x) сдвигается, а не переворачивается (перегибается). В двумерном случае:

c ₁₂ (a, b) = f (x, y) ◦ g (x, y) =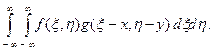

Если функции f (x) и g (x) комплексные, то принято определять комплексную автокорреляционную функцию

с (x) = f (x) ◦ =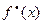

и комплексную кросскорреляционную функцию

с ₁₂ (x) = f (x) ◦ g (x) =

При этом, если звездочка связана с другой функцией, то получается сопряженный результат. Отметим также, что

f (x) ◦ g (x) = f (x) g (- x)

Часто бывает удобно нормировать корреляцию. Для этого корреляционные функции делят на центральное значение корреляции, т.е. на значение при x = 0 (нулевой сдвиг). В итоге получаем нормированную автокорреляционную функцию

и нормированную кросскорреляционную функцию

.

.

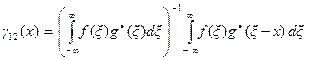
1.3.5. Преобразование Френеля

Значение преобразования Френеля в оптике тесным образом связано с явлением дифракции Френеля. Примером преобразования Френеля является зонная пластинка Френеля.

В своем основном виде двумерное преобразование Френеля определяется следующим образом

Ф (x, y) =

= (8.5)

где f (x, y) – исходная функция, а Ф (x, y) – ее френелевский образ. Мы видим, что двумерное преобразование Френеля представляет собой просто двумерную свертку функции f (x, y) с экспоненциальной фазовой функцией

Z (x, y) = exp [ ip s (x ² + y ²) / l ],

представляющей собой двумерную функцию Гаусса с мнимым комплексно сопряженным аргументом и называемой функцией Френеля. Интегральное преобразование Френеля какой-либо функции можно рассматривать и как свертку этой функции с зонной пластинкой Френеля. Каждая точка области задания функции размывается при этом в картину зон Френеля. Можно считать, что при преобразовании Френеля исходная функция представляет собой сумму большого числа последовательно смещенных френелевских картин. Величина каждой составляющей картины находится посредством умножения функции на соответствующую френелевскую картину и интегрирования. Таким образом, при преобразовании Френеля каждое значение функции f (x, y) в точке (x, y) размывается функцией Френеля, а затем все непрерывно смещенные картины Френеля суммируются.

Френелевский образ функции f (x, y) можно найти и по формуле

Ф (x, y) = f (x, y)* Z (x, y) = ,

где F (u, v) – фурье-образ функции f (x, y), Z (u, v) – фурье-образ функции Френеля:

Z (u, v) = =

.

При получении этого результата была использована формула (6.21) для , , . Как видим, фурье-образ функции Френеля в координатах пространственных частот u, v равен функции Френеля в координатах x, y, умноженной на комплексный коэффициент . Аналогичным свойством обладает лишь двумерная функция Гаусса фурье-образ которой равен самой функции Гаусса.

Преобразование Френеля, как и преобразование Фурье, дает однозначное представление функции, являясь операцией, допускающей восстановление исходной функции при повторном, или обратном преобразовании Френеля. Обратное преобразование также имеет вид свертки

f (x, y) =

= .

В обратном преобразовании аргумент фазовой функции Френеля заменяется на комплексно сопряженный. Заметим, что при преобразовании Френеля, которое является сверткой, все операции производятся в обычном координатном пространстве. Этим оно качественно отличается от преобразования Фурье, в результате которого преобразуемая функция превращается в ее частотно-спектральный образ, заданный в пространстве фурье-координат, или пространственных частот. В преобразовании Френеля параметр s в большинстве случаев интерпретируется как кривизна сферических волновых фронтов.

Сравнивая интеграл суперпозиции в приближении Френеля (6.19), записанный в виде

,

с выражением (8.5), видим, что этот интеграл представляет собой двумерное преобразование Френеля с ядром преобразования

h (x,y) = ,

являющимся, как мы увидим ниже, импульсным откликом слоя свободного пространства в приближении Френеля. Кривизна сферического волнового фронта 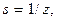где z – толщина слоя свободного пространства.

Таким образом, можно констатировать, что поле в ближней зоне при дифракции плоских волн можно определить с помощью двумерного преобразования Френеля. Если амплитуда Е ₀ падающей волны в плоскости апертуры постоянна, то в силу соотношения поле в плоскости X¢Y¢, расположенной в ближней зоне, можно определить с помощью преобразования Френеля от апертурной функции 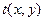. Видим также, что в приближении Френеля интеграл суперпозиции представляет собой свертку функции распределения комплексной амплитуды поля в плоскости непосредственно за апертурой с импульсной характеристикой свободного пространства в приближении Френеля.

По известному распределению E (x¢, y ¢) с помощью обратного преобразования Френеля

E (x, y) =

=

можно восстановить распределение поля в плоскости непосредственно за апертурой.

Между преобразованиями Френеля и Фурье существует тесная связь, обусловленная тем, что первое преобразование воспроизводит дифракцию Френеля, а второе – дифракцию Фраунгофера. Различие между обоими преобразованиями зависит только от расстояния, при котором проявляются оба типа дифракции. Связь между этими преобразованиями проще всего установить в одномерном случае. Воспользовавшись преобразованием Фурье, будем иметь:

F (x) = =

.

Отсюда видно, что фурье-образ F (x) функции f (x) получается путем умножения функции f (x) на функцию exp(-ipx ²), применения к полученному результату преобразования Френеля и последующего умножения на функцию . Это соотношение позволяет представить преобразование Фурье с помощью операций умножения и свертки. При этом каждое из этих действий может быть осуществлено с помощью соответствующей оптической системы.

Преобразование Френеля играет важную роль не только при описании дифракции Френеля, но и при описании свободного распространения когерентных оптических полей. Оно используется в оптике так же часто, как и преобразование Фурье. Использование обоих интегральных преобразований обусловлено тем, что пространство изменяет распространяющиеся в нем световые волны согласно этим преобразованиям. Распространение света между элементами оптической системы (например, между линзами в оптической системе формирования изображения) также можно описать с помощью преобразования Френеля (или свертки с фазовым множителем, являющимся импульсной характеристикой слоя свободного пространства). Преобразование Френеля применяется и при исследовании голограмм Френеля и анализе систем воспроизведения с апертурами, кодированными зонной пластинкой.

1.3.6. Преобразование Абеля

Как и преобразование Фурье – Бесселя, преобразование Абеля применимо к оптическим системам, обладающим вращательной симметрией. Это преобразование связывает функцию одной переменной x (или y) с функцией одной переменной r = = и имеет вид

g (x) = 2 .

Обратное преобразование Абеля определяется соотношением

f (r) . (8.6)

Прямое и обратное преобразования Абеля по существу являются частным решением общей задачи восстановления многомерного объекта по известным проекциям.

Изменением переменной преобразование Абеля можно свести к интегралу свертки. В этом виде преобразование Абеля называется модифицированным. Вследствие своей пространственной инвариантности такое преобразование позволяет при анализе использовать методы Фурье и удобно для вычислительных целей. Можно показать, что преобразования Абеля, Фурье – Бесселя и Фурье тесно связаны. Последовательное применение этих преобразований к некоторой функции дает исходную функцию. В оптике этот факт выражается в соотношениях между вводимой ниже функцией рассеяния точки и функцией рассеяния линии (преобразование Абеля), между линейной функцией рассеяния и (одномерной) передаточной функцией (преобразование Фурье) и между вводимой ниже оптической передаточной функцией и функцией рассеяния точки (преобразование Фурье – Бесселя).

Не нашли, что искали? Воспользуйтесь поиском: