Устойчивость систем по части переменных. Основные определения и теоремы

Пусть дана приведенная по Ляпунову система (см. п. 1.3)

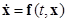(2.5.1)

с областью определения правых частей вида

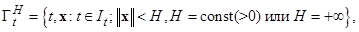(2.5.2)

причем функция удовлетворяет следующим свойствам в области (2.1.2):

а) f - непрерывна по t и x;

б) f - непрерывно дифференцируема по x и

(вследствие непрерывности по известной теореме

Вейерштрасса)все частные производные ,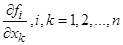

ограничены на любом компактном подмножестве (2.5.3)

из области (2.1.2);

в) , т.е. система (2.5.1) допускает

тривиальное решение

Будем рассматривать часть переменных вектора состояния системы .

Сначала (в определениях 1, 2) допустим, что условие (2.5.3,в) отсутствует.

Определение 1. Фиксированное решение системы (2.5.1)÷(2.5.3) называется устойчивым по Ляпунову относительно части переменных 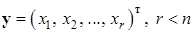, если и такое, что для всех решений , удовлетворяющих неравенству

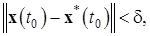
выполняются следующие требования:

(а) все решения , включая фиксированное решение — бесконечно продолжимы вправо;

(б) выполняется неравенство:

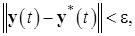где

■

Определение 2. Фиксированное решение системы (2.5.1)÷(2.5.3) называется асимптотически устойчивыми по части переменных , если:

(а) оно устойчиво по этой части переменных у (в смысле определения 1);

(б) существует некоторое положительное число такое, что для всех решений , удовлетворяющих неравенству для части переменных выполняется предельное соотношение:

,

где 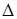– окрестность называется областью притяжения решения по части переменных y. ■

Определение 3. Функция Ляпунова (для системы (2.5.1)÷(2.5.3)) (здесь и далее уже полагаем, что система (2.5.1)÷(2.5.3) допускает тривиальное решение) называется положительной определенной функцией Ляпунова по части переменных y, если:

(а) она является знакопостоянной положительной по всем переменным x, т. е. (в некоторой области );

(б) существует положительная определенная не зависящая от времени функция Ляпунова по части переменных y, такая, что

■

Определение 4. Говорят, что функция Ляпунова вида , положительно определенная по части переменных, допускает БМВП при по части переменных y, если существует не зависящая от времени функция Ляпунова по части переменных, положительно определенная и такая что:

(сильный БМВП).■

В 1970-72 гг. В. В. Румянцев доказал две модификации первой и второй теорем Ляпунова об устойчивости и асимптотической устойчивости по части переменных.

Теорема об устойчивости по части переменных. (В. В. Румянцев, 1970-72 г.г.)

Тривиальное решение системы (2.5.1)÷(2.5.3) является устойчивым по части переменных , , если найдется (существует) функция Ляпунова , обладающая следующими свойствами:

1) – положительно определенная по части переменных у (в смысле определения 3);

2) является знакопостоянной отрицательной функцией Ляпунова (по всем переменным х).■

Доказывается аналогично доказательству первой теоремы Ляпунова (об устойчивости) (без доказательства).

Теорема об асимптотической устойчивости по части переменных. (В. В. Румянцев, 1970-72 г.г.)

Тривиальное решение системы (2.5.1)÷(2.5.3) является асимптотически устойчивым по части переменных у, если существует функции Ляпунова , обладающая следующими свойствами:

1) – положительно определенная по части переменных у (в смысле определения 3);

2) – допускает БМВП по части переменных (в смысле определения 4), т.е. сильный БМВП;

3) , где – положительно определенная не зависящая от времени функция Ляпунова по части переменных у. □

Сравнить со второй теоремой Ляпунова (об асимптотической устойчивости) (без доказательства).

Замечания.

1. Можно сформулировать определение экспоненциальной устойчивости фиксированного решения нелинейной нестационарной системы (5.1.1)÷(5.1.3) (не обязательно допускающей тривиальное решение по всем переменным х) по части переменных , опираясь, как на аналоги, на данные выше определения экспоненциальной устойчивости (по всем переменным 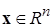) и асимптотической устойчивости по части переменных 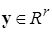(В. В. Румянцев) (самостоятельно).■

2. Можно сформулировать соответствующую теорему, аналогичную теореме Н. Н. Красовского (1959 г.) о необходимых и достаточных условиях существования функции Ляпунова, удовлетворяющей оценкам, характерным для квадратичных форм, (по аналогии с теоремами В. В. Румянцева об устойчивости и асимптотической устойчивости фиксированного решения по части переменных (самостоятельно). ■

3. Можно сформулировать аналогичные определения и теоремы о диссипативности систем по части переменных (самостоятельно). ■

[1] Областью в функциональном анализе называется открытое связанное множество

Не нашли, что искали? Воспользуйтесь поиском: