Вычислимые, частично рекурсивные и общерекурсивные функции

Пусть функция у зависит от целочисленных аргументов х₁,х₂,...х_п.

Функция у = f (x₁, x₂, …, x_n) называется эффективно вычислимой, если суще­ствует алгоритм, позволяющий вычислять ее значения. Простейшие эффек­тивно вычислимые функции:

1. λ(x) = x + l — оператор сдвига.

2. 0(х) = 0 — оператор аннулирования.

3. 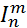(х₁,х_2,...,х_п) = х_т, 1 <т<п —оператор проектирования.

Рассмотрим функции f₁(x₁, x₂, …,x_n), f₂ (x₁, x₂, …, x_n),…, f_m(x₁, x₂,…, x_n) и функцию φ (x₁, x₂, …, x_n), а функцию ψ(x₁ ,х₂,...,х_п) определим равенством

ψ (x₁ ,х₂,...,х_п) = φ (f₁(x₁, x₂, …,x_n), f₂ (x₁, x₂, …, x_n),…, f_m(x₁, x₂,…, x_n)).

Ясно, что функция ψ(x₁ ,х₂,...,х_п) получена суперпозицией функций φ(x₁, x₂, …, x_n) и f₁(x₁, x₂, …,x_n), f₂ (x₁, x₂, …, x_n),…, f_m(x₁, x₂,…, x_n ). Очевидно, что если все функции f₁, f₂,…,f_m и φ всюду определены, то ψ всю­ду определена. Функция у будет не всюду определена, если хотя бы одна из функций f₁, f₂,…,f_m не всюду определена или если f₁, f₂,…,f_m всюду оп­ределены, но φ (f₁, f₂,…, f_m) где-то не определена и т. п.

Формулы примитивной ре­курсии символически изображают так:

f = R(φ, ψ) и рассматривают R как символ двухместной операции, определенной на множестве F функций.

Функция f называется просто примитивно рекурсивной, если ее можно по­лучить конечным числом операций подстановки и примитивной рекурсии исходя лишь из простейших функций λ, O, 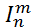. Операции подстановки (су­перпозиции) и примитивной рекурсии, будучи применены ко всюду опреде­ленным функциям, дают в результате снова всюду определенные функции. Поэтому все примитивно рекурсивные функции всюду определены.

Функция f(х₁, х₂,,.,,х _n) называется частично рекурсивной, если она может быть получена за конечное число шагов из простейших функций λ, O, 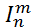при помощи операции суперпозиции, схем примитивной рекурсии и операции минимизации.

Функция называется общерекурсивной, если она частично рекурсивна и всюду определена.

Тезис Черча: каждая интуитивно вычислимая функция является частично рекурсивной.

1. Найти функцию f(x, y), полученную из функции g(x)и h(x, y, z) по схеме примитивной рекурсии.

g(x) = x², h(x, y,z)= xz

2. Найти функцию f(x, y), полученную из функции g(x)и h(x, y, z) по схеме примитивной рекурсии.

g(x) = 0, h(x, y, z)= x + y + z

3. Доказать, что следующие функции примитивно рекурсивны:

a) f (x) = x + n

b) f (x) = n

c) f (x,y) = x + y

Машины Тьюринга

Тезис Черча нельзя доказать, т. к. он связывает нестрогое математическое понятие интуитивно вычислимой функции со строгим математическим поня­тием частично рекурсивной функции. Но в поддержку этого тезиса впослед­ствии другими авторами были приведены очень веские доводы.

В 1936 г. Тьюрингом был определен еще один класс интуитивно вычислимых функций и сформулирован тезис Тьюринга, эквивалентный тезису Черча. В результате попыток разложить интуитивно известные нам вычислительные процедуры на элементарные операции построена математическая модель, называемая машиной Тьюринга. Повторения элементарных операций, опре­деленных в этой машине, достаточно для проведения любого возможного вычисления. От человека-вычислителя эта машина отличается двумя осо­бенностями:

o она не ошибается, т. е. она без всяких отклонений выполняет правила, установленные для ее работы;

o она снабжена потенциально бесконечной памятью. Это значит, что хотя в каждый момент количество накопленной ею информации конечно, для этого нет никакой верхней грани. В качестве накопителя рассматривается бесконечная лента.

Машина Тьюринга включает:

1. Внешний алфавит А = {a₀,a₁,…, a_m} т. е. конечное множество символов. В этом алфавите (в символах этого алфавита) информация вводится в ма­шину. Машина перерабатывает введенную информацию в новую.

2. Внутренний алфавит

Q = .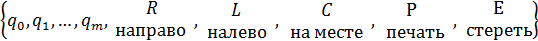

Иногда символы С,Р,Е отсутствуют. Символы 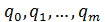выражают конечное число состояний машины, причем q₁ — начальное состояние, q_Q — стопсостояние.

3. Бесконечную в обе стороны ленту, представляющую память машины. Эта память разбита на клетки. В каждую клетку может быть записана только одна буква. а₀ — пустая клетка, она всегда может появиться при движе­нии вправо или влево, если закончится слово исходной информации

a₀a₁a₂...a _n.

4. Управляющую головку. Она передвигается вдоль ленты и может оста­навливаться напротив какой-либо клетки и воспринимать записанный там символ исходного слова. В одном такте работы машины управ­ляющая головка может сдвигаться только на одну клетку или оставать­ся на месте.

Работа машины складывается из тактов, по ходу которых происходит пре­образование начальной информации в промежуточную. В качестве началь­ной информации на ленту можно подать любую конечную систему знаков внешнего алфавита, расставленную произвольным образом по ячейкам. При этом работа машины Тьюринга может заканчиваться так:

после конечного числа тактов машина останавливается в q₀ состоянии. При этом на ленте оказывается переработанная информация. В этом слу­чае говорят, что машина применима к начальной информации I₁ и пере­рабатывает ее в результирующую информацию I₂;

машина никогда не останавливается (не переходит в q₀ состояние). В этом случае машина не применима к начальной информации I₁.

В таком такте работы машина Тьюринга действует по единой функциональной схеме.

Теорема. Все словарные функции, вычислимые по Тьюрингу, являются частично рекурсивными.

Тезис Тьюринга. Любая вычислимая функция вычислима по Тьюрингу.

Задание. Построить машину Тьюринга для правильного вычисления функции х + y.

Не нашли, что искали? Воспользуйтесь поиском: