Моделирование непрерывных случайных величин

Рассмотрим методы моделирования непрерывной случайной величины Х. Пусть f(x) – плотность распределения, а − функция распределения вероятностей случайной величины Х. Обозначим через F^-1(y) – функцию, обратную к F(x). Покажем, что распределение случайной величины

x=F^-1(ζ), (4.5)

где ζ – базовая случайная величина, имеет функцию распределения F(x). Действительно (рис. 4.2),

P(X<x)=P[ζ<F(x)]=F(x).

Следовательно, алгоритм моделирования непрерывной случайной величины сводится к определению значения этой величины по (4.5) через реализацию базового случайного числа.

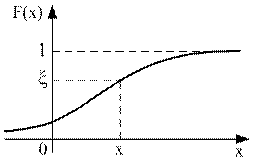
Рис. 4.2

В качестве примера рассмотрим экспоненциальное распределение с плотностью f(x)=λe^-λx, x≥0 и функцией распределения F(x)=1−e^-λx, x≥0. Находим обратную функцию распределения x=(−1/λ)lnζ, которая и определяет алгоритм моделирования.

Недостатком алгоритмов обратной функции является вычисление функции, обратной функции распределения. Большинство распределений не позволяет определить эту функцию в явном виде через элементарные функции. Поэтому трудоемкость алгоритмов определяется трудоемкостью решения относительно х уравнения вида

. (4.6)

Другой, широко используемый метод моделирования, состоит в представлении исходного распределения в виде смеси других, более простых с точки зрения имитации распределений:

f(x)=p₁f₁(x)+p₂f₂(x)+…+p_Sf_S(x), (4.7)

где p₁+p₂+…+p_s=1, f_i(x) – некоторые плотности распределения. Тогда имитация осуществляется в два этапа. Сначала имитируется выбор одного из S распределений, затем разыгрывается значение случайной величины с этим распределением. Первое базовое число используется для моделирования дискретной случайной величины с рядом распределения вероятностей (p₁,p₂,…,p_S), второе (или последующие) – для моделирования случайной величины с распределением f_i(x) (i=1,2,…,S) в зависимости от предшествующего результата.

Укажем ещё один способ моделирования случайных величин. Так, нормальное распределение, распределение Эрланга, χ² – распределение и ряд других могут быть представлены в виде суммы (композиции) более простых случайных величин.

В таблице 4.3 приведены алгоритмы имитации распределений, рассмотренных в разделе 2.

Как правило, при решении важных задач методом имитационного моделирования исследователь проверяет качество генерирования псевдослучайной последовательности.

Эта задача решается с использованием критериев согласия. Отличие применения этих критериев при оценке качества генерирования от классической задачи сглаживания статистических рядов заключается в том, что исследователь априори задаёт закон распределения и требуемые значения параметров псевдослучайной (сгенерированной) последовательности, а при решении задачи сглаживания необходимо решить задачу идентификации закона распределения.

При оценке качества генерирования псевдослучайной последовательности в качестве теоретического закона распределения возможно использование:

1. заданного закона распределения с заданными параметрами;

2. заданного закона распределения с уточненными параметрами путём решения задачи аппроксимации закона распределения тем или иным способом.

Рассмотрим последовательность этапов решения задачи оценки качества генерирования применительно ко второму случаю, как более общему (рис. 4.3).

Рис. 4.3 – Схема алгоритма оценки качества генерирования ПСП

После ввода исходных данных первым шагом в решении этой задачи является построение гистограммы наблюдаемого статистического ряда . Для этого необходимо выполнить следующие этапы:

1. Определить диапазон изменения статистического ряда x_min−x_max.

2. Определить ширину дифференциального коридора:

, (4.7)

где М – количество дифференциальных коридоров.

3.Определить частоту попадания анализируемой случайной величины в j-ый дифференциальный коридор:

, (4.8)

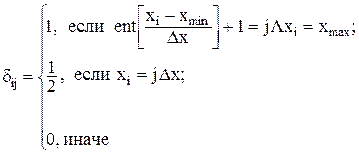где (4.9)

− индикатор состояния.

Следует отметить, что δ_i,j+1=1/2, если x_i=jΔx x≠x_max, т.е. в этом случае в j и j+1 коридоры добавляется по 1/2.

4. Если частота попадания в какой-либо k-ый дифференциальный коридор мала (p_j<0,01÷0,02), то для уменьшения влияния случайности его объединяют с k+1 коридором. Эта операция может быть применена неоднократно.

Исходным материалом для построения гистограммы является сгруппированный по дифференциальным коридорам статистический ряд, представленный, как правило, в виде таблицы (см. табл. 4.1), где

Статистический ряд

Табл. 4.1

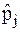
	0,099	0,1006	0,1003	0,0989	0,099	0,1067	0,0954
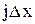
	0,1	0,2	0,3	0,4	0,5	0,6	0,7
	0,99	1,006	1,003	0,989	0,99	1,067	0,954
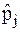
	0,1008	0,0997	0,0996
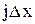
	0,8	0,9
	1,008	0,997	0,996

После построения гистограммы и оценки статистических характеристик решают задачу уточнения параметров распределения, используя тот или иной метод аппроксимации закона распределения.

Заключительным этапом решения задачи является проверка качества генерирования с использованием критериев согласия. Применение критериев согласия здесь полностью аналогично тому, как это делалось ранее. На основании данного статистического материала необходимо проверить гипотезу H, состоящую в том, что случайная величина Х подчиняется заданному закону распределения. Введем случайную величину U, являющуюся мерой расхождения теоретического и статистического распределений. Закон распределения этой случайной величины f_u(u) зависит как от закона распределения случайной величины X, так и от числа опытов N. Если гипотеза Н верна, то f_u(u) определяется законом распределения f_a(х) и числом опытов N.

Вычислим вероятность события Р(u ≤ U) = Р_д. Если эта вероятность мала, то гипотезу следует отвергнуть как малоправдоподобную, если значительна − экспериментальные данные не противоречат гипотезе Н. Далее в лабораторных работах будут использованы критерии Пирсона и Колмогорова – Смирнова.

Если уточнение параметров распределения сгенерированной последовательности не производится, т.е. не решается задача аппроксимации законов распределения, оценка качества генерирования ПСП производится с использованием в качестве теоретического распределения заданного закона с заданными параметрами. Для уточнения параметров распределения часто применяется метод моментов. Согласно этому методу, параметры распределения α₁,…,α_m выбираются таким образом, чтобы несколько важнейших числовых характеристик (моментов) теоретического распределения были равны статистическим характеристикам. При составлении уравнений для определения неизвестных параметров, как правило, выбирают моменты низших порядков. Общими рекомендациями являются здравый смысл и простота решения полученной системы уравнений. Рассмотрим несколько примеров.

Определим параметры аналитического выражения плотности распределения вероятностей генератора «белого шума» − стандартной программы ПЭВМ. Теоретически закон распределения должен быть равномерным с параметрами a=0, b=1.

Гистограмма приведена на рис. 4.4, а данные для расчётов − в таблице 4.1.

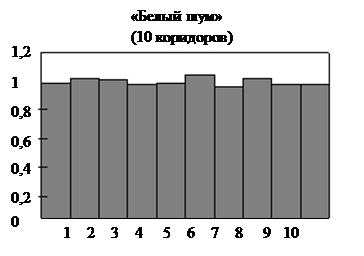Рис. 9.4

Уравнения для определения двух неизвестных параметров распределения могут быть составлены различными способами. Потребуем, например, чтобы у статистического и теоретического распределений совпадали математическое ожидание и дисперсия:

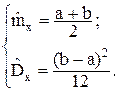(4.10)

Отметим, что оценка начальных моментов статистического ряда определяется выражением:

, (4.11)

где 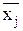- среднее значение j интервала, а центральных –

. (4.12)

Эта система уравнений имеет аналитическое решение:

(4.13)

Для данного статистического распределения

(4.14)

Подставив найденные оценки в выражения (4.13), получим: а=0,003327, b=0,996553. Отсюда видно, что рассчитанные параметры закона распределения незначительно, но отличаются от заданного при генерировании. Следовательно, при проведении статистического моделирования целесообразно проверять качество программных генераторов и оценивать его реальные характеристики.

Применив критерий Пирсона, вычислим значение

χ²= 7,77, что соответствует вероятности Р_д>0,3 (приложение табл. 4). Таким образом, можно принять гипотезу о том, что данный статистический ряд соответствует равномерному распределению с найденными параметрами.

Преимуществом метода моментов является простота определения параметров распределения, недостатком − неоднозначность в выборе уравнений, которых может быть большое количество.

Не нашли, что искали? Воспользуйтесь поиском: