Кинетическая энергия вращающего тела. Момент инерции

Рассмотрим вращательное движение твердого тела относительно неподвижной и проходящей через него оси. Разобьем это тело на множество элементарных объемов, масса каждого из которых равна Dm_i и радиус вращения r_i (Рис.3).

Рис.3.

Кинетическая энергия i – го элемента равна

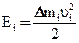(1)

Кинетические энергии различных элементов будут разными, т.к. различны их линейные скорости. Чтобы рассчитать полную энергию вращательного движения твердого тела, необходимо просуммировать энергии всех его элементов:

(2)

или , (3)

т.к. линейная скорость вращения связана с угловой скоростью u_i=wr_i.

Поскольку угловая скорость w одинакова для всех элементов тела, ее можно вынести за знак суммы:

. (4)

Величина называется моментом инерции твердого тела, а - моментом инерции одного элемента (материальной точки), размерами которого можно пренебречь по сравнению с его радиусом вращения. Момент инерции тела равен сумме моментов инерции элементов, составляющих это тело:

. (5)

Тогда формула для кинетической энергии вращательного движения твердого тела принимает вид:

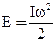. (6)

Момент инерции не зависит от скорости вращения тела и характеризует инертность тела при вращательном движении: чем больше I, тем большую энергию надо затратить для достижения заданной угловой скорости. Это следует из формулы (6). Значение момента инерции определяется не только массой тела, но и ее распределением относительно оси вращения. Для тонкостенного полого цилиндра (толщина которого много меньше его радиуса R) момент инерции, согласно (5), будет равен:

. (7)

В случае непрерывного распределения массы сумма в определении (5) сводится к интегралу:

, (8)

где dm – масса материальной точки тела, r - плотность в определенной точке тела, dV – элементарный объем. Интегрирование производится по всему объему тела.

В качестве примера рассчитаем момент инерции сплошного цилиндра высотой h относительно его геометрической оси. Для этого разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r (рис.4).

Рис.4.

Так как радиусы точек бесконечно тонкого цилиндра равны между собой, то его момент инерции можно рассчитать по формуле:

, (9)

где dm – масса всего элементарного цилиндра. Выразим массу полого элементарного цилиндра через его объем dV и плотность r:

. (10)

Следовательно, момент инерции элементарного цилиндра равен:

, (11)

а всего цилиндра:

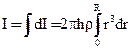, (12)

где R – радиус цилиндра. Производя интегрирование и подставив пределы, получим:

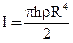. (13)

Но phR² - объем цилиндра, а его масса m=rV=phrR². Тогда его момент инерции равен:

. (14)

Без расчета приведем формулы моментов инерции однородного шара относительно оси, проходящей через его центр:

(15)

и для однородного стержня относительно перпендикулярной ему оси, проходящей через его центр:

, (16)

где l – длина стержня, R – радиус шара, m – массы этих тел.

Для расчета момента инерции тела относительно оси, не проходящей через его центр масс, нужно воспользоваться теоремой Штейнера, которая формулируется следующим образом: Момент инерции относительно произвольной оси равен моменту инерции I₀ относительно оси, параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния, между осями:

. (17)

Не нашли, что искали? Воспользуйтесь поиском: