Понятие матрицы передаточной функции

Введение векторных переменных позволяет для линейных систем использовать привычный аппарат передаточных функций и структурных схем, однако понятие передаточной функции значительно расширяется.

Пусть имеется многомерная система управления со структурной схемой показанной на рис. 1.2. и системой дифференциальных уравнений, записанных в

символической форме.

Рис.1.2

По аналогии с одномерными системами можно записать:

(1.8)

где Q(p)-квадратная матрица операторных коэффициентов размера n на n:

R(p)- прямоугольная матрица операторных коэффициентов размера n на k:

S(p)- прямоугольная матрица операторных коэффициентов размера n на l:

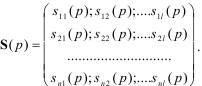
Для получения системы дифференциальных уравнений необходимо перемножить прямоугольную или квадратную матрицы на матрицы - столбцы соответствующих переменных объекта.

Взаимосвязь уравнений состояния с уравнениями системы в виде (1.8)

определяется из следующих соотношений. Из второго уравнения (1.7) выразим переменную x (t) через y(t):

(1.9)

и подставим это выражение в первое уравнение (1.7):

(1.10)

Преобразовывая по Лапласу (1.10) и группируя подобные члены, получим

выражение аналогичное (1.8), которое путем приравнивания матриц при одноименных переменных позволяет установить взаимосвязь (1.7) с (1.8).

(1.11)

где I – единичная матрица,

По аналогии с одномерными системами, используя основные правила

теории матриц, можно ввести понятие матриц передаточной функции, временных и частотных характеристик.

Если умножить (1.8) на обратную матрицу 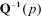, то получим:

(1.12)

Отсюда можно получить выражение для матриц передаточных функций

системы по управлению

(1.13)

и возмущению

(1.14)

Из теории матриц известно, что обратная матрица может быть вычислена по методу неопределенных коэффициентов применительно к выражению:

где I - единичная матрица, что в конечном итоге приводит к решению систем линейных алгебраических уравнений.

Второй способ вычисления обратной матрицы задаётся выражением:

(1.15)

Если в матрице передаточной функции для каждого элемента матрицы

найти обратное преобразование Лапласа, то получится матрица весовых функций (матрица Коши).

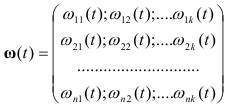(1.16)

Если в момент времени t=0 на все к входов поступают управляющие воздействия u(t), то изменение i- ой регулируемой величины может быть найдено посредством интеграла Дюамеля на основании принципа суперпозиции:

(1.17)

Аналогично одномерным системам, производя замену оператора p на оператор jω для каждого элемента матрицы передаточных функций (1.13), (1.14), получим матрицу комплексной передаточной функции.

(1.18)

Если теперь положить, что одновременно на все входы многомерной систе-

мы поступают гармонические сигналы одинаковой частоты ω, то АЧХ и ФЧХ i-ой регулируемой величины могут быть вычислены по следующим формулам:

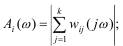
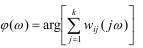
Т. е. сначала определяют частотную передаточную функцию по i- ому вы-

ходу как сумму комплексных элементов j- ой строки матрицы частотной передаточной функции всей системы, а затем АЧХ и ФЧХ находят как модуль и аргумент этой суммы комплексных элементов.

Также как и для одномерных систем, в многомерных системах одной и той же матрице передаточной функции может соответствовать несколько вариантов структурных схем и уравнений состояния. Т.е. по уравнениям состояния матрица

передаточной функции может быть получена однозначно, обратное утверждение

будет неверным.

Не нашли, что искали? Воспользуйтесь поиском: