Матричная запись метода узловых напряжений

На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:

,

(14)

где - диагональная матрица проводимостей ветвей, все члены которой, за исключением элементов главной диагонали, равны нулю.

Матрицы Z и Y взаимно обратны.

Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому

,

(15)

получим:

..

(16)

Выражение (16) перепишем, как:

.

(17)

Принимая потенциал узла, для которого отсутствует строка в матрице А, равным нулю, определим напряжения на зажимах ветвей:

.

(18)

Тогда получаем матричное уравнение вида:

.

(19)

Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить

(20)

,

(21)

то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:

(22)

где - матрица узловых проводимостей; 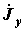- матрица узловых токов.

В развернутом виде соотношение (22) можно записать, как:

(23)

то есть получили известный из метода узловых потенциалов результат.

Рассмотрим составление узловых уравнений на примере схемы по рис. 4.

Данная схема имеет 3 узла (m=3) и 5 ветвей (n=5). Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.

Узловая матрица (примем )

А

Диагональная матрица проводимостей ветвей:

Y

,

где .

Матрица узловых проводимостей

.

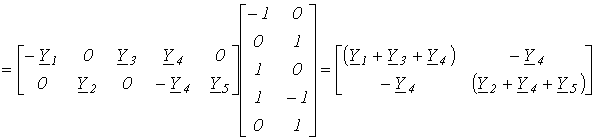Матрицы токов и ЭДС источников

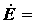
..Следовательно, матрица узловых токов будет иметь вид:

.Таким образом, окончательно получаем:

,

где ; ; ; ; .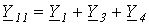

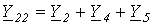Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.

16) Теорема наложения и метод расчёта, основанный на ней

Данный метод справедлив только для линейных электрических цепей и является особенно эффективным, когда требуется вычислить токи для различных значений ЭДС и токов источников в то время, как сопротивления схемы остаются неизменными.

Данный метод основан на принципе наложения (суперпозиции), который формулируется следующим образом: ток в k – й ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников в отдельности.

Аналитически принцип наложения для цепи, содержащей n источников ЭДС и m источников тока, выражается соотношением

.

(1)

Здесь - комплекс входной проводимости k – й ветви, численно равный отношению тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях; - комплекс взаимной проводимости k – й и i– й ветвей, численно равный отношению тока в k – й ветви и ЭДС в i– й ветви при равных нулю ЭДС в остальных ветвях.

Входные и взаимные проводимости можно определить экспериментально или аналитически, используя их указанную смысловую трактовку, при этом , что непосредственно вытекает из свойства взаимности (см. ниже).

Аналогично определяются коэффициенты передачи тока , которые в отличие от проводимостей являются величинами безразмерными.

Доказательство принципа наложения можно осуществить на основе метода контурных токов.

Если решить систему уравнений, составленных по методу контурных токов, относительно любого контурного тока, например , то получим

,

(2)

где - определитель системы уравнений, составленный по методу контурных токов; - алгебраическое дополнение определителя .

Каждая из ЭДС в (2) представляет собой алгебраическую сумму ЭДС в ветвях i–го контура. Если теперь все контурные ЭДС в (2) заменить алгебраическими суммами ЭДС в соответствующих ветвях, то после группировки слагаемых получится выражение для контурного тока в виде алгебраической суммы составляющих токов, вызванных каждой из ЭДС ветвей в отдельности. Поскольку систему независимых контуров всегда можно выбрать так, что рассматриваемая h-я ветвь войдет только в один -й контур, т.е. контурный ток будет равен действительному току h-й ветви, то принцип наложения справедлив для токов любых ветвей и, следовательно, справедливость принципа наложения доказана.

Таким образом, при определении токов ветвей при помощи метода наложения следует поочередно оставлять в схеме по одному источнику, заменяя остальные их внутренними сопротивлениями, и рассчитать составляющие искомых токов в этих схемах. После этого полученные результаты для соответствующих ветвей суммируются – это и будут искомые токи в ветвях исходной цепи.

В качестве примера использования метода наложения определим ток во второй ветви схемы на рис. 1,а.

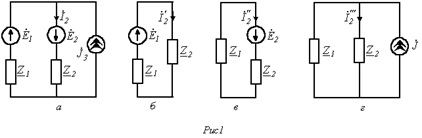
Принимая источники в цепи на рис. 1,а идеальными и учитывая, что у идеального источника ЭДС внутреннее сопротивление равно нулю, а у идеального источника тока – бесконечности, в соответствии с методом наложения приходим к расчетным схемам на рис. 1,б…1,г.

В этих цепях

; ; ,

где ; ; .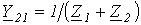

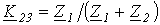Таким образом,

.

В качестве другого примера использования метода определим взаимные проводимости и 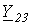в цепи на рис. 2, если при переводе ключа в положение 1 токи в первой и второй ветвях соответственно равны 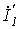и , а при переводе в положение 2 - и .

Учитывая, что в структуре пассивного четырехполюсника не содержится источников энергии, на основании принципа наложения для состояния ключа в положении “1” можно записать

;

(3)

.

(4)

При переводе ключа в положение “2” имеем

;

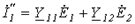(5)

..

(6)

Тогда, вычитая из уравнения (3) соотношение (5), а из (4)-(6), получим

;

,

откуда искомые проводимости

; .

17) Теорема об эквивалентном генераторе и метод расчёта, основанный на ней

Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.

Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Ход доказательства теоремы иллюстрируют схемы на рис. 1.

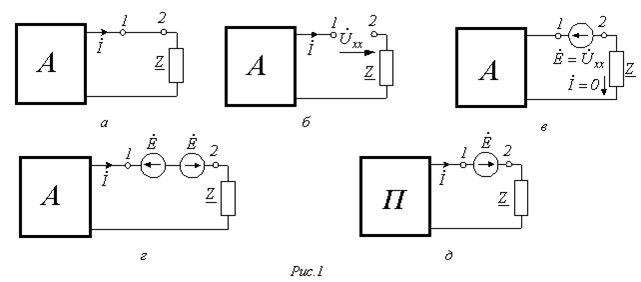
Пусть в схеме выделена некоторая ветвь с сопротивлением Z, а вся оставшаяся цепь обозначена как активный двухполюсник А (рис. 1,а). Разомкнем эту ветвь между точками 1 и 2 (рис. 1,б). На зажимах этой ветви имеет место напряжение . Если теперь между зажимами 1 и 2 включить источник ЭДС с направлением, указанным на рис. 1,в, то, как и в цепи на рис.1,б ток в ней будет равен нулю. Чтобы схему на рис. 1,в сделать эквивалентной цепи на рис. 1,а, в рассматриваемую ветвь нужно включить еще один источник ЭДС 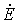, компенсирующий действие первого (рис. 1,г). Будем теперь искать ток по принципу наложения, т.е. как сумму двух составляющих, одна из которых вызывается источниками, входящими в структуру активного двухполюсника, и источником ЭДС 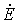, расположенным между зажимами 1 и 2 слева, а другая – источником ЭДС 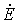, расположенным между зажимами 1 и 2 справа. Но первая из этих составляющих в соответствии с рис. 1,в равна нулю, а значит, ток определяется второй составляющей, т.е. по схеме на рис. 1,д, в которой активный двухполюсник А заменен пассивным двухполюсником П. Таким образом, теорема доказана.

Указанные в теореме ЭДС и сопротивление можно интерпретировать как соответствующие параметры некоторого эквивалентного исходному активному двухполюснику генератора, откуда и произошло название этого метода.

Таким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б.

Отсюда ток находится, как:

,

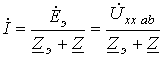(1)

где 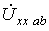- напряжение на разомкнутых зажимах a-b.

Уравнение (1) представляет собой аналитическое выражение метода эквивалентного генератора.

Параметры эквивалентного генератора (активного двухполюсника) могут быть определены экспериментальным или теоретическим путями.

В первом случае, в частности на постоянном токе, в режиме холостого хода активного двухполюсника замеряют напряжение на его зажимах с помощью вольтметра, которое и равно . Затем закорачивают зажимы a и b активного двухполюсника с помощью амперметра, который показывает ток (см. рис. 2,б). Тогда на основании результатов измерений .

В принципе аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо определить комплексные значения и .

При теоретическом определении параметров эквивалентного генератора их расчет осуществляется в два этапа:

1. Любым из известных методов расчета линейных электрических цепей определяют напряжение на зажимах a-b активного двухполюсника при разомкнутой исследуемой ветви.

2. При разомкнутой исследуемой ветви определяется входное сопротивление активного двухполюсника, заменяемого при этом пассивным. Данная замена осуществляется путем устранения из структуры активного двухполюсника всех источников энергии, но при сохранении на их месте их собственных (внутренних) сопротивлений. В случае идеальных источников это соответствует закорачиванию всех источников ЭДС и размыканию всех ветвей с источниками тока.

Сказанное иллюстрируют схемы на рис. 3, где для расчета входного (эквивалентного) сопротивления активного двухполюсника на рис. 3,а последний преобразован в пассивный двухполюсник со структурой на рис. 3,б. Тогда согласно схеме на рис. 3,б

.

В качестве примера использования метода эквивалентного генератора для анализа определим зависимость показаний амперметра в схеме на рис. 4 при изменении сопротивления R переменного резистора в диагонали моста в пределах . Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60 Ом.

В соответствии с изложенной выше методикой определения параметров активного двухполюсника для нахождения значения перейдем к схеме на рис. 5, где напряжение на разомкнутых зажимах 1 и 2 определяет искомую ЭДС . В данной цепи

.

Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рис. 6.

Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно:

.

Таким образом, для показания амперметра в схеме на рис. 4 в соответствии с (1) можно записать

.

(2)

Задаваясь значениями R в пределах его изменения, на основании (2) получаем кривую на рис.7.

В качестве примера использования метода эквивалентного генератора для анализа цепи при синусоидальном питании определим, при каком значении нагрузочного сопротивления в цепи на рис. 8 в нем будет выделяться максимальная мощность, и чему она будет равна.

Параметры цепи: ; .

В соответствии с теоремой об активном двухполюснике обведенная пунктиром на рис. 8 часть схемы заменяется эквивалентным генератором с параметрами

В соответствии с (1) для тока через можно записать

откуда для модуля этого тока имеем

. (3)

Анализ полученного выражения (3) показывает, что ток I, а следовательно, и мощность будут максимальны, если ; откуда , причем знак “-” показывает, что нагрузка имеет емкостный характер.

Таким образом,

и .

Данные соотношения аналогичны соответствующим выражениям в цепи постоянного тока, для которой, как известно, максимальная мощность на нагрузке выделяется в режиме согласованной нагрузки, условие которого .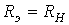

Таким образом, искомые значения и максимальной мощности: .

18) Теорема взаимности и метод расчёта, основанный на ней

Принцип взаимности основан на теореме взаимности, которую сформулируем без доказательства: для линейной цепи ток 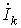в k – й ветви, вызванной единственной в схеме ЭДС , находящейся в i – й ветви,

будет равен току в i – й ветви, вызванному ЭДС , численно равной ЭДС , находящейся в k – й ветви,

.

Отсюда в частности вытекает указанное выше соотношение .

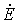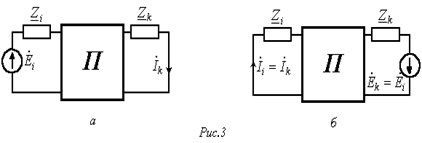
Иными словами, основанный на теореме взаимности принцип взаимности гласит: если ЭДС , действуя в некоторой ветви схемы, не содержащей других источников, вызывает в другой ветви ток (см. рис. 3,а), то принесенная в эту ветвь ЭДС 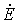вызовет в первой ветви такой же ток (см. рис. 3,б).

В качестве примера использования данного принципа рассмотрим цепь на рис. 4,а, в которой требуется определить ток , вызываемый источником ЭДС .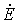

Перенесение источника ЭДС 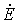в диагональ моста, где требуется найти ток, трансформирует исходную схему в цепь с последовательно-параллельным соединением на рис. 4,б. В этой цепи

,

(7)

где .

В соответствии с принципом взаимности ток в цепи на рис. 4,а равен току, определяемому соотношением (7).

Не нашли, что искали? Воспользуйтесь поиском: