Проверка гипотез о параметрах нормального распределения в одновыборочной совокупности

Рассмотрим случай, когда выборка 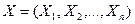получена из нормального распределения , в котором один или оба параметра распределения неизвестны. Будем строить двусторонние критерии значимости для проверки простой гипотезы 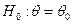против сложной альтернативы . Кроме этого, будут указаны и критические области для односторонних критериев.

1) Пусть выборка 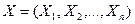получена из распределения с неизвестным математическим ожиданием и известной дисперсией . Рассматривается гипотеза против альтернативы . Ранее уже был получен доверительный интервал для с уровнем доверия вида . Тогда критическая область определяется как множество точек, для которых не принадлежит указанному доверительному интервалу. В результате этого получим критерий проверки гипотезы : принять эту гипотезу на уровне значимости 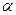, если попадает в указанный выше доверительный интервал.

Для альтернативы 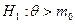получим односторонний критерий значимости с областью принятия гипотезы вида: . Очевидно, для альтернативы имеем: .

2) Пусть выборка 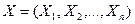получена из распределения 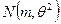с известным математическим ожиданием 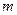и неизвестной дисперсией . Рассматривается гипотеза против альтернативы . Из примера 2 выше была получена критическая область для одностороннего критерия с альтернативой вида: 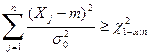. Введем здесь статистику . Тогда область принятия гипотезы для двусторонней альтернативы будет иметь вид: .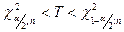

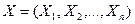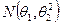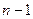3) Пусть выборка получена из распределения с неизвестным математическим ожиданием и неизвестной дисперсией . Рассматривается гипотеза против двусторонней альтернативы . В качестве статистики критерия возьмем величину , в которой в качестве оценки дисперсии используется величина . Тогда случайная величина будет иметь распределение Стьюдента с степенями свободы. Тогда область принятия гипотезы для двусторонней альтернативы будет иметь вид: 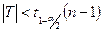, где – квантиль распределения Стьюдента с 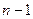степенями свободы на уровне .

4) Пусть выборка 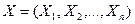получена из распределения 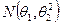с неизвестным математическим ожиданием и неизвестной дисперсией . Рассматривается гипотеза против двусторонней альтернативы . В качестве статистики критерия возьмем величину 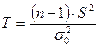. Случайная величина имеет распределение "хи-квадрат" с 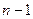степенями свободы. Тогда область принятия гипотезы для двусторонней альтернативы будет иметь вид: , где – квантиль распределения "хи-квадрат" с 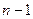степенями свободы на уровне .

Не нашли, что искали? Воспользуйтесь поиском: