Рассмотрим вторую позиционную задачу: построение линии пересечения двух плоскостей.

Кафедра графики

УТВЕРЖДАЮ

Проректор по УР

А.А. Патрушев

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ИЗУЧЕНИЮ КУРСА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Челябинск, 2008

Методические указания к изучению курса начертательной геометрии и инженерной графики предназначены для студентов I курса всех факультетов дневного обучения, начинающих изучать инженерную графику и начертательную геометрию. Конспект составлен авторами на основании многолетнего опыта чтения лекций в ЧГАУ и включает основные вопросы разделов и тем начертательной геометрии.

Составители:

Торбеев И.Г. – доц., к.т.н., зав. кафедрой инженерной графики и начертательной геометрии (ЧГАУ)

Ружинская Т.М. - старший преподаватель (ЧГАУ)

Рецензенты:

Четыркин Ю.Б. – доц., к.т.н. (ЧГАУ)

Ответственный за выпуск:

Торбеев И.Г. – доц.,к.т.н., зав. кафедрой инженерной графики и начертательной геометрии

Печатается по решению издательского совета ЧГАУ

Ó Челябинский Государственный Агроинженерный Университет, 2008 г.

1. Предмет начертательной геометрии.

Начертательная геометрия - раздел геометрии, в котором изучаются пространственные фигуры при помощи построения их изображений на плоскости, а также методы решения и исследования пространственных задач на плоском чертеже.

Построение чертежей производится по одному из способов проецирования. Эти способы излагает и обосновывает начертательная геометрия. В связи с этим, предметом начертательной геометрии являются:

1. Создание методов изображения геометрических фигур на плоскости;

2. Изучение геометрических свойств фигур по их изображениям (чтение чертежа);

3. Разработка способов графического решения на плоскости различных пространственных задач, относящихся к пространственным фигурам (позиционных и метрических задач).

Многие положения начертательной геометрии основаны на соответствующих теоремах стереометрии. Особенностью изучения курса является тесная взаимосвязь последующего материала с предыдущим. При изложении материала в данном методическом пособии принята определенная система обозначений, которую нужно изучить самостоятельно. Следует знать: как обозначаются точки пространства, прямые и кривые линии, плоскости и поверхности, плоскости проекций, углы, условные знаки сокращенной записи, заменяющие отдельные наиболее часто встречающиеся слова и выражения.

2. Метод проекций. Виды проекций.

Для построения изображений геометрических фигур на плоскости пользуются методом проецирования.

Проекция - это отображение геометрической фигуры на плоскость проекций.

Рассмотрим на примере аппарат проецирования. Пусть даны точка S-центр проецирования, плоскость П - плоскость проекции, и точка А - геометрический объект, изображение которого нужно построить (рис.1). Для построения изображения (проекции) точки А строят проецирующую прямую SA и определяют точку А¢ пересечения прямой SA с плоскостью П. Точку А¢ называют проекцией точки А.

В зависимости от расположения центра проецирования S и плоскости проекций П проецирование может быть центральным, если центр проецирования расположен на фиксированном расстоянии от плоскости, или параллельным (частный случай центрального), если центр проецирования удален от плоскости проекций в бесконечность.

При параллельном проецировании обычно вместо конкретного центра проецирования S задают направление проецирования. Так как проецирующие линии (лучи) в этом случае параллельны, то они составляют с плоскостью проекций один и тот же угол. Если этот угол a не равен 90°, то такое параллельное проецирование называется косоугольным. В случае, когда проецирующие лучи перпендикулярны плоскости проекции,Ða=90°- параллельное проецирование называется прямоугольным или ортогональным.

Таким образом, прямоугольное проецирование является частным случаем параллельного проецирования и является основным методом построения чертежей.

Так как одна проекция объекта проецирования (точки, прямой, плоскости или поверхности) не определяет его положения в пространстве, для определения положения объекта необходимо иметь не менее двух его проекций. С этой целью строят прямоугольные проекции объектов на две или три взаимно перпендикулярные плоскости проекций (рис.2).

3. Инвариантные свойства ортогонального (прямоугольного) проецирования.

При параллельном ортогональном проецировании, в общем случае, нарушается метрическое равенство между оригиналом и его проекцией, хотя проекция сохраняет некоторые свойства оригинала, которые называются инвариантными (неизменяемыми).

1. Проекция точки есть точка:

А®А_п

2. Проекция прямой на плоскость есть прямая:

L(AB)®L_п(A_пB_п)

3. Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии:

АÎLÞA_пÎL_п

4. Проекции взаимно çç прямых также взаимно çç, а отношение отрезков таких прямых равно отношению их çç проекций.

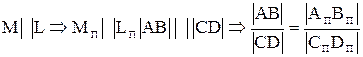
5. Точка пересечения, проекций пересекающихся прямых является проекцией точки пересечения этих прямых:

аÇb=MÞa_пÇb_п=М_п

6. Плоская фигура, параллельная плоскости проекции проецируется на эту плоскость без искажений.

7. Плоский прямоугольник в общем случае проецируется в многоугольник с тем же числом вершин. Если плоскость многоугольника параллельна направлению проецирования, то она проецируется в прямую линию.

8. Параллельный перенос оригинала или плоскости проекций не изменяет вида и размеров проекций оригинала.

9. Если хотя бы одна из сторон прямого угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол проецируется без искажений.

4. Точка.

Прямоугольной проекцией точки на плоскость называется основание перпендикуляра, опущенного из точки на плоскость проекции.

В качестве плоскостей проекций берут три взаимно перпендикулярные плоскости П₁,П₂, П₃ (рис. 3).

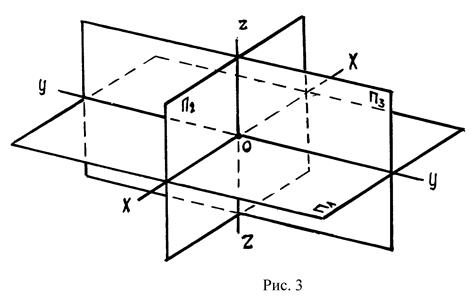
Плоскость П₁ называется горизонтальной плоскостью проекций.

Плоскость П₂ называется фронтальной плоскостью проекций.

Плоскость П₃ называется профильной плоскостью проекций.

Пересечение горизонтальной плоскости с фронтальной принимается за ось X.

Пересечение горизонтальной плоскости с профильной – ось Y.

Пересечение фронтальной плоскости с профильной – ось Z.

Место пересечения трех осей обозначается т. О и называется центром или началом координат.

Для точки А (рис. 4) проецирующие линии: АА₁^П₁, АА₂^П₂, АА₃^П₃.

Остальные линии – это линии связи проекций. Проекция на П₁ называется горизонтальной проекцией, проекция на П₂ – фронтальной проекцией, на П₃ – профильной.

Для удобства и простоты пользования при решении задач от трехгранника образованного плоскостями П₁,П₂ и П₃ необходимо перейти к комплексному чертежу.

Комплексным чертежом называется чертеж, составленный из нескольких связанных между собой проекций геометрического объекта.

Для получения комплексного чертежа следует совместить плоскость П₁ и П₃ с плоскостью П₂, вращая их вокруг соответствующих осей (рис.5). Для этого трехгранник образованный плоскостями П₁, П₂, П₃ разрезать вдоль оси Y.

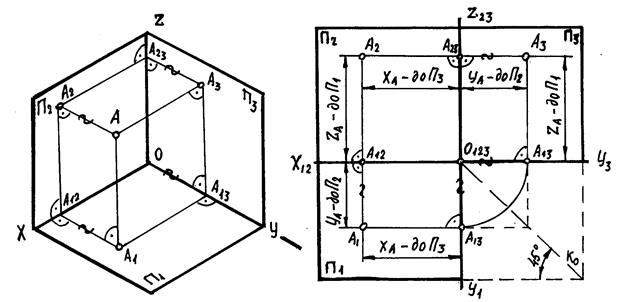
Рис. 4 Рис. 5

При этом убирается точка А и проецирующие линии. Ось X на комплексном чертеже обозначается X₁₂, т.к. она принадлежит одновременно двум плоскостям проекции: П₁ и П₂. Ось Z обозначается Z₂₃, т.к. она принадлежит П₂ и П₃. Ось Y на П₁ обозначается Y₁, на П₃ – Y₃. Центр координат на комплексном чертеже обозначается О₁₂₃.

Фронтальная и горизонтальная проекции точки располагаются на одной вертикальной линии связи – А₁А₂^X₁₂.

Фронтальная и профильная проекция точки расположены на одной линии связи – А₂А₃^Z₂₃. При наличии двух проекций точки, третью проекцию можно найти с помощью прямой К_о, которая называется постоянной прямой комплексного чертежа.

Определение пространственного положения точки можно осуществлять при помощи её прямоугольных координат.

Координатами точки являются числа, выражающие расстояние от точки до трех взаимно перпендикулярных плоскостей проекции П₁,П₂,П₃.

Расстояние от точки А до профильной плоскости проекции (П₃) называется широтой (X_а):

X_а=АА₃=А₂А₂₃=А₁А₁₃

Широта точки читается на плоскостях проекций П₁ и П₂. Расстояние от точки А до фронтальной плоскости проекций (П₂) называется глубиной (Y_а):

Y_а=АА₂=А₁А₁₂=А₃А₂₃

Глубина точки читается на плоскостях проекций П₁ и П₃. Расстояние от точки А до горизонтальной плоскости проекций (П₁) называется высотой (Z_а):

Z_а=АА₁=А₂А₁₂=А₃А₁₃

Высота точки читается на плоскости проекций П₂ и П₃.

При прямоугольном проецировании возможны случаи, когда две точки имеют одинаковую координату. В этом случае на двух плоскостях проекций они лежат на одной линии связи, а на третьей плоскости проекций – проекции этих точек совпадают (одна из них закрывается другой). Такие точки называются конкурирующими точками.

Конкурирующие точки могут быть на П₁, П₂ и П₃. В каждом из этих случаев важно знать условия видимости конкурирующих точек. Итак:

А. Из двух горизонтально конкурирующих точек на П₁ видна та, которая выше (у которой больше высота).

В. Из двух фронтально конкурирующих точек на П₂ видна та, которая ближе (у которой больше глубина).

С. Из двух профильно конкурирующих точек на П₃ видна та, у которой больше широта.

5. Прямая.

Прямая определяется в пространстве двумя точками А и В, а её проекции на плоскость определяется проекциями этих точек.

Если прямая не параллельна и не перпендикулярна ни одной из плоскостей проекций, то такая прямая называется прямой общего положения.

Прямая общего положения может быть восходящей, если по мере удаления от наблюдателя поднимается вверх, может быть нисходящей – если по мере удаления от наблюдателя опускается вниз.

О положении отрезка АВ в пространстве можно судить по координатам точек А и В до плоскости проекций, но можно определить разность этих расстояний, т.е. можно судить о расположении точек А и В относительно друг друга (рис. 6). Тогда рассматриваются разности координат: разность широт X_а-X_в, разность глубин Y_a-Y_в, разность высот Z_a-Z_в. Такие координаты называются относительными. При построении такого чертежа положение двух проекций одной из точек выбирается произвольно (А₁ и А₂ на одной вертикальной линии связи), проекции остальных точек строят, учитывая известные разности координат, которые могут положительными или отрицательными (рис.7). Такой чертеж называется безосным. На безосном чертеже т. А выполняет функцию т. О – начала координат в осной системе, от которой ведётся отсчет разности координат для построения проекций других точек.

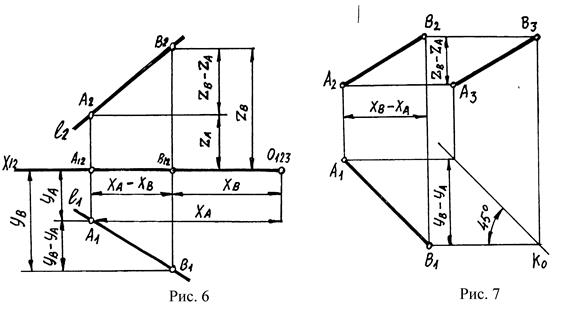
Пример. Построить проекции отрезка АВ, если известны координаты т. В, вычисленные относительно т. А. Положение т. В определяется заданными разностями координат: ½X_в-X_а½, ½Y_в-Y_а½, ½Z_в-Z_а½.

Решение:

1. Произвольно задаем положение т. А (А₁, А₂) на вертикальной линии связи.

2. Проводим вторую вертикальную линию связи для т. В, учитывая ½X_в-X_а½, если эта разность положительная, то величина её откладывается влево от линии связи А₂А₁, если величина отрицательная, то вправо.

3. Фронтальная проекция т. В (В₂) определяется по величине ½Z_в-Z_а½ в зависимости от положительной или отрицательной её величины (если величина положительная, то ½Z_в-Z_а½ откладывается вверх, если отрицательная – вниз).

4. Горизонтальная проекция т. В (В₁) определяется по величине ½Y_в-Y_а½ учитывая отрицательный или положительный знак разности глубин (отрицательная величина разности глубин откладывается вверх, положительная – вниз).

5. Соединив одноименные проекции А₂В₂ и А₁В₁ прямыми линиями, получим искомые проекции АВ.

Прямые в пространстве могут занимать разные положения относительно плоскостей проекций П₁,П₂,П₃.

Прямая, расположенная параллельно какой-либо плоскости проекций, называется прямой уровня.

На комплексном чертеже различают три линии уровня (см. таблицу 1):

1. Горизонтальная прямая уровня (горизонталь) – прямая параллельная П₁.

Обозначается обычно буквой h. Все точки горизонтали имеют равные высоты. На П₁ прямая h проецируется в натуральную величину (т.е. без искажений). Проекция горизонтали на П₂ перпендикулярна вертикальным линиям связи. Угол наклона горизонтали к плоскости П₂ (b) проецируется на П₁ без искажений.

2. Фронтальная прямая уровня (фронталь) – прямая параллельная П₂.

3. Обозначается обычно f (f₁, f₂). Все точки фронтали имеют равные глубины. На П₂ прямая f проецируется в натуральную величину. Проекция фронтали на П₁ перпендикулярна вертикальным линиям связи. Угол наклона фронтали к плоскости П₁ (a) проецируется на П₂ без искажений.

4. Профильная линия уровня – прямая, параллельная П₃.

Обозначается буквами EF (E₁F₁, E₂F₂, E₃F₃). Все точки профильной прямой имеют равные широты. На П₁ и П₂ проекция профильной прямой лежат на одной вертикальной линии связи. На П₃ профильная прямая проецируется в натуральную величину, а также на П₃ без искажения проецируются углы наклона прямых к П₁ и П₂ (a и b).

Таблица 1

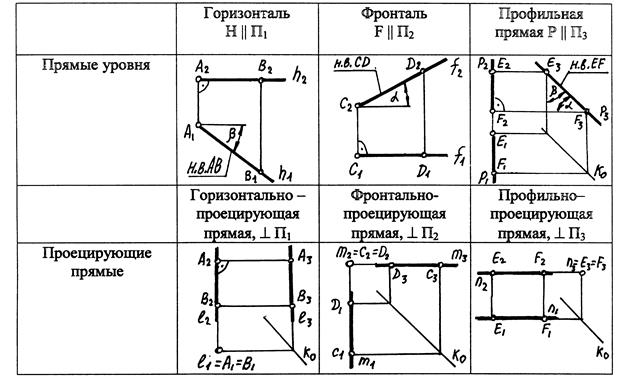
Прямая, расположенная перпендикулярно какой-либо плоскости проекций, называется проецирующей прямой. На комплексном чертеже различают три проецирующие прямые:

1. Горизонтально – проецирующая прямая – прямая, перпендикулярная П₁.

Так как, П₁, П₂ и П₃ взаимно перпендикулярны, то прямая, перпендикулярная П₁ в то же время параллельна П₂ и П₃. На П₁ прямая проецируется в точку. На П₂ и П₃ прямая проецируется в натуральную величину, проекция прямой на П₂ и П₃ параллельна вертикальным линиям связи.

2. Фронтально – проецирующая прямая – прямая, перпендикулярная П₂ и параллельная П₁ и П₃. На П₂ прямая проецируется в точку. На П₁ прямая проецируется в натуральную величину, а проекция на П₁ параллельна вертикальным линиям вязи. На П₃ прямая так же проецируется в натуральную величину, а проекция прямой на П₃ параллельна линиям связи.

3. Профильно – проецирующая прямая – прямая, перпендикулярная П₃ и параллельная П₁ и П₂. На П₃ проецируется в точку, на П₁ и П₂ проецируется в натуральную величину и перпендикулярна вертикальным линиям связи.

Таким образом, можно видеть, что прямые уровня и проецирующие прямые на комплексном чертеже всегда имеют одну проекцию, равную натуральной величине отрезка. Несложно так же определить угол наклона таких прямых к плоскости проекций.

Для определения натуральной величины прямой общего положения и угла наклона её к плоскостям проекций, пользуются способом прямоугольного треугольника (рис. 8 а, б, в).

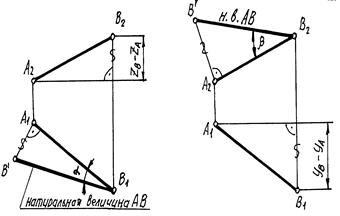
Рис. 8а Рис. 8б Рис. 8в

Строится прямоугольный треугольник, у которого один катет – это проекция прямой на П₁, второй катет – это разность высот точек отрезка. Результат – гипотенуза такого треугольника – это натуральная величина отрезка, а угол между проекцией на П₁ и натуральной величиной – это угол наклона прямой к П₁ (Ða).

Прямоугольный треугольник можно построить и на П₂. В этом случае один катет будет проекцией отрезка на П₂, второй катет – разность глубин точек отрезка, гипотенуза – натуральная величина, угол между проекцией на П₂ и натуральной величиной – угол наклона прямой к П₂ (Ðb).

Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися:

1. Если две прямые параллельны в пространстве, то на комплексном чертеже их одноименные проекции тоже параллельны между собой. Верно так же и обратное утверждение: если на комплексном чертеже горизонтальные, а также фронтальные проекции двух прямых попарно параллельны, то и прямые в пространстве параллельны.

2. Если прямые пересекаются в пространстве, то и на комплексном чертеже их одноименные проекции пересекаются в точке, лежащей на одной линии связи, так как две пересекающиеся прямые в пространстве имеют общую точку.

3. Две скрещивающиеся прямые в пространстве не имеют общей точки. Поэтому точки пересечения их горизонтальных и фронтальных проекций на комплексном чертеже не лежат на одной линии связи. Эти точки являются конкурирующими, применяются для определения видимости при построении взаимного положения двух фигур.

При пересечении двух прямых образуются углы, которые проецируются на любую плоскость проекций без искажений в случае, если обе прямые лежат в плоскости, параллельной плоскости проекций. Если две прямые пересекаются под прямым углом, то следует знать, что проецирование прямого угла имеет особое свойство.

Если одна из сторон прямого угла параллельна одной из плоскостей проекций, то прямой угол проецируется на эту плоскость без искажений (инвариантные свойства параллельного проецирования).

6. Плоскость.

Проекцией любой плоскости является геометрическое место проекций всех её точек. Если рассматривать плоскость, расположенную не перпендикулярно ни одной из плоскостей проекций, то её проекции целиком заполняют поля плоскостей проекций П₁, П₂, П₃. Поэтому на комплексном чертеже задаются лишь некоторые геометрические элементы, определяющие положение заданной плоскости в пространстве:

1. три точки принадлежащие плоскости и не лежащие ни на одной прямой;

2. прямая и точка (не лежащие на прямой);

3. две параллельные прямые;

4. две пересекающиеся прямые;

5. любая плоская фигура. (рис.9)

При решении задач по начертательной геометрии, связанных с плоскостью, важно знать в каких случаях прямая принадлежит плоскости.

Прямая принадлежит плоскости в двух случаях:

1. Если она проходит через две точки, принадлежащие этой плоскости.

2. Если она проходит через точку, принадлежащую плоскости, и параллельна прямой, находящейся в этой плоскости.

В обоих случаях при задании прямой в плоскости необходимо иметь точки принадлежащие этой плоскости. Поэтому важно знать, в каком случае, что точка принадлежит плоскости.

Точка принадлежит плоскости, если через неё можно провести прямую, принадлежащую этой плоскости.

В любой плоскости есть прямые, которые называются особыми прямыми на плоскости. К таким прямым относятся горизонтали плоскости, фронтали плоскости и линии наибольшего наклона к плоскостям проекций.

Горизонталь плоскости – прямая, лежащая в плоскости и параллельная плоскости проекции П1.

Фронтальная проекция горизонтали плоскости перпендикулярна к вертикальным линиям связи и параллельна оси X.

Фронталь плоскости – прямая, принадлежащая плоскости и параллельная плоскости проекций П2.

Горизонтальная проекция фронтали плоскости перпендикулярна к вертикальным линиям связи и параллельна оси X (рис.10).

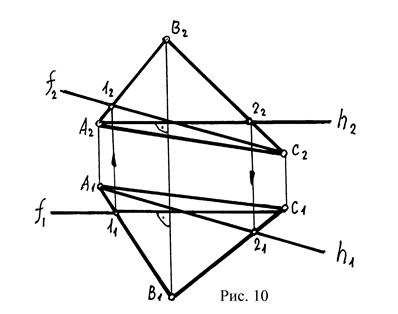
Линии наибольшего наклона к плоскости проекций – это прямые, лежащие в данной плоскости и образующие с одной из плоскостей проекций наибольший угол.

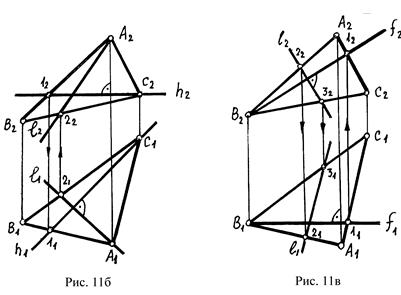
Линия наибольшего наклона к П1 называется линией ската. Линия ската (l) данной плоскости должна быть перпендикулярна к горизонтали (h) этой плоскости (рис. 11а,б). На комплексном чертеже горизонтальная проекция линии ската перпендикулярна к горизонтальной проекции горизонтали плоскости.

Линия наибольшего наклона к П2 перпендикулярна к фронтали плоскости (рис.11в). Её фронтальная проекция перпендикулярна к фронтальной проекции фронтали плоскости.

Так же как и прямая, плоскость может занимать различные положения относительно плоскостей проекций.

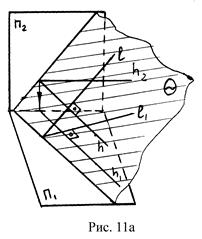
Плоскость не перпендикулярна и не параллельна ни одной из плоскостей проекций – плоскость общего положения.

Плоскость перпендикулярна какой-либо плоскости проекций – проецирующая плоскость.

Плоскость параллельна какой-либо плоскости проекций – плоскость уровня.

Всего на комплексном чертеже рассматривается три проецирующих плоскости (см. рис.12):

1. Горизонтально проецирующая плоскость - ^П1. Горизонтальная проекция такой плоскости вырождается в прямую линию (главная проекция). Это главный признак горизонтально проецирующей плоскости на комплексном чертеже. Главная проекция плоскости обладает собирательными свойствами, т.е. проекции всех точек принадлежащих горизонтально проецирующей плоскости на П1 совпадают с главной проекцией этой плоскости.

2. Фронтально проецирующая плоскость -^П2. Фронтальная проекция такой плоскости вырождается в прямую линию (главная прямая). Это признак фронтально проецирующей на комплексном чертеже. Главная проекция (проекция на П2) обладает собирательным свойством, т.е. проекции всех точек, принадлежащих фронтально проецирующей плоскости на П2 совпадают с главной проекцией этой плоскости.

3. Профильно проецирующая плоскость - ^П3. Профильная проекция такой плоскости вырождается в прямую линию (главная проекция). Это признак профильно проецирующей плоскости на комплексном чертеже. Главная проекция обладает собирательным свойством.

Плоскости уровня, т.е. плоскости параллельные какой-либо плоскости проекций, так как плоскости проекций взаимно перпендикулярны, то любая плоскость уровня является одновременно дважды проецирующей. Если плоскость параллельна какой-либо плоскости проекций, то двум другим плоскостям проекций эта же плоскость перпендикулярна. На комплексном чертеже различают три плоскости уровня (см. рис. 12):

1. Плоскость параллельна П1, но перпендикулярна П2 и П3 – горизонтальная плоскость уровня (одновременно такая плоскость является профильно и фронтально проецирующей).

2. Плоскость параллельна П2, но перпендикулярна П1 и П3 – фронтальная плоскость уровня (горизонтально и профильно проецирующая плоскость).

3. Плоскость параллельна П3, но перпендикулярна П1 и П2 – профильная плоскость уровня (горизонтально и фронтально проецирующая плоскость).

Таким образом, каждая плоскость уровня параллельна одной и перпендикулярна двум другим плоскостям проекций, и поэтому плоскости уровня обладают следующими свойствами:

1. Любая линия или плоская фигура, лежащая в плоскости уровня, проецируется без искажений (в натуральную величину) на ту плоскость проекций, которой параллельна плоскость уровня.

2. На две другие плоскости проекций плоскость уровня проецируется в прямые линии, которые перпендикулярны соответствующим линиям связи и которые обладают собирательными свойствами.

7. Взаимное положение прямой и плоскости, двух плоскостей.

Всего возможны три взаимных расположения прямой и плоскости. Прямая может пересекаться плоскостью, может быть параллельна плоскостью или совпадать с плоскостью.

Если прямая пересекается с плоскостью, значит, она имеет с плоскостью одну (не больше) общую точку.

Если прямая параллельна плоскости, то прямая и плоскость не имеют общих точек.

Если прямая совпадает с плоскостью, значит, она имеет с плоскостью как минимум две общие точки.

Рассмотрим более подробно случай пересечения прямой с плоскостью. Частный случай пересечения прямой с плоскостью – прямая расположена под прямым углом к плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна к двум пересекающимся прямым, принадлежащим этой плоскости.

Исходя из выше сказанного, можно сделать вывод, что если прямая перпендикулярна плоскости, то она перпендикулярна к любой горизонтали и фронтали плоскости.

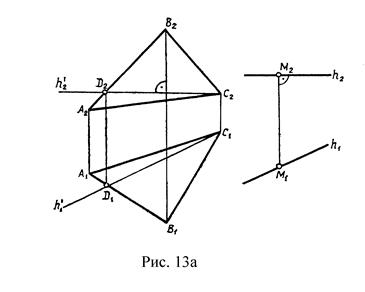
Поскольку прямой угол проецируется на плоскость проекций без искажений, если одна из сторон прямого угла параллельна плоскости проекций, то проекции прямой на перпендикулярной плоскости на комплексном чертеже должны быть следующими: горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали; фронтальная проекция перпендикулярна фронтальной проекции фронтали (рис.13).

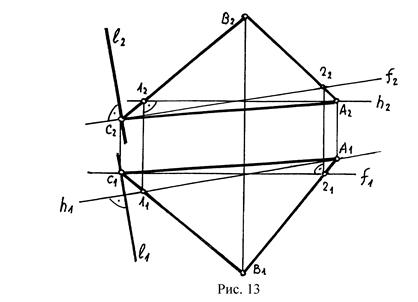
Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (рис.13а).

Из стереометрии известно, что плоскость q перпендикулярна плоскости Р в двух случаях:

1. Если она проходит через прямую l ^Р.

2. Если она проходит перпендикулярно к прямой а, принадлежащей плоскости Р (рис.13б).

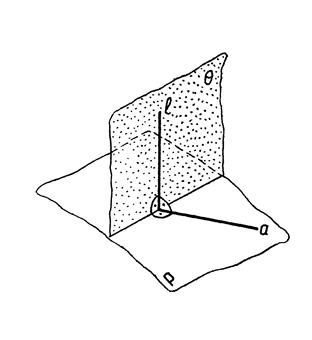
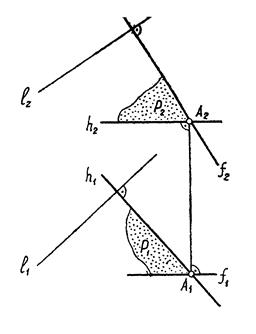
Рис. 13б

Из стереометрии известно и то, что плоскости параллельны между собой, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Пример. Через т.К провести плоскость Р(l Ç m), параллельно плоскости q(l` Ç m`) (рис.13в).

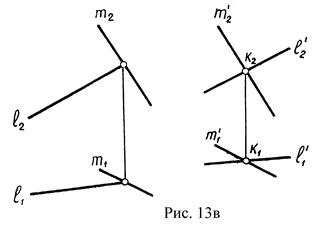
8. Позиционные задачи.

Позиционные задачи – задачи на взаимное пересечение геометрических образов:

1. Пересечение линии и поверхности (плоскости) РÇq=К – точка.

2. Пересечение двух поверхностей (плоскостей) РÇq= l – линия.

При решении задач возможны следующие случаи:

1. Оба геометрических образа являются проецирующими.

2. Один – проецирующий, другой – общего положения.

3. Оба – общего положения.

Рассмотрим первую позиционную задачу: пересечение линии и плоскости.

Искомый элемент – точка. l ÇР=К

Случай 1: Прямая и плоскость являются проецирующими.

В этом случае проекции точки пересечения уже есть на комплексном чертеже. Дополнительные построения для решения такой задачи не нужны (рис.14). Нужен анализ, опирающийся на собирательные свойства проекции образа.

Случай 2: Один геометрический образ проецирующий, а другой общего положения. Решается по схеме:

1. При анализе чертежа должны быть сформулированы собирательные свойства проецирующего геометрического образа.

2. Одна проекция общего элемента (т.е. решение задачи) совпадает с главной (вырожденной) проекцией проецирующего образа. Необходимо выделить и обозначить эту проекцию.

3. Вторая проекция общего элемента находится по условию принадлежности к образу общего положения.

4. Определить взаимную видимость образов.

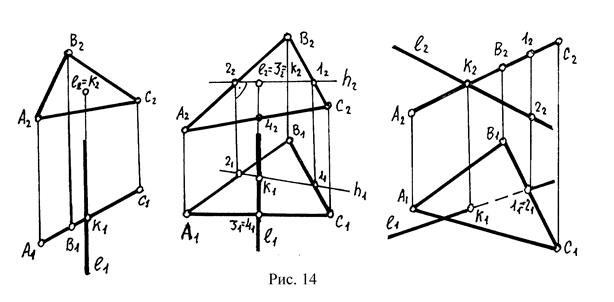
Случай 3: Когда пересекаются прямая и плоскость общего положения, готового решения нет ни на одной из плоскостей проекции. Поэтому для решения подобной задачи требуется вводить плоскость посредник.

Схема решения позиционной задачи №1 (Случай 3).

1. Прямая заключается во вспомогательную проецирующую плоскость (посредник).

2. Плоскость посредник пересекается с заданной плоскостью по прямой линии, ограничив которую двумя точками, несложно построить недостающую проекцию этой прямой линии.

3. Определяется точка пересечения двух линий (т.е. линии пересечения заданной плоскости с плоскостью посредником и заданной прямой). Эта точка и является искомой.

4. Последним пунктом определяется видимость заданной прямой относительно заданной плоскости.

Видимость определяется при помощи конкурирующих точек и без ее определения задача является нерешенной (рис.15).

Рассмотрим вторую позиционную задачу: построение линии пересечения двух плоскостей.

При пересечении двух плоскостей, также как и при пересечении прямой и плоскости, возможны следующие случаи:

РÇq= l

1. Обе плоскости проецирующие.

2. Одна плоскость проецирующая, другая общего положения.

3. Обе плоскости общего положения.

Случай 1: При пересечении плоскостей получается прямая линия. Проекции этой прямой совпадают с проекциями проецирующих плоскостей на основании их собирательных свойств. Проекции такой прямой уже имеются на комплексном чертеже и, следовательно, на требуется никаких дополнительных построений (рис.16).

Случай 2: Пересекаются плоскость общего положения с проецирующей плоскостью, то, как уже говорилось раньше такие задачи решаются по следующей схеме:

1. Формулируются собирательные свойства проецирующей плоскости.

2. Одна проекция линии пересечения совпадает с главной проекцией проецирующей плоскости.

3. Недостающая проекция линии пересечения строится из условия принадлежности к плоскости общего положения.

4. Определяется взаимная видимость (рис.17).

Случай 3: При построении линии пересечения двух плоскостей общего положения необходимо вводить вспомогательные плоскости (посредники). Так как в результате пересечения получается прямая линия, а прямая линия определяется в пространстве двумя точками, то и посредников требуется не меньше двух.

Рассмотрим построение линии пересечения двух плоскостей общего положения на примере.

Плоскость Р задана двумя пересекающимися прямыми, а и b, плоскость Q – двумя параллельными прямыми, e и d. Требуется построить линию пересечения плоскостей Р и Q.

Схема решения позиционной задачи №2 (случай 3):

1. Пересечем данные плоскости Р и Q вспомогательной горизонтальной плоскостью уровня l (l2).

2. Построим линии пересечении плоскости l с заданными плоскостями: lÇР= l (А, В), lÇQ=n(C, D).

3. Найдем точку пересечения построенных прямых l Çn=k. Точка K принадлежит одновременно обеим заданным плоскостям и Р, и Q, следовательно, точка K принадлежит линии пересечения заданных плоскостей.

4. Вводится вторая вспомогательная горизонтальная плоскость уровня D (D2). При помощи плоскости D находится вторая точка F, которая принадлежит линии пересечения.

5. Прямая m линия пересечения плоскостей P и Q проходит через точки K и F (рис.18).

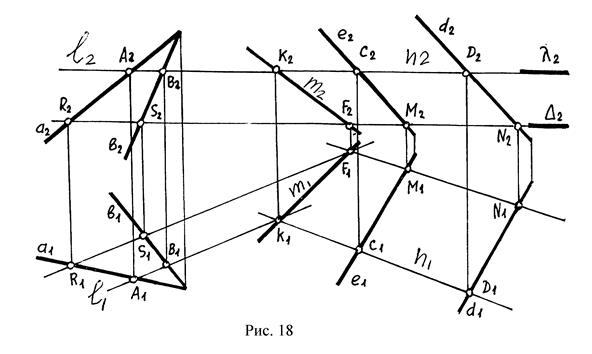
В качестве вспомогательных секущих плоскостей (посредников) можно выбирать любые проецирующие плоскости.

9. Способы преобразования чертежа. Основные задачи преобразования.

Задачи, в которых требуется определить метрические величины углов, длин, площадей, называются метрическими задачами. Решение таких задач значительно упрощается, если заданные на исходном чертеже геометрические образы занимают частные положения (т.е. параллельны или перпендикулярны одной из плоскостей проекций).

В случае, когда геометрические образы расположены в общем положении, возникает необходимость преобразования комплексного чертежа. Цель преобразования – придать геометрическим образам такое частное положение, которое позволяет упростить решение поставленной задачи.

Наиболее часто применяется при решении задач два способа преобразования комплексного чертежа: замена плоскостей проекций и плоскопараллельное перемещение.

При изучении способа плоскопараллельного перемещения важно уяснить следующие основные положения:

1. Плоскости проекций неподвижны, а оригинал перемещается в пространстве;

2. Все точки оригинала перемещаются во взаимно параллельных плоскостях уровня (каждая в своей плоскости).

Если рассматривать плоскопараллельное перемещение прямой или плоскости, то важно учитывать, что в процессе перемещения геометрического образа не изменяется угол его наклона к той плоскости проекций, относительно которой совершается его плоскопараллельное перемещение.

Из выше сказанного следуют основные правила построения комплексного чертежа:

1. Проекция оригинала на плоскости, параллельно которой совершается его движение, сохраняет свою форму и величину, изменяя только положение.

Проекции точек оригинала на другой плоскости проекций перемещаются по прямым, перпендикулярным соответствующим линиям связи (при этом проекция оригинала на эту плоскость меняет свое положение и форму).

При изучении способа замены плоскостей проекций важно понять, что при этом способе оригинал остается неподвижен, а одна из плоскостей проекций заменяется на новую, перпендикулярную к незаменяемой плоскости проекций и расположенную частным образом относительно оригинала. При замене одной из плоскостей новой плоскостью расстояние от точек геометрического объекта до незаменяемой плоскости проекций остаются постоянными. Следовательно, на комплексном чертеже присутствие осей между двумя заданными плоскостями проекций, а также между вновь введенной плоскостью и той, которая осталась обязательной.

Для того чтобы понять, как осуществляется построение на комплексном чертеже при замене плоскостей проекций по отношению к объекту, нужно понять, как происходит замена плоскостей проекций по отношению к точке. Пусть дана точка А (А1,А2) в заданной системе плоскостей проекций П1/П2 (рис.19). Первоначально заменим плоскость П2 на новую плоскость П4 (П4^П1). Помня о том, что линии связи всегда перпендикулярны координатным осям проводим А1А4^X14. Для построения точки А в П4

замеряем расстояние её до незаменяемой плоскости проекций П1, которое снимаем на П2 (от А2 до X12). Затем заменяем плоскость П1 на П5 (П5^П4), П4 в данной замене выполняет роль неподвижной (незаменяемой) плоскости. Плоскости П4 и П5 разделяет ось X45. Для построения точки А в П5 проводим аналогичные рассуждения, что и для построения точки в П4, расстояние точки А до незаменяемой плоскости проекций П4 замеряется на П1 и равно расстоянию от А1 до X14.

Изучив и запомнив основы способов замены плоскостей проекций и плоскопараллельного перемещения, следует научиться решать этим способом основные задачи преобразования комплексного чертежа (табл.2 и 3).

Для способов преобразования комплексного чертежа характерны следующие преобразования в отношении геометрических объектов:

1. Прямая общего положения может быть преобразована в линию уровня.

2. Линия уровня преобразуется в проецирующую прямую.

3. Плоскость общего положения сначала преобразуется в проецирующую плоскость.

4. Проецирующая плоскость может быть преобразована в плоскость уровня.

Способы преобразования комплексного чертежа применяются при решении следующих задач:

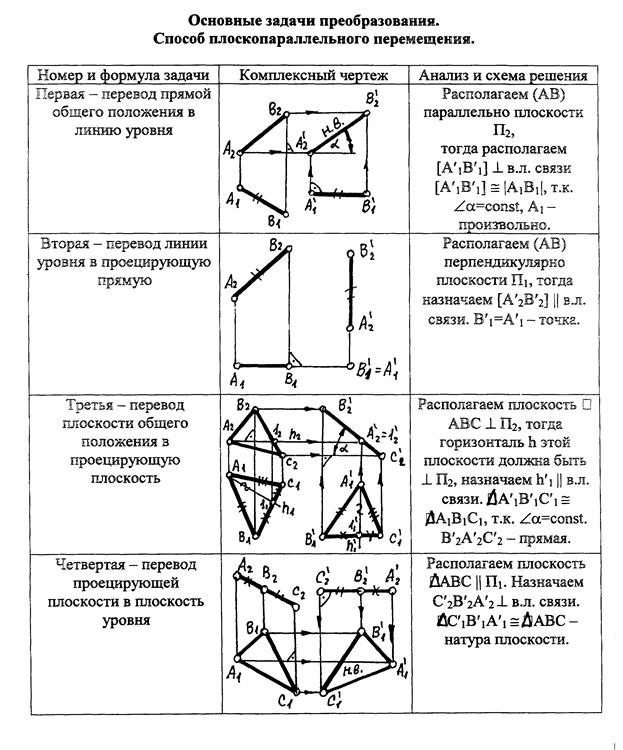
1. Первая задача – перевод прямой общего положения в прямую уровня. Такая задача решается с целью определения натуральной величины отрезка прямой линии и углов её наклона к плоскости проекций.

2. Вторая задача – перевод прямой уровня в проецирующую прямую. Цель решения задачи заключается в определении натуральных величин расстояний от точки до прямой, между параллельными прямыми, между скрещивающимися прямыми; определение натуральной величины двугранного угла (угла между плоскостями).

3. Третья задача – перевод плоскости общего положения в проецирующую плоскость. Область применения задачи – определение натуральной величины углов наклона плоскости к плоскостям проекций, упрощение определения расстояния от точки до плоскости между параллельными плоскостями, упрощение решения задач на взаимное пересечение линии и плоскости, а также плоскости и двух поверхностей.

4. Четвертая задача – перевод проецирующей плоскости в плоскость уровня. Решение необходимо для определения истинного вида плоской фигуры, определение её метрических размеров, выполнение различных геометрических построений в плоскости фигуры.

Таблица 2.

Научившись решать четыре основные задачи преобразования комплексного чертежа, можно приступить к решению любых метрических задач начертательной геометрии. Все метрические задачи можно разделить на три основные группы: определение расстояний, определение углов, определение натурального вида плоских фигур и разверток поверхностей.

Эти задачи имеют широкое распространение при решении практических задач, при проектировании изготовления деталей и сборочных машин и механизмов.

Таблица 3.

10. Кривые линии и их проекционные свойства

10.1. Общие сведения о кривых

Кривая – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в начертательной геометрии рассматривается как траектория, описанная движущейся точкой, как проекция другой кривой, как линия пересечения двух поверхностей и т.д.

Кривая называется плоской, если все ее точки принадлежат некоторой плоскости, в противном случае она называется пространственной. Примером плоской кривой может служить окружность, так как все ее точки размещаются в одной плоскости. Пример пространственной кривой - винтовая линия (рис. 20). К кривым второго порядка относятся: окружность, эллипс, парабола, гипербола. Это все плоские кривые. Если кривая 2-го порядка пересекается с прямой линией или плоскостью, то она не может давать более 2-х точек пересечения. Это ее отличительный признак, выраженный на языке начертательной геометрии. Кривая линия моделируется на плоскость проекций парой кривых.

Проверить плоская это кривая или пространственная можно с помощью 3-х точек А, В, С. Проекции точек должны лежать на проекциях кривой и располагаться на одной линии связи, или необходимо соединить попарно двумя прямыми линиями 4 произвольные точки этой кривой (рис. 21). Если эти прямые окажутся пересекающимися, то заданная на комплексном чертеже кривая – плоская, если скрещивающимися - пространственная. К пространственным кривым относятся все кривые, полученные при пересечении кривых поверхностей.

Кривые линии подразделяются на алгебраические, которые можно задать алгебраическими уравнениями (окружность, эллипс, парабола, гипербола др.) и трансцендентные, уравнение которых имеет вид трансцендентных функций (синусоида, спираль Архимеда и др.).

Важно уметь у алгебраических кривых определить порядок кривой – степень ее уравнения. Порядок плоской кривой геометрически определяется как максимально возможное число точек пересечения кривой с прямой линией, порядок алгебраической пространственной кривой – как максимальное число точек пересечения кривой с плоскостью. Например, прямая линия может пересекаться с эллипсом не более чем в 2-х точках. Отсюда эллипс – кривая второго порядка и его уравнение второй степени.

10.2. Особые точки кривых

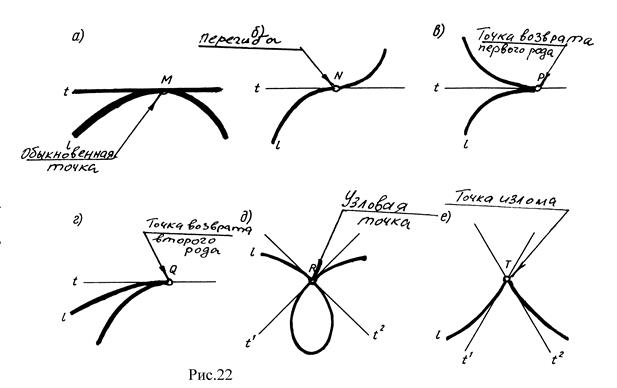
Точки кривых разделяются на обыкновенные (рис.22а) и особые (рис.22б, в, г, д, е). На рис. 22б точка N – точка перегиба, на рис. 22в точка Р – точка возврата первого рода, на рис. 22г точка Q – точка возврата 2-го рода, на рис. 22д точка R – узловая точка, на рис. 22е точка Т – точка излома.

Для характеристики точек плоской кривой необходимо наличие одной проекции кривой, а чтобы судить о характере точек пространственной кривой необходимо наличие двух проекций этой кривой.

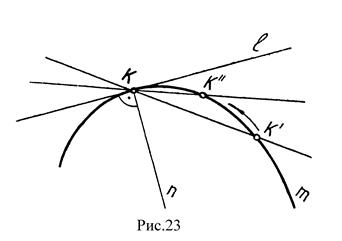
10.3. Секущая, касательная, нормаль к кривой

Прямая, пересекающая кривую в одной, двух и более точек называется секущей (рис. 23 – КК^/). Касательной прямой ℓ к кривой m, в некоторой точке К является предельное положение секущей КК^/, при котором точка К^/ стремится к точке К. Прямая n проведенная через точку К перпендикулярно к касательной ℓ называется нормалью (рис.23). Причем, если прямая касается кривой в пространстве в некоторой точке К, то проекции этой прямой касаются проекций кривой в точках, которые являются проекциями точки касания (рис.21). На практике при анализе плоских кривых необходимо уметь строить касательную из точки, лежащей вне кривой, и через точку, взятую на кривой линии.

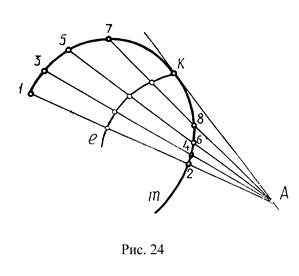
Для построения касательной, проведенной из точки вне кривой (рис.24), проведем из точки А пучок секущих, пересекающих данную кривую m в точках 1,2,3,4….Через середины полученных хорд проводим кривую ошибок ℓ, которая пересекаясь с данной кривой m, определяет точку касания К. Через данную точку касания К и данную точку А проводим искомую касательную.

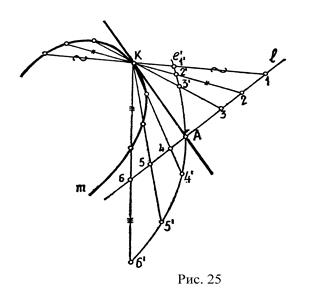
Чтобы построить касательную через точку К, взятую на кривой m, необходимо провести вспомогательную прямую ℓ расположенную приблизительно перпендикулярно к будущей касательной (рис.25). Затем через точку касания К проводим пучок секущих, пересекающих вспомогательную прямую ℓ в точках 1,2,3,4…. От этих точек откладываем соответствующие хорды. Через полученные на секущих точки: 1^/, 2^/, 3^/,… проводим кривую ошибок ℓ^/, которая пересекаясь со вспомогательной кривой ℓ, определяет вторую точку А, искомой касательной.

10.4. Определение длины отрезка кривой

Определение длины отрезка кривой находят приближенно. Для этого кривую линию заменяем на ломаную, вписанную в эту кривую с последующим определением натуральной величины каждого звена ломаной линии, тогда длина отрезка кривой линии определяется приближенно и равна сумме натуральных величин звеньев этой ломаной линии. Все отрезки звеньев ломаной линии размещаем параллельно П₂ и на П₂ определяем натуральную величину отрезка кривой линии (рис.26).

10.5. Цилиндрическая винтовая линия

Из пространственных кривых линий широко применяются в технике винтовые линии, которые являются направляющими поверхностей резьб, червяков, шнеков, пружин, сверл, разверток и т.д.

Цилиндрическая винтовая линия – пространственная кривая, полученная движением точки по образующей цилиндра, которая в свою очередь вращается вокруг его оси. На рис.27 показано образование винтовой линии, построение которой вытекает из способа ее образования движением точки по поверхности цилиндра. Для этого шаг винтовой линии, равный 60 мм делим на 4 части, затем каждую часть делим еще на 3 части, всего получается 12 делений. Основание цилиндра (окружность) делим тоже на 12 частей (см. рис.27а). Все остальное построение показано на рисунке 27.

Фронтальная проекция цилиндрической винтовой линии является синусоидой, а горизонтальная проекция - окружностью развертки цилиндрической винтовой линии – прямая линия, наклоненная к горизонтальной прямой под углом α. Угол α – угол наклона винтовой линии и может быть определен из выражения:

(1)

10.6. Коническая винтовая линия

Конической винтовой линией – называется пространственная кривая, полученная равномерным движением точки по образующей конуса, которая равномерно вращается вокруг его оси. Для построения конической винтовой линии необходимо окружность основания конуса и шаг винтовой линии разделить на 12 частей, затем через точки деления основания провести соответствующие образующие конуса. Положение движущейся точки на каждой образующей конуса находим, исходя из того, что ее движение вдоль образующей пропорционально угловому перемещению этой образующей вокруг оси конуса (рис. 28б). Горизонтальная проекция конической винтовой линии - спираль Архимеда, фронтальная проекция – синусоида с затухающей амплитудой. Развертка конической винтовой линии является тоже спиралью Архимеда (рис. 28б).

(2)

где ℓ– образующая конуса;

R - радиус основания.

11. Гранные и кривые поверхности

11.1. Общие сведения о поверхностях и их изображениях на комплексном чертеже. Точка и линия на поверхности

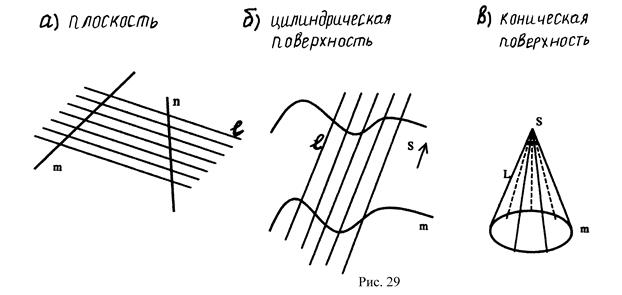
«Поверхность – это след линии, движущейся в пространстве» -это определение поверхности дал древнегреческий математик Эвклид, живший в III-IV веке до н. э. Движущаяся линия называется образующей. Она при своем движении может сохранять или изменять свою форму, подчиняясь какому-либо закону. Закон перемещения образующей включает другие линии, называемые – направляющими, по которым скользит образующая при своем перемещении в пространстве, а также характер движения образующей (рис.29).

В некоторых случаях одна из направляющих может превращаться в точку (рис. 29в) или находиться в бесконечности – цилиндрическая поверхность.

В начертательной геометрии поверхности рассматривают, исходя из кинематики их образования, и поверхность может быть определена как совокупность всех последовательных положений некоторой линии (образующей), перемещающейся в пространстве по определенному закону.

Сочетание образующих и направляющих поверхности называется ее каркасом. На комплексном чертеже любая поверхность задается своим определителем – совокупностью геометрических элементов задающих поверхность, позволяющих реализовать кинематический закон образования поверхности (см. рис. 29) и позволяющих построить каждую точку поверхности.

В зависимости от формы образующей и закона ее перемещения в пространстве, поверхности делят на две группы:

1. Линейчатые поверхности. Образующая – прямая линия.

В свою очередь они подразделяются:

а) на развертываемые б) неразвертываемые

Гранные: Торсовые: С плоскостью Винтовые

Пирамида, конические, параллелизма: поверхности:

призма цилиндри цилиндроид, прямой и

ческие, коноид, косая наклонный

торсовые плоскость геликоид

2. Нелинейчатые поверхности. Образующая – окружность или кривая линия.

Подразделяются:

а) с постоянной образующей: б) с переменной образующей:

1. Поверхности вращения: 1. Циклические (каналовые)

тор, эллипсоид, параболоид, поверхности:

гиперболоид; поверхности труб перемен-

ного сечения;

2. Циклические поверхности: 2. Графические поверхности

трубчатые, пружины (земли, обуви, фюзеляжа

трубы изогнутые самолета).

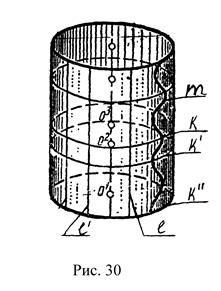
Одна и та же поверхность может быть образована по разному (рис.30). Поверхность цилиндра, например, может быть образована:

1. Вращением образующей ℓ вокруг оси i.

2. Перемещением окружности к вдоль оси i.

3. Вращением вокруг оси i образующей m.

Если направляющей будет ломаная линия, состоящая из ряда прямолинейных звеньев, то поверхность цилиндра превращается в поверхность призмы, а поверхность конуса – в поверхность пирамиды.

11.2. Многогранники. Задание на комплексном чертеже Определение видимости элементов многогранников

Поверхности, состоящие из ряда плоскостей – граней, называются многогранниками. Образуются перемещением образующей по ломаной линии направляющей. Наибольший практический интерес представляют пирамиды и призмы. Элементами многогранников являются вершины, ребра, грани (рис.31).

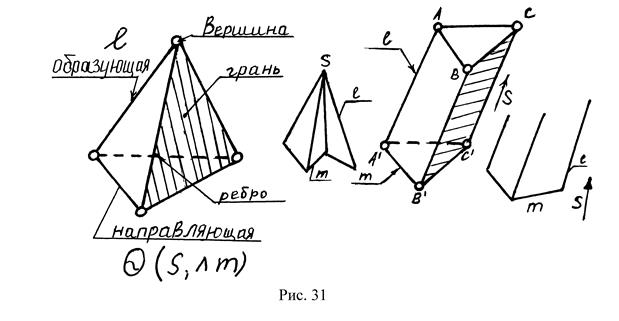
Совокупность всех ребер многогранника называется его сеткой или каркасом. Построение проекций многогранника сводится к построению проекций его сетки (каркаса).

Пирамида образуется перемещением образующей ℓ по ломаной направляющей m, при этом ℓ закреплена в точке S – вершине, которая неподвижна.

Призма образуется перемещением образующей ℓ по ломаной направляющей m, при этом ℓ остается параллельна заданному направлению S.

Задание на комплексном чертеже пирамиды и призмы представлено на рис.32 и рис.33.

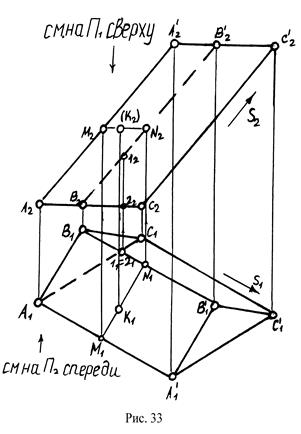
Видимость элементов многогранника определяется с помощью конкурирующих точек (см. рис. 32 и 33) и следующих правил:

1. Линии, образующие внешний контур (очерк) каждой проекции всегда видимы.

2. Если внутри очерка пересекаются проекции двух ребер, то одна из них видимая, а другая – нет. Видимость определяется при помощи конкурирующих точек.

3. Если проекция хотя бы одного из ребер, ограничивающих грань невидима, то невидима вся грань на этой плоскости проекции.

4. Если внутри очерка сходятся в одной точке проекции трех ребер, то или все три видимы, или все три не видны. Исходя из этого, достаточно определить видимость одной из трех проекций ребер, видимость двух других будет такой же.

5. Если видимость на одной проекции определена, видимость на другой проекции можно определить без дополнительных построений. Если последовательность наименований вершин при обходе какой –либо грани по часовой или против часовой стрелки одинакова на обеих проекциях, то и видимость грани на обеих проекциях также одинакова.

11.3. Поверхности вращения

Поверхности вращения имеют широкое применение в технике, так как являются определяющими многих деталей различных механизмов. Это объясняется распространенностью вращательного движения, простотой изготовления и обработки деталей с поверхностями вращения. Образуются вращением производящей линии вокруг неподвижной оси i, перпендикулярной одной из плоскостей проекций. Определителем поверхности вращения является образующая линия ℓ и ось вращения i (см. рис.34). При вращении образующей ℓ вокруг оси i перпендикулярной П₁, т. А и т. Е описывают окружности, плоскости которых перпендикулярны оси i и следовательно параллельных между собой. Они называются параллелями и проецируются без искажения на ту плоскость, которая перпендикулярна оси i.

Параллель наименьшего диаметра называется горлом, наибольшего – экватором. Линия пересечения поверхностей ращения с плоскостью, проходящей через ось i, называется меридианом, а секущая плоскость называется меридиальной. Если секущая плоскость параллельна плоскости проекции П₂, то она называется плоскостью главного меридиана. Эта плоскость определяет очерк поверхности на П₂, разбивает поверхность на две части: переднюю – видимую на П₂ и заднюю – не видимую на П₂, что позволяет определить видимость элементов поверхности вращения при взгляде спереди. Совокупность меридианов или параллелей (или их сочетание) образует каркас поверхности вращения. Каждую точку поверхности можно построить с помощью линий каркаса. Наиболее удобными линиями при этом построении являются параллели.

11.4 Виды поверхностей вращения

Не нашли, что искали? Воспользуйтесь поиском: