Кинетическая энергия системы частиц.

Элементарная работа, которую совершают все силы, действующие на все частицы системы:

,

где - суммарная кинетическая энергия системы. Кинетическая энергия системы – величина аддитивная: она равна сумме кинетических энергий отдельных частей системы независимо от того, взаимодействуют они между собой или нет.

Приращение кинетической энергии системы равно работе, которую совершают все силы, действующие на все частицы системы. При элементарном перемещении всех частиц

(8.41)

а при конечном перемещении

(8.42)

Уравнение (8.41) можно представить и в другой форме, поделив обе части его на соответствующий промежуток времени dt. Имея при этом в виду что, получим

(8.43)

т. е. производная кинетической энергии системы по времени равна суммарной мощности всех сил, действующих на все частицы системы,

Все силы делят на потенциальные и непотенциальные (диссипативные). Потенциальными называют силы, зависящие при данном характере взаимодействия только от конфигурации механической системы. Работа этих сил, как было показано, равна убыли потенциальной энергии системы.

К непотенциальным силам относятся так называемые диссипативные силы - это силы трения и сопротивления, а также энергетические силы, вызывающие увеличение механической энергии системы за счет других видов энергии (например, взрыв артиллерийского снаряда). Важной особенностью данных сил является то, что суммарная работа внутренних диссипативных сил рассматриваемой системы отрицательна, а энергетических сил - положительна, причем в любой системе отсчета.

Любая диссипативная сила может быть представлена в виде

(8.44)

где - скорость данного тела относительно другого тела (или среды), с которым оно взаимодействует; - положительный коэффициент, зависящий в общем случае от скорости. Сила 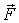всегда направлена противоположно вектору . В зависимости от выбора системы отсчета работа этой силы может быть как положительной, так и отрицательной. Суммарная же работа всех внутренних диссипативных сил - величина всегда отрицательная.

Найдем элементарную работу произвольной пары диссипативных сил взаимодействия между телами 1 и 2 в системе отсчета, где скорости этих тел в данный момент равны :

Теперь учтем, что - скорость тела 1 относительно тела 2, а также то, что . Тогда ,

Или

(8.45)

Разделив силы на внешние и внутренние, а внутренние, в свою очередь,- на потенциальные и непотенциальные, из предыдущего:

Учтем, что работа внутренних потенциальных сил равна убыли собственной потенциальной энергии системы, т.е.

Тогда

(8.46)

Механическую энергию системы представим как сумму кинетической и потенциальной энергии системы:

(8.47)

Энергия Е зависит от скоростей частицы системы, характера взаимодействия между ними и конфигурации системы. Кроме того, энергия Е, как и потенциальная энергия U, определяется с точностью до прибавления несущественной произвольной постоянной и является величиной неаддитивной, т. е. энергия Е системы не равна в общем случае сумме энергий ее отдельных частей. В соответствии c (8. 37)

(8.48)

где - механическая энергия части системы, - потенциальная энергия взаимодействия ее отдельных частей.

Перепишем (8.46) с учетом (8.47) в виде

(8.49)

При конечном изменении

(8.50)

т. е. приращение механической энергии системы равно алгебраической сумме работ всех внешних сил и всех внутренних непотенциальных сил.

Уравнение (8.49) можно представить и в другой форме,

.

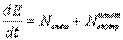(8.51)

т. е. производная механической энергии системы по времени равна алгебраической сумме мощностей всех внешних сил и всех внутренних непотенциальных сил.

Уравнения (8.49) - (8.51) справедливы как в инерциальной, так и в неинерциальной системах отсчета. Следует только иметь в виду, что в неинерциальной системе отсчета необходимо учитывать работу (мощность) и сил инерции, играющих роль внешних сил, т. е. под надо понимать алгебраическую сумму работ внешних сил взаимодействия и работу сил инерции . Чтобы выделения этого обстоятельства, запишем уравнение (8.50) в виде

(8.52)

Итак, закон сохранения механической энергии: в инерциальной системе отсчета механическая энергия замкнутой системы частиц, в которой нет непотенциальных сил, сохраняется в процессе движения, т. е.

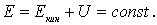
(8.53)

Такую систему называют консервативной. С достаточно хорошим приближением замкнутой консервативной системой можно считать Солнечную систему.

При движении замкнутой консервативной системы сохраняется именно полная механическая энергия, кинетическая же и потенциальная в общем случае изменяются. Однако эти изменения происходят всегда так, что приращение одной из них в точности равно убыли другой, т. е. Это справедливо только в инерциальных системах отсчета.

Если замкнутая система неконсервативная, т. е. в ней имеются непотенциальные силы, то механическая энергия такой системы, согласно (8.45), изменяется, а в случае диссипативных сил убывает:

(8.54)

Универсальный закон сохранения энергии: энергия никогда не создается и не уничтожается, она может только переходить из одной формы в другую или обмениваться между отдельными частями материи.

Согласно (8.54), можно сказать: при уменьшении механической энергии замкнутой системы всегда возникает эквивалентное количество энергии других видов, не связанных с видимым движением. В этом смысле уравнения (8.49) - (8.51) можно рассматривать как более общую формулировку закона сохранения энергии, в которой указана причина изменения механической энергии у незамкнутой системы.

В частности, механическая энергия может сохраняться у незамкнутых систем, но это происходит лишь в тех случаях, когда, согласно уравнению (8.50), уменьшение этой энергии за счет работы против внутренних диссипативных сил компенсируется поступлением энергии за счет работы внешних сил.

В заключение отметим, что при решении большинства задач закон сохранения энергии применяют обычно совместно с законом сохранения или импульса, или момента импульса, или с тем и другим одновременно.

Не нашли, что искали? Воспользуйтесь поиском: