
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Кинетическая энергия тела при плоском движении.
Плоское движение тела, может быть представлено как наложение двух движений — поступательного с некоторой скоростью v0 и вращения вокруг соответствующей оси.. Свяжем с телом систему координат К ', ось z ' которой направим вдоль вектора угловой скорости вращения тела w. Тогда скорость элементарной массы тела в неподвижной системе координат К может быть представлена в виде
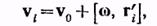
где уо — скорость начала координат О' системы К.', т'{ — радиус-вектор, определяющий положение элементарной массы по отношению к точке О'.
Кинетическая энергия i-и элементарной массы равна

Или

Векторное произведение 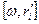 можно, как мы знаем из кинематики, заменить векторным произведением
можно, как мы знаем из кинематики, заменить векторным произведением 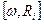 , где Ri- перпендикулярная к оси z' составляющая радиуса-вектора
, где Ri- перпендикулярная к оси z' составляющая радиуса-вектора
Модуль этого векторного произведения равен wRi (векторы - взаимно перпендикулярны). Следовательно, получим кинетическую энергию тела в виде:
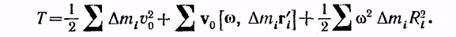
Или
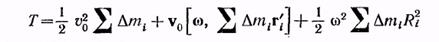
Или
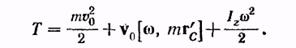
Это выражение можно упростить, взяв в качестве точки О' центр инерции тела С, т. е. поместив начало системы координат К.' в точку С. В этом случае r 'с = 0,
так что второе слагаемое исчезает. Поэтому, обозначив через vc скорость центра инерции, а через Iс — момент инерции тела относительно оси вращения, проходящей через точку С, получим для кинетической энергии тела формулу:
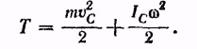
Таким образом, кинетическая энергия тела при плоском движении слагается из.энергии поступательного движения со скоростью, равной скорости центра инерции, и энергии вращения вокруг оси, проходящей через центр инерции тела.
Использование графиков потенциальной энергии для качественного анализа поведения частицы.
Потенциальная яма.
Не нашли, что искали? Воспользуйтесь поиском: