Проектування точки.

Найбільш простим і зручним є проектування на взаємно перпендикулярні площини проекцій за допомогою проектуючих променів, що перпендикулярні площинам проекцій. Таке проектування називається ортогональним проектуванням, а отриманні зображення – ортогональними проекціями.

Рис. 2. Розташування площин проекцій.

Площина Н – горизонтальна площина проекцій, площина V – фронтальна площина проекцій, площина W – профільна площина проекцій. Лінії перетину площин проекцій називаються осями проекцій, або осями координат і позначаються Ox, Oy, Oz.

Кут, утворений трьома площинами проекцій, називають координатним кутом.

Зображення, отримані на площинах координатного кута і суміщені в одну площину, називають епюром або ортогональним кресленням. Розглянемо побудову епюра точки.

Існує декілька способів отримання комплексного креслення точки:

1) за заданими координатами (рис. 3, а);

2) за допомогою циркуля (рис. 3, б);

3) за допомогою прямої, проведеної під кутом 45⁰ до осі Y (рис. 3, в);

4) за допомогою бісектриси в четвертій чверті (рис. 3, г).

Рис. 3. Способи отримання комплексного креслення точки.

5. Класифікація прямих.

В залежності від розташування прямої відносно площин проекцій виділяють загальне і окреме її положення.

Пряма загального положення – довільна пряма, що не паралельна і не перпендикулярна жодній з площин проекцій (рис. 4).

Прямі окремого положення поділяються на прямі рівня (горизонтальна, фронтальна та профільна) та проектуючі прямі (горизонтально-проектуюча, фронтально-проектуюча, профільно-проектуюча).

Горизонтальна пряма – пряма, паралельна площині Н (рис. 5).

Фронтальна пряма – пряма паралельна площині V (рис. 6).

Профільна пряма – пряма паралельна площині W (рис. 7).

Рис. 4. Пряма загального положення.

Рис. 5. Горизонтальна пряма.

Рис. 6. Фронтальна пряма.

Рис. 7. Профільна пряма.

Прямі, перпендикулярні одній з площин проекцій, називають проектуючими прямими.

Горизонтально-проектуюча пряма перпендикулярна площині Н (рис. 8). Фронтально-проектуюча пряма – пряма перпендикулярна площині V (рис. 9). Профільно-проектуюча пряма – пряма перпендикулярна площині W (рис. 10).

Рис. 8. Горизонтально-проектуюча пряма.

Рис. 9. Фронтально-проектуюча пряма.

Рис. 10. Профільно-проектуюча пряма.

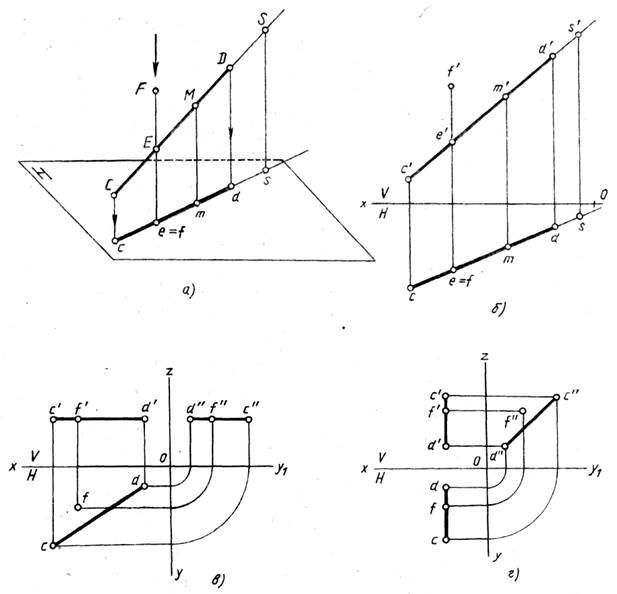
Рис. 11. Належність точки прямій.

6. Належність точки прямій.

Якщо точка належить прямій, то її проекції лежать на однойменних проекціях цієї прямої і на одній лінії проекційного зв’язку (рис. 11, а, б).

Точка не належить прямій лінії, якщо хоча б одна її проекція не належить відповідній проекції прямої (рис. 11, в, г).

7. Сліди прямої.

Сліди прямої – це точки перетину прямої з площинами проекцій.

Побудова слідів прямої загального положення зображена на рис. 12.

Рис. 12. Сліди прямої.

Побудова горизонтального сліду (К^ІL^І):

1. А^ІІВ^ІІ продовжуємо до перетину з віссю Х₁₂ (А^ІІL^ІІ);

2. З т. L^ІІ в площині проекцій П₁ проводимо вертикальну лінію до перетину з продовженням А^ІВ^І (т. L^І);

3. З т. L^І через А^ІВ^І проводимо пряму К^ІL^І – горизонтальний слід.

Аналогічно виконується побудова фронтального сліду.

8. Натуральна величина відрізка.

Натуральна величина відрізка прямої АВ – це гіпотенуза прямокутного трикутника, одним катетом якого є одна з проекцій, а другим – різниця відстаней кінців відрізка на другій проекції до відповідної площини проекцій.

Приклад визначення натуральної величини відрізка показано на рис. 13.

9. Відносне положення прямих.

Прямі перетинаються, якщо точки перетину відповідних прямих лежать на одній вертикальній лінії зв’язку (рис. 14, а).

Прямі паралельні, якщо паралельні їх однойменні проекції (рис. 16).

Прямі мимобіжні, якщо точки перетину їх однойменних проекцій не лежать на одній вертикальній лінії зв’язку (рис. 14, б; 15; 17; 18; 19).

Рис. 13. Натуральна величина відрізка прямої.

Рис. 14. Прямі, що перетинаються (а) та мимобіжні прямі (б).

б)

Рис. 15. Мимобіжні прямі.

Рис. 16. Паралельні прямі.

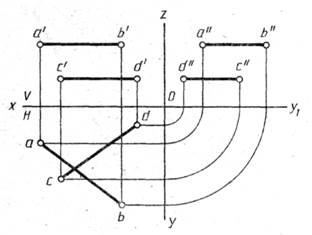
Рис. 17. Мимобіжні прямі. Рис. 18. Мимобіжні прямі.

Рис. 19. Мимобіжні прямі.

Питання для самоконтролю:

1. У чому полягає відмінність центрального і паралельного видів проектування?

2. За відомими проекціями А^ІІ і А^ІІІ знайдіть проекцію А^І трьома методами.

3. Які положення може займати пряма лінія?

4. Умова належності точки до прямої.

5. Що таке горизонтальний слід і як він будується?

6. Що таке фронтальний слід і як він будується?

7. Як визначається натуральна величина відрізка?

8. Які існують відносні положення двох прямих ліній?

Лекція 2. Проектування площин.

План.

1. Способи зображення площини на кресленні.

2. Класифікація площин.

3. Належність прямих і точок до площини.

4. Головні лінії площини.

5. Взаємний перетин площин.

1. Способи зображення площини на кресленні.

Положення площини в просторі визначається трьома її точками, що не лежать на одній прямій. Тому, щоб задати на епюрі площину, достатньо задати три її точки (рис. 1).

Площину можна задати точкою і прямою (рис. 2, а), двома паралельними прямими (рис. 2, б), двома прямими, що перетинаються (рис. 2, в), трикутником (рис. 2, г). Можна задати площину слідами.

Рис. 1. Зображення площини на кресленні.

Рис. 2. Способи зображення площини.

Слідом площини називають пряму, по якій дана площина перетинає площину проекцій. На рис. 3 P_V – фронтальний слід площини P, P_H – горизонтальний слід площини P, P_W – профільний слід площини P.

Рис. 3. Слід площини загального положення.

2. Класифікація площин.

Площина загального положення – це площина, розташована під нахилом до всіх площин проекцій (рис. 3). Така площина перетинається з трьома площинами проекцій по прямих, які є слідами цієї площини. Кожна пара слідів сходиться в точці, яка є точкою сходу слідів площини і розташовується на осі проекцій. Площина загального положення має три точки сходу, які позначаються P_x, P_y, P_z . В цих точках площина перетинає осі координат. Плоскі фігури, що лежать в площині загального положення, проектуються на площини проекцій із спотворенням.

Проектуюча площина – це площина, що перпендикулярна якій-небудь площині проекцій.

Горизонтально-проектуюча площина – це площина, що перпендикулярна горизонтальній площині проекцій H (рис. 4).

Фронтально-проектуюча площина – це площина, що перпендикулярна фронтальній площині проекцій V (рис. 5).

Профільно-проектуюча площина – це площина, що перпендикулярна профільній площині проекцій W (рис. 6).

Проектуюча площина проектується на площину проекцій, до якої вона перпендикулярна, в пряму.

Рис. 4. Горизонтально-проектуюча площина.

Рис. 5. Фронтально-проектуюча площина.

Рис. 6. Профільно-проектуюча площина.

Площини, перпендикулярні двом площинам проекцій, паралельні третій площині проекцій. Геометричні фігури, що лежать в цих площинах, проектуються без спотворення на ту площину проекцій, якій паралельна дана площина (рис. 7, 8, 9). Називаються такі площини так само, як і площина проекцій, паралельно якій вони розташовані: горизонтальна площина (рис. 7), фронтальна площина (рис. 8), профільна площина (рис. 9).

Рис. 7. Горизонтальна площина.

Рис. 8. Фронтальна площина.

Рис. 9. Профільна площина.

3. Належність прямих і точок до площини.

Пряма може лежати в площині, перетинатися з нею або бути паралельною площині. Пряма лежить у площині, якщо дві її точки належать площині (рис. 10, а).

Перетин прямої з площиною вважається першою основною позиційною задачею нарисної геометрії (рис. 10, б).

Алгоритм визначення точки перетину прямої з площиною складається з чотирьох операцій:

1) через пряму проводять проектуючу площину;

2) знаходять лінію перетину заданої площини з проектуючою;

3) визначають точку перетину двох прямих – заданої та лінії перетину;

4) видимість відрізків прямої визначається за допомогою конкуруючих точок.

Якщо пряма паралельна площині, то відрізок прямої повинен бути паралельний якійсь прямій площини (рис. 10, в).

Точка може належати площині або не належати їй, це визначається за допомогою прямої, що лежить у площині (рис. 11).

4. Головні лінії площини.

До прямих, що займають особливе положення в площині, відносять горизонталі, фронталі, профільні прямі та лінії найбільшого нахилу до площин проекцій.

Ці лінії називають головними лініями площини.

Рис. 12. Головні лінії площини.

Горизонталь – це пряма, що лежить в площині і паралельна горизонтальній площині проекцій H (рис. 12).

Фронталь – це пряма, що належить площині і паралельна фронтальній площині проекцій V (рис. 12).

З трьох ліній найбільшого нахилу до площин проекцій виділяють лінію найбільшого нахилу до горизонтальної площини проекцій H. Цю лінію називають лінією ухилу.

Лінія ухилу – це пряма, що лежить в площині і перпендикулярна її горизонталям (рис. 13).

Рис. 13. Лінія ухилу.

5. Взаємний перетин площин.

Дві площини завжди між собою перетинаються, а коли лінія перетину є нескінченно віддаленою прямою, – площини паралельні.

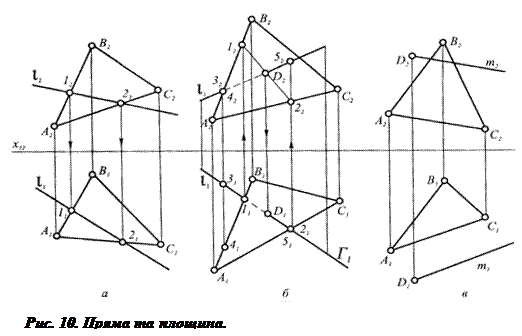
Для визначення лінії перетину площин – другої основної позиційної задачі – треба знайти дві її точки (рис. 14). Це можна зробити, повторивши двічі задачу на перетин прямої з площиною.

Алгоритм визначення прямої перетину двох площин складається з таких операцій:

1) через пряму m проводять фронтально-проектуючу площину Λ;

2) знаходять лінію перетину 1-2 площини Λ з DАВС;

3) визначити проекцію точки D, що лежить на перетині 1-2 з прямою m;

4) проекції точки Е знаходяться аналогічно за допомогою фронтально-проектуючої площини Г.

5) пряма ЕD буде лінією перетину двох площин.

Рис. 14. Перетин площин.

Питання для самоконтролю:

1. У чому полягає відмінність між горизонтальною і фронтально-проектуючою площинами?

2. У чому полягає відмінність між фронтальною і горизонтально-проектуючою площинами?

3. За якої умови вважається, що пряма лежить у площині?

4. Сформулюйте першу основну позиційну задачу нарисної геометрії.

5. З якою метою в креслення вводяться конкуруючі точки?

6. За якої умови вважається, що пряма паралельна площині?

7. За якої умови дві площини, які перетинаються між собою можна вважати паралельними?

8. Сформулюйте другу основну позиційну задачу нарисної геометрії.

Лекція 3. Перетворення комплексного креслення.

План.

1. Метод заміни площин проекцій.
2. Перетворення площин загального положення в площину рівня.
3. Аксонометричні проекції.

1. Метод заміни площин проекцій.

Метричні та позиційні характеристики геометричних образів легко визначити при їх окремому положенні відносно площин проекцій. Оскільки на практиці геометричні образи найчастіше знаходяться в загальному положенні, треба їх привести із загального положення в окреме.

Метричні задачі зводяться до розв'язання чотирьох основних задач:

1) перетворення прямої загального положення в пряму рівня;

2) перетворення прямої загального положення в проектуючу;

Не нашли, что искали? Воспользуйтесь поиском: