ПО РАЗДЕЛУ МАТЕМАТИКИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВЕТЕРИНАРНОЙ МЕДИЦИНЫ И БИОТЕХНОЛОГИИ ИМ. К.И. СКРЯБИНА»

_______________________________________________________________

Джугели Т.П., Кишкинова О.А., Кутликова И.В., Федькина Т.В.

Методические указания для решения контрольной работы

ПО РАЗДЕЛУ МАТЕМАТИКИ

«ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ»

Москва 2011

УДК

Джугели, Т.П., Кишкинова, О.А., Кутликова, И.В., Федькина, Т.В.

Дифференциальные уравнения: учеб.-метод. указ. / Т.П. Джугели, О.А. Кишкинова, И.В. Кутликова, Т.В. Федькина. – М.: ФГОУ ВПО МГАВМиБ им. К.И. Скрябина, 2011. – 24 с.

В методических указаниях приведены необходимые теоретические сведения и формулы, даны решения типовых задач, приведены задачи для самостоятельного решения контрольной работы по разделу математики «Дифференциальные уравнения».

Рекомендованы для студентов обучающихся по специальностям:

020400 бакалавр «Биологии», 240700 бакалавр «Биотехнологии»,

111900.62 бакалавр «Ветсанэкспертизы», 260200 бакалавр «Продуктов питания животного происхождения», 260100 бакалавр «Продуктов питания из растительного сырья», 100800 «Товароведение» (очная и заочная форма обучения), 111100 бакалавр «Зоотехнии» (очная и заочная форма обучения).

Рецензенты: Белановский А.С., канд. техн. наук, профессор (ФГБОУ ВПО МГАВМиБ).

Утверждено на заседании учебно - методической комиссии

ветеринарно – биологического факультета ФГБОУ ВПО МГАВМиБ

(протокол № от 23 января 2012 г.)

Примерные варианты

контрольной работы по математике

с подробным решением для студентов

I курса ВБФ

по теме: «Дифференциальные уравнения».

Вариант I

1.Решить задачу Коши при начальных условиях , 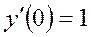для дифференциального уравнения

Для нахождения частного решения необходимо найти общее решение дифференциального уравнения. Составим характеристическое уравнение: и

найдем его корни:

Таким образом, имеем два равных действительных корня , подставим данное число в соответствующую формулу решения дифференциального уравнения , таким образом, - общее решение данного дифференциального уравнения.

Для нахождения частного решения необходимо найти значения , соответствующие начальным условиям, для чего составим систему:

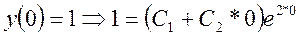
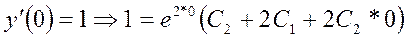, то есть

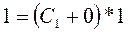
Таким образом, - частное решение данного дифференциального уравнения.

2. Решить уравнение

Так как дифференциальное уравнение I порядка, попытаемся разделить в нем переменные:

Получив уравнение с разделенными переменными, интегрируем его:

Пусть , тогда ; проведем замену для первого интеграла: 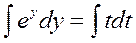; , проводим обратную замену переменной: - интеграл дифференциального уравнения.

Выразим искомую переменную y; для чего прологарифмируем равенство: ; - общее решение дифференциального уравнения.

3. Решить дифуравнение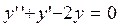

Для нахождения решения составим характеристическое уравнение:

и найдем его корни:

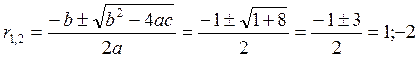
Таким образом имеем два разных действительных корня, которые необходимо подставить в соответствующую формулу решения дифуравнения:

Значит -общее решение дифуравнения.

4. Решить дифуравнение

Составим характеристическое уравнение:

и найдем его корни:

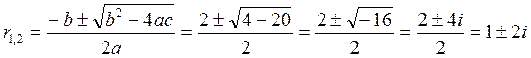
Коэффициенты комплексных корней и подставим в соответствующую формулу решения дифуравнения:

.

Значит, - общее решение дифуравнения.

Вариант II

1. Решить дифференциальное уравнение и найти частное решение при

Для нахождения частного решения необходимо найти общее; попытаемся разделить переменные в данном дифференциальном уравнении I порядка:

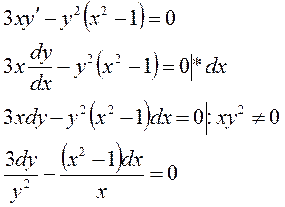
Так как переменные удалось разделить, проинтегрируем равенство:

- интеграл дифференциального уравнения

Выразим искомую величину: - общее решение дифференциального уравнения

Найдем частное решение, используя начальные условия:

Таким образом, - частное решение дифференциального уравнения.

2. Решить уравнение

Составим характеристическое уравнение и решим его:

; получим 2 комплексных корня и коэффициенты комплексных корней: 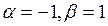. Подставим данные в соответствующую формулу решения дифференциального уравнения:

.

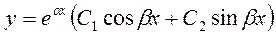Имеем, - общее решение данного дифференциального уравнения.

3. Решить дифуравнение

Для нахождения решения составим характеристическое уравнение:

и найдем его корни:

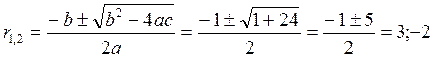
Таким образом имеем два разных действительных корня, которые необходимо подставить в соответствующую формулу решения дифуравнения:

Значит, -общее решение дифуравнения.

4. Решить дифуравнение

Составим характеристическое уравнение:

и найдем его корни:

Таким образом, имеем два равных действительных корня, т.е. ; подставим это значение в соответствующую формулу решения дифуравнения:

.

Значит, 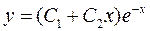- общее решение дифуравнения.

Вариант III

1. Решить задачу Коши для дифференциального уравнения при

Найдем общее решение дифференциального уравнения I порядка; попытаемся разделить переменные:

Получили уравнение с разделенными переменными, далее его следует проинтегрировать: , пусть ,

тогда 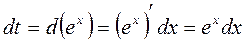; проведём в правом интеграле замену:

- интеграл дифференциального уравнения

Выразим из равенства искомую величину:

- общее решение дифференциального уравнения

Найдем частное решение, используя начальное условие :

Имеем - частное решение дифференциального уравнения.

2. Решить дифуравнение

Для нахождения решения составим характеристическое уравнение:

и найдем его корни:

Таким образом имеем два разных действительных корня, которые необходимо подставить в соответствующую формулу решения дифуравнения:

Значит, 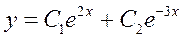-общее решение дифуравнения.

3. Найти частное решение дифуравнения при заданных условиях ,

Для нахождения общего решения дифуравнения составим его характеристическое уравнение и решим его:

Таким образом, имеем два комплексных корня, коэффициенты которого и необходимо подставить в соответствующую формулу решения дифуравнения:

.

Значит, - общее решение дифуравнения.

Для нахождения частного решения по заданным условиям необходимо найти значения и 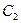; для чего составим систему уравнений, получаемых для соответствующих условий:

;

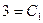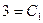
Значит, - искомое частное решение дифуравнения.

4. Решить дифуравнение

Для нахождения решения составим характеристическое уравнение:

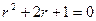и найдем его корни:

Таким образом имеем два равных действительных корня; полученное значение необходимо подставить в соответствующую формулу решения дифуравнения:

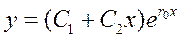
Значит, 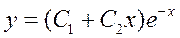-общее решение дифуравнения

Не нашли, что искали? Воспользуйтесь поиском: