Тізбектелген импульстердің перодтарын талдау

Ұзақтығы тізбектелген тікбұрышты импульстер кернеуінің жүру жиілігі және амплетудасы U_m теңдеуін , Фурье қатарына қоямыз (сурет 1,3.а). Егер санау уақтысын импульстің ортасынан жүргізгенде, онда уақыттық функция жұп және Фурье қатарында тұрақтысы болады (сурет1,3.б) және оның косинустық құраушылары: бірінші гармониялық кернеу (сурет 3.в), екінші гармониялық (сурет1,3,г), үшінші гармониялық кернеу (сурет1,3.д) болады:

(1,1)

Содан соң бірінші гармониялық жиілігі, импульстің келесі жиіліктеріне тең болады:

,

мұндағы: жүру жиілігі; – жүру; – жүру электр жиілігі.

Тұрақты құраушы - ді анықтау үшін, бір импульстің ауданын табамыз және оны жүру периоднына бөлеміз:

, (1,2)

мұндағы q – импульстің тереңдік деңгейі.

Сурет1,3.а-г. Импульстердің тікбұрышты тізбектері, (а) және

гармониялық уақыттың диаграмма құраушылары (б), (в), (г)

Бірінші импульстің сигналдық амплитудасын анықтау үшін -ді бірінші теңдеудің барлық қосынды қатарын көбейтеміз және оны бір период аралығының жүруіне интегралдаймыз:

(1,3)

Белгілі болғандай ауданның оң және теріс мәні диаграммалық косинус және синус функциясының барлық жиіліктері өзара тең және сонымен қатар бұл функцияның әрбір интегралы нольге тең болады. Сондай-ақ интегралының көбейтіндісі солай болады, бұл көбейтінді сияқты жәй косинус функциясының суммасына тең:

,

мұндағы R және m – әр түрлі бүтін дұрыс сан.

Қалған бір қосынды мынаған тең болады:

Бұдан:

анықтау үшін (1,1) теңдеу қатарын барлық қосындысын көбейтеміз және оны 0-ден денің интегралдаймыз. Интегралдың 0-ге теңдігі болатын мәндерді ескеріп, ол және -дан аламыз:

Сонымен, екінші гармониялық амплитуда теңдігі:

Сондай-ақ (1) теңдеу қатарын көбейтіп, гармониялық түрге сәйкес амплитуданы анықтаймыз:

n- ді гармониялық үшін:

(1,4)

Бұл жағдайда ол екі кескін аралығының уақыты әрбіреуінікі болғанда, қалған уақытта . Сондықтан n -нің гармониялық амплитудасы тең:

типті функция алу үшін көбейтінді мәнін алымына және бөліміне ендіреміз. Мұндағы :

(1,5)

Енді, барлық гармониялық амплитудаларды біле отырып, диаграмасын тұрғызамыз (3.д-сурет). Координат бастамасына тұрақты құраушы сызығын саламыз .

Сурет 1,3.д. Гармониялық амплитудалардың диаграмасы

Егер гармониялық сан n жоғары емес болса, ондай жағдай импульстің деңгейі жоғары q бұрышы х өте аз болады. Мұны х – ты q арқылы белгілеп көреміз:

(1,6)

Мысалы: егер n=1 және q=1000 бұрыш болғанда. Мұндай кішкентай бұрыш және .

Бұдан бірінші гармониялық амплитуда , тұрақты құраушы -ден екі есе үлкен. Жиілкікке қарсы кескінін саламыз. Жуықша теңдік мағынасы, х-тың аз мәні аймағында синус бұрыштың өзгеруі бұрышқа тура пропорционал болады. Содан соң функция өсуі баяуланады және егер максимум жеткенде, синусты функцияның өзгеріс жылдамдығы нольге тең болады. Сондықтан екінші гармониялық амплитудасы аздау, біріншіне қарағанда, үшінші амплитуда - екіншіден аздау. т.с.с, егер болса, ал болғанда:

.

Егер бұрыш , онда және . Бұл нүкте диаграмма сипатының тек, ол жиілік өсінде орналасқан және келесі мәнге сәйкес келеді жиілігі орналасқан және гармониясы n, теңдеуі:

.

Гармониясы n-нен жоғары q-ге өткенде және болғанда, өсу байқалады және , оның белгісі теріс. Бұл өсім бұрыш кезінде тоқтайды. сәйкес. Онда

Ары қарай n және х өсуі кемуіне байланысты және , онда , иілгіш спектр екінші рет жиілік осімен қиылысады. Сондықтан, мұндағы гармония саны , ал оның жиілігі

Келесі иілу максимумы , 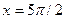кезінде болады, максимум шамасы тең

Егер гармоника саны оның жиілігі және , сондай – ақ Сонымен үшінші аяқталады, иілу тармағы оң болады. Төртінші тармақ аймақтың теріс мәнінде тұрады, жету шамасы онда және аяқталуы және .

Әрбір келесі тармақты бұрынғыдай жиілік аймағы қамтиды және гармония саны q тең.

Не нашли, что искали? Воспользуйтесь поиском: