РЕШЕНИЕ ЗАДАЧ В СЕТЕВОЙ ФОРМЕ

При решении транспортных задач рассматривался случай, когда ис­ходные условия давались в таблице - матрице. Такая запись условий и соответствующие способы решений назывались матричными. Нагляднее изображать условия транспортной задачи на карте или карте-схеме, где зафиксированы пункты расположения поставщиков и потребителей, а также дороги между ними - транспортная сеть. Такая запись представля­ет собой постановку задачи в сетевой форме.

Задача 8.8. Сеть (или линейный граф) состоит из множества узлов (вершин или точек) и множества дуг (ребер или звеньев), соединяющих различные пары узлов. На каждой дуге задана определенная ориентация (определенное направление). Поэтому говорят, что сеть является ориен­тированной.

Для описания ориентированной сети необходимо пронумеровать уз­лы числами натурального ряда 1, 2, и т. д. и обозначить дуги, исходящие из узла i и входящие в узел j, парой номеров (i, j). Последовательность дуг (без учета их ориентации), соединяющая узлы i и j, называется пу­тем между этими узлами.

Если i = j, то путь называется контуром. Сеть является связной при условии, что существует по крайней мере один путь между любой па­рой узлов. Сеть, содержащая Р узлов и Р-1 дуг носит название де­рева и не содержит контуров.

При определении сети задают пропускную возможность дуг U_ij ≥0 по отношению к общему потоку, выходящему из узла i и входя­щему в узел j. Ранее, при решении транспортной задачи величина U_ij принималась равной бесконечности, либо нулю. В первом случае это оз­начало, что никаких ограничений на величину потока по дуге не накла­дывалось, а во втором - что поток непосредственно между узлами i и j не допускается.

Кроме этого, в прикладных задачах, сеть дополнительно характери­зуется величиной чистого потока и стоимостью доставки единицы потока из узла i в узел j, т. е. стоимостью единичного потока по дуге (i, j). Если значение величины чистого потока Q_k положительно, то из узла должно выходить на Q_k единиц потока больше, чем входить в него, и наоборот, когда значение Q_k отрицательно. Если значение Q_k равно нулю, то весь поток, входящий в узел, равен потоку, выходящему из него.

Если С_ij - стоимость единицы потока из узла i в узел j, а Х_ij - вели­чина потока по дуге (i, j) в течение планового периода, то общей опти­мизационной сетевой задачей является задача минимизации

при ограничениях

Ограничения (8.74) называют уравнениями сохранения потока или уравнениями материального баланса.

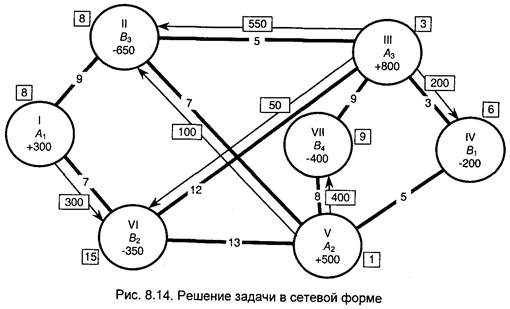
На рис. 8.14 изображены кружками 3 поставщика и 4 потребителя некоторой продукции. Все вершины пронумерованы римскими цифрами. Мощности поставщиков отмечены положительным знаком (плюсом), спросы потребителей - минусами. Вершины соединены линиями, по­казывающими, что между соответствующими пунктами имеются дороги (участки транспортной сети), называемые дугами. Каждой дуге соответ­ствует число С_ij, являющееся показателем принятого в задаче крите­рия оптимальности (расстояние, стоимость перевозки и т. д.). Рисунки могут изображать, а могут и не изображать транспортную сеть в реаль­ном масштабе.

Решение, как и в матричном алгоритме, начинается с базисного рас­пределения поставок. Произвольно, начиная с вершины I, начинаем рас­пределять поставки. К вершине примыкает две дуги. Показатель С_ij ду­ги I-VI меньше, чем дуги 1-II, поэтому целесообразно из вершины I вы­возить продукцию по этой дуге.

Поставки из одной вершины в другую обозначают стрелками, указы­вая в них объем поставок. Стрелка показывает направление перемещения продукции.

Рисуем стрелку от вершины I к вершине VI и указываем в ней объем поставки 300 единиц. Вершине VI необходимо дополнительно поставить еще 50 единиц. Эта вершина соединена с поставщиком, расположенным в вершине III и VI. Из вершины III направляем в вершину VI недостающие там 50 единиц и т. д.

Полученный базисный план поставок, должен удовлетворять сле­дующим требованиям:

каждая мощность должна быть распределена, а каждый спрос должен быть удовлетворен;

к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;

общее количество стрелок должно равняться количеству вершин ми­нус единица (Р -1). Количество стрелок зависит только от количества вершин, количество дуг не имеет значения;

стрелки не должны образовывать замкнутую цепь, т. е. не должно быть так, что, начав движение из какой-либо вершины по стрелке и пере­ходя от одной стрелки к другой (не обращая при этом внимание на их на­правление), можно было бы вернуться в ту же вершину;

любые две вершины могут соединяться только одной дугой, т. е. если между двумя соседними пунктами имеется более одной дороги, то на графике и при решении задачи должна быть выбрана только одна.

Полученное базисное распределение проверяется на оптимальность с помощью потенциалов. Вершине I присваиваем произвольно потенциал, например, 8 и записываем его в квадрат около этой вершины. От верши­ны I отходит одна стрелка. Прибавив к ее потенциалу показатель С_ij, со­ответствующий дуге I—VI, получаем потенциал вершины VI (8 + 7 = 15). К вершине VI подходит стрелка от вершины III. Ее направление проти­воположно направлению нашего движения, поэтому показатель, со­ответствующий данному ребру не прибавляется, а вычитается из потен­циала вершины VI. Потенциал вершины III будет равен 15-12 = 3 и т. д.

Правило получения потенциалов вершин сформулируется следующим образом. Сначала любой произвольно выбранной вершине присваивается любой произвольно выбранный потенциал. Чтобы не иметь отрицатель­ных значений потенциалов, принимают значение первого потенциала достаточно большое. Двигаясь только по стрелкам, определяют потен­циалы остальных вершин. Если стрелка выходит из вершины, то к по­тенциалу этой вершины прибавляется значение С_ij. Если направление стрелки противоположно, то показатель С_ij вычитается из потенциала вершины.

Значение целевой функции определяется суммой произведений показателей мощности и спросов на соответствующие им потенциалы

300-8-650-8+ 800-3-200-6 + 500-1-350-15-400-9 = -9950.

Значение целевой функции получается отрицательным.

Для определения оптимальности базисного распределения опреде­ляются характеристики дуг. При оптимальном плане характеристики дуг, имеющих стрелки, должны равняться нулю, а дуги без стрелок - по­ложительным величинам. Наличие хотя бы одной отрицательной дуги без стрелки указывает на неоптимальность базисного распределения, т. е. при оптимальном распределении

где: С_ij - критерий оптимальности;

u_i - наибольший потенциал вершины;

v_j - значение меньшего потенциала вершины.

В нашей задаче дуга VI-V имеет одну отрицательную характери­стику, что говорит о том, что базисное распределение можно улучшить.

Перераспределение поставок производится так, чтобы одна из по­ставок попала на дугу, имеющую отрицательную характеристику. Для перераспределения поставок составляется цепь (называемая часто кон­туром). Цепь представляет собой замкнутую фигуру, состоящую из ду­ги без стрелки и дуг со стрелками. Новая стрелка направляется от вер­шины с меньшим потенциалом к вершине с большим потенциалом. Рассматриваются все стрелки в цепи, направление которых противопо­ложно направлению новой стрелки. Среди них выбирается стрелка с меньшей поставкой, и это значение прибавляется ко всем поставкам в стрелках, имеющих то же направление, что и новая стрелка, и вычитается из поставок в стрелках, имеющих противоположное направление. По­ставки в стрелках, не входящих в цепь, сохраняются неизменными.

В нашем примере мы получим цепь VI—V—II—III—VI. Величина по­ставки 50 ед. прибавляется к поставкам дуги II-III и вычитается из дуги II-VI. Выбранная ранее стрелка с противоположной поставкой ликвиди­руется. Общее количество стрелок остается неизменным. Очередная проверка показывает, что новый базисный план получился оптимальным.

Если при полном использовании мощностей и полном удовлетворе­нии спроса количество стрелок оказывается меньше, чем Р -1, то задача оказывается вырожденной. Способ борьбы с вырождением заключается в том, что вводятся дополнительные стрелки с нулевыми поставками. Совершенно безразлично, из положительной или отрицательной вер­шины будут выходить, и входить стрелки. Важно, чтобы стрелки не образовывали замкнутую цепь.

При сетевой постановке задач задаются не только поставщики и потребители, но могут задаваться и пункты пересечения участков - вер­шин, в которых нет ни поставщиков, ни потребителей. Наличие таких нулевых вершин не меняет способа решения. Им присваиваются по­тенциалы на тех же основаниях, что и другим вершинам, но их спрос или предложение равны нулю.

Результаты решения транспортных задач на сети и по матрице совпа­дают только в том случае, если не учитываются ограничения пропускной возможности дорог. В матричных алгоритмах каждый поставщик и по­требитель может быть соответственно только отправителем или получа­телем груза. Движение груза через поставщика или через другого потре­бителя в явном виде невозможно. При сетевой постановке задачи движе­ние груза из одного пункта в другой выбирается в ходе самого расчета.

Когда при матричной постановке задачи говорят, что из пункта i в пункт j можно перевезти не более такого-то объема груза, то на самом деле это означает лишь невозможность перевозки большего количества груза по наивыгоднейшему пути между этими пунктами. Блокируя такой путь для большего объема груза, мы не рассматриваем возможность передвижения груза между этими пунктами по другим дорогам, так как в действительности ограничения распространяются на какие-то участки дороги. Поэтому запись ограничений пропускной возможности при се­тевой постановке задачи больше соответствует реальным условиям, а следовательно, и дает истинный оптимум.

Для решения на сети транспортной задачи при небалансе мощно­сти и спроса необходимо, как и в матричных алгоритмах, ввести фик­тивного потребителя со спросом, равным небалансу. Фиктивный по­требитель соединяется дугами одинаковой длины непосредственно со всеми поставщиками. Величина показателя дуг должна быть относи­тельно большой, чтобы фиктивные пункты не могли стать промежу­точными пунктами сети.

СИМПЛЕКСНЫЙ МЕТОД

ОБЩИЕ ПОЛОЖЕНИЯ

Симплексный метод - это универсальный метод линейного программирования, в котором осуществляется направленное движение по базисным планам до нахождения оптимального решения. При рас­смотрении этого метода важно не только установить последовательность действий при решении оптимизационных линейных моделей, но и опре­делить системный подход, позволяющий анализировать любую конкрет­ную модель.

Когда рассматриваемая модель содержит т уравнений ограничений, вычислительная процедура симплексного метода за­ключается в следующем:

Шаг 1. Выберем т переменных, задающих допустимое пробное ре­шение. Исключим эти переменные из выражения для целевой функции.

Шаг 2. Проверим, нельзя ли за счет одной из переменных, прирав­ненных вначале к нулю, улучшить значение целевой функции, прида­вая ей отличные от нуля (причем только положительные) значения. Если это возможно, перейдем к шагу 3. В противном случае прекра­тим вычисления.

Шаг 3. Найдем предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из т переменных, вошед­ших в пробное решение, не обратится в нуль. Исключим из выражения для целевой функции только что упомянутую переменную и введем в пробное решение ту переменную, за счет которой результат может быть улучшен.

Шаг 4. Разрешим систему т. уравнений относительно переменных, вошедших в новое пробное решение. Исключим эти переменные из вы­ражения для целевой функции. Вернемся к шагу 2.

Симплексная вычислительная процедура формальна, и ее использо­вание не обязательно должно связываться с конкретным содержанием задачи. Ниже приведено несколько типичных задач, решаемых сим­плексным методом.

Задача 8.9. Корма трех видов В₁, В₂, В₃ содержат определенное количество питательных веществ А₁, А₂, A₃. Цены, по которым поку­паются эти корма, различны. Требуется составить кормовой рацион, со­стоящий из указанных кормов, так, чтобы в нем было не менее заданных ко­личеств питательных веществ и чтобы он был самым дешевым.

Задача 8.10. Есть три вида станков: А₁, А₂, А₃. На этих станках по­следовательно обрабатываются детали четырех видов: В₁, В₂, В₃, б₄. Известно сколько часов каждая деталь изготавливается на каждом стан­ке, сколько времени может проработать каждый станок и какая при­быль может быть получена от продажи детали каждого типа. Требуется найти оптимальный план работы станков, чтобы получить максималь­ную прибыль.

Задача 8.11. Имеются автомобили трех типов А_1; A₂, A₃, рабо­тающие на перевозке однородного груза у трех потребителей В₁, В₂, В₃. Известна производительность каждого автомобиля у каждого по­требителя и себестоимость использования автомобиля. Требуется так закрепить автомобили за потребителями, чтобы была наименьшая се­бестоимость (максимальная производительность) и др.

Не нашли, что искали? Воспользуйтесь поиском: