Элементы теории ошибок. В основе теории ошибок лежат два предположения, подтверждаемые на опыте.

В основе теории ошибок лежат два предположения, подтверждаемые на опыте.

1. При большом числе измерений случайные ошибки (погрешности) одинаковой величины, но разного знака встречаются одинаково часто.

2. Большие погрешности встречаются реже, чем малые, то есть вероятность появления погрешности уменьшается с ростом величины погрешности.

В этом разделе опишем – с пояснениями, но без доказательств – основные правила обработки случайных погрешностей.

Рассмотрим ситуацию обработки прямых измерений на примере измерения массы некоторого тела.

Таблица 1.

№	mi (кг)	Δ mi (кг)	(Δ mi)2
	m 1		()2
	m 2		()2
...	………………….	…………………..	…………………..
n	mn		()2

В качестве наилучшего значения для измеряемой величины обычно применяют среднее арифметическое значение из всех полученных результатов:

,

где n – число измерений.

Из математической статистики следует, что этому результату следует приписать погрешность, определяемую формулой:

.

Результат опыта записывается в виде:

кг.

Теория погрешностей говорит нам о том, что «ошибка в определении ошибки примерно равна самой ошибке». Поэтому погрешность результата не столько определяют, сколько оценивают.

Оценка Δ m подобрана таким образом, что при проведении многочисленных серий измерений погрешность в 2/3 случаев (точнее в 0,683) оказывается меньше Δ m, а в 1/3 случаев больше, чем Δ m. Погрешность, определенную таким образом, обычно называют стандартной или среднеквадратичной погрешностью опытов. В математической статистике среднеквадратичную погрешность обозначают греческой буквой σ (сигма), а квадрат этой величины называется дисперсией. Интервал значений от () до (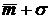) носит название доверительного интервала.

Если пользоваться терминологией теории вероятностей, то можно сказать, что с вероятностью (надежностью) α ≈ 2/3, результат измерений не выходит за пределы доверительного интервала.

Погрешность измерений может быть выбрана как 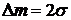. В этом случае при бесконечно большом количестве опытов надежность α = 0,954, или только в в 5% случаев результаты опыта оказываются за пределами интервала . Если погрешность выбирается как , то α = 0,970 и практически невероятно, чтобы результаты измерений оказались за пределами интервала .

Отсюда следует практическое правило для определения промахов при обработке результатов измерений. Промахами считаются результаты измерений, оказавшиеся за пределами интервала . Промахи исключаются, и результаты измерений обрабатываются заново. После вторичной обработки результатов вновь производится проверка на промахи, и если они обнаруживаются, то результаты обрабатываются третий раз т. д., до полного исключения промахов.

Если число измерений n достаточно велико, то столбец в первой таблице имеет смысл обработать так, как столбец во второй таблице. Здесь следует суммировать отдельно и , и полученные суммы алгебраически сложить. Полученный близкий к нулю результат будет свидетельствовать о правильности произведенных измерений и безошибочном вычислении .

Косвенные измерения в нашем лабораторном практикуме будут обрабатываться как прямые измерения (см. таблицу 2). Теория [3] говорит о том, что это допустимо, если результаты измерений не сильно отличаются от соответствующего среднего значения.

С более строгой теорией обработки косвенных измерений Вы познакомитесь в лаборатории механики. Там же Вы научитесь учитывать систематические погрешности.

Описание установки

Структурная схема установки представлена на рис. 1.

Рис. 1

В состав экспериментальной установки входят:

1 – генератор электрических колебаний звуковой частоты;

2 – счетчик импульсов;

3 – секундомер;

4 – резистор ограничительный R = 500 Ом;

5 – ключ телеграфный усовершенствованный.

Генератор 1 вырабатывает гармонические электрические колебания звуковой частоты. Частота этих колебаний f определяется с помощью счетчика импульсов и секундомера, в качестве которых используются два однотипных электронных счетчика-секундомера ССЭШ (счетчик-секундомер электронный школьный). Один из них используется в режиме счета импульсов, а второй – как секундомер. Соответствующие переключения в ССЭШ интуитивно понятны и здесь не описываются.

Счетчик импульсов 2 через ограничительный резистор 4 соединен с выходом звукового генератора 1. Ниже (в первом задании) описана процедура регулировки амплитуды выходного напряжения генератора для уверенного срабатывания счетчика импульсов. Срабатывание счетчика происходит только в положительные полупериоды выходного переменного напряжения, то есть один раз за каждый период. Счетчик имеет три пересчетные декады, и, следовательно, его емкость равна 999 импульсов.

Одновременно с включением счетчика импульсов должен включаться и секундомер 3. Точность используемого секундомера 0,01 с, а диапазон измеряемого времени 0,01 – 9,99 сек.

Управление установкой осуществляется с помощью усовершенствованного телеграфного ключа. Запускается установка нажатием на ключ, а останавливается при его отпускании. Зазор между контактами телеграфного ключа должен быть установлен минимальным; чем он меньше, тем точнее совпадает момент включения счетчика с моментом включения секундомера. Сброс показаний после каждого измерения производится вручную нажатием кнопок «Сброс» на счетчике и секундомере.

Не нашли, что искали? Воспользуйтесь поиском: