
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример построения лексического анализатора.
<идентификатор>::=<буква><буква или цифра>*
<буква>:: =а|b|...|2. <цифра>::=0|1|...|9 <число>::=<цифра>*
Столбцы 1 и 2 заполнены уже на входе, столбцы 3 и 4 на выходе лексического анализа.
| Входная строка | Выходная строка | |||||
| Ключевые слова | Разделители | Имена | Константы | Текст программы | Лексическая свертка | |
| LI=3 | LC = 3 | |||||
| abs | + | lab1 | program lab1 var s, i: integer; begin s:=0; for i:=1 to 10 do s:=s+i*i; end. | 13 30 14 31 27 32 29 15 28 11 31 26 40 28 17 32 26 41 18 24 19 31 26 31 20 32 22 32 28 12 | ||
| begin | - | s | ||||
| end | * | i | ||||
| program | / | |||||
| var | ( | |||||
| integer | ) | |||||
| real | := | |||||
| for | , | |||||
| to | ; | |||||
| do | : |
4. СИНТАКСИЧЕСКИЙ АНАЛИЗ.
4.1. Автоматы с магазинной памятью (МП – автоматы, МПА). (АУ-192)
МПА P есть семерка вида (Q, S, G, d, q 0, z 0, F), где Q – множество состояний автомата,
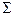 - входной алфавит, Г – магазинный алфавит, d: Q´(S È { e })´Г ®2Q´G* - функция переходов, q 0 Î Q – начальное состояние, z 0 ÎG - начальный символ в магазине, F Î Q - множество финальных состояний автомата. В магазин можно писать(читать) только верхний символ.
- входной алфавит, Г – магазинный алфавит, d: Q´(S È { e })´Г ®2Q´G* - функция переходов, q 0 Î Q – начальное состояние, z 0 ÎG - начальный символ в магазине, F Î Q - множество финальных состояний автомата. В магазин можно писать(читать) только верхний символ.
Конфигурация автомата есть тройка (q, w, a) Î Q ´S*´G*, где q – текущее состояние,  - часть цепочки,
- часть цепочки, 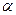 - содержимое всего магазина (верхним символом является самый левый?).
- содержимое всего магазина (верхним символом является самый левый?).
Такт работы автомата - это бинарное отношение на множестве конфигураций.
(q, aw, za) ⊢ (q¢, w, ga), если (q ¢, g) Î d (q, a, z). Такт невозможен, если a = e, т.е. магазин пуст.
Начальная конфигурация (q 0, w, z 0). Заключительная конфигурация (q, e, a), q Î F, a ÎG*.
Цепочка допускается МП - автоматом, если из начальной конфигурации автомат может перейти в заключительную конфигурацию, т.е. (q 0, w, z 0) ⊢ * (q, e, a), q Î F.
Язык, определенный автоматом, есть множество цепочек, допускаемых автоматом.
L (P) = {w | (q 0, w, z 0) ⊢ * (q, e, a)}.
Для любой КС–грамматики G и порождаемого ей языка $ МП–автомат, что L (G) = L (P).
За один такт МП–автомат может заменить лишь один верхний символ магазина.
Автомат считается расширенным, если он за один такт может заменить цепочку.
Автомат P допускает цепочку w ÎS* опустошением магазина, если (q 0, w, z 0) ⊢ + (q, e, e),
Le (P) - множество таких цепочек. Если P – МП–автомат, то 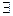 P¢: Le (P) = L (P ¢).
P¢: Le (P) = L (P ¢).
Теорема. Утверждения (1)-(4) эквивалентны. (АУ-210)
(1) L = L (G) для КС–грамматики G (2) L = L (P 1) для некоторого МПА P 1
(3) L = Le (P 2) для некоторого МПА P2 (4) L = L (P 3) для некоторого расширенного МПА P3
МПА P *= (Q, S, G, d, q 0, z 0, F) называется детерминированным, если " q Î Q, " a ÎS и " z Î G
| d (q,a,z) | + | d (q,e,z) | £ 1. Существуют КС-языки, которые нельзя определить детерминированными МПА. Но есть класс LR (k) КС-грамматик, для которого $ ДМПА.
Для ДМПА будем писать d (q, a, z)=(r, g) вместо {(r, g)}.
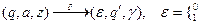 0 –лента осталась на месте, 1 – символ ленты прочитан.
0 –лента осталась на месте, 1 – символ ленты прочитан.
Пример: G0=({ а,+,*,(,)}, { Е, Т, F }, Е, Р), где Р = { Е ® Е + Т | Т, Т ® Т * F | F, F ® (Е) | а }
Построим недетерминированный автомат, допускающий язык L (G 0). (АУ-204? 209? 328? 342?)
Пусть A – начальное, C – рабочее, а D – заключительное состояния автомата,
b - любой терминальный символ, $ – начальный символ магазина.
1. (A, b, $)® { (0, C, E $) } 4. (C, b, F)® { (0, C, (E)), (0, C, a) }
2. (C, b, E)® { (0, C, E+T), (0, C, T) } 5. (C, b, b)® { (1, C, e) }
3. (C, b, T)® { (0, C, T*F), (0, C, F) } 6. (C, e, $)® { (0, D, e) }
т.е. мы можем в магазине заменять символ на цепочку в соответствии с правилами КС-грамматики. На вход автомата поступает цепочка a + a * a.
(A, a+a*a, $) ⊢ 1 (C, a+a*a, E $) ⊢ 2 a (C, a+a*a, E+T $) ⊢ 2 b (C, a+a*a, T+T $) ⊢ 3 b (C, a+a*a, F+T $)
⊢ 4 b (C, a+a*a, a+T $) ⊢ 5 (C, +a*a, +T $) ⊢ 5 (C, a*a, T $) ⊢ 3 a (C, a*a, T*F $) ⊢ 3 b (C, a*a, F*F $)
⊢ 4 b (C, a*a, a*F $) ⊢ 5 (C, *a, *F $) ⊢ 5 (C, a, F $) ⊢ 5 (C, a, a $) ⊢ 5 (C, e, $) ⊢ 6 (D, e, e)
Т.о. цепочка допускается этим недетерминированным! МП-автоматом. Сложность задачи синтаксического анализа состоит в том, чтобы догадаться, какое из правил применить. Детерминированный автомат или только читает, или только не читает.???
Можно ли для G 0 предложить детерминированный автомат? Да, но расширенный. Как связан МПА с деревом вывода КС-грамматики? В выводе МП-автомату надо как можно быстрее получить в магазине самый левый символ, равный самому левому символу ленты. Разобьём терминалы на классы: b Î{ a,+,*,(,)}; d Î{ a,+,*,(,), e }; m Î{+,(,$}; s Î{(,$}; t Î{+,), e?}; k Î{ a, e?)}.
По-прежнему A, С и D – начальное, рабочее и заключительное состояния автомата.
1. (A, b, $)® (1, C, b $) 6. (C, t, T+E)® (0, C, E) 11. (C, *, T)® (0, C, * T)
2. (C, d, a)® (0, C, F) 7. (C, t, Ts)® (0, C, Es) 12. (C, k, *)® (1, C, k *)
3. (C, d, )E()® (0, C, F) 8. (C, t, E)® (1, C, tE) 13. (C, e, ()® (1, C, $)?
4. (C, d, F*T)® (0, C, T) 9. (C, ), E)® (1, C, )E) 14. (C, e, E $)® (0, D, e)
5. (C, d, Fm)® (0, C, Tm) 10. (C, b, +)® (1, C, b +)
(A, a+a*a, $) ⊢ 1 (C, +a*a, a $) ⊢ 2 (C, +a*a, F $) ⊢ 5 (C, +a*a, T $) ⊢ 7 (C, +a*a, E $) ⊢ 8
(C, a*a, +E $) ⊢ 10 (C, *a, a+E $) ⊢ 2 (C, *a, F+E $) ⊢ 5 (C, *a, T+E $) ⊢ 11 (C, a, *T+E $) ⊢ 12
(aC, e, a*T+E $) ⊢ 2 (C, e, F*T+E $) ⊢ 4 (C, e, T+E $) ⊢ 6 (C, e, E $) ⊢ 14 (D, e, e)
4.2. 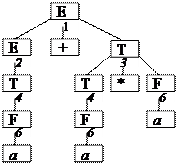 Нисходящий анализ.
Нисходящий анализ.
Пример: G0.
Выпишем левый разбор цепочки: 12463466.
Теперь правый разбор: 13646246.
Обычно правый разбор записывают в обратной форме:64264631.
Построим дерево поиска (левое). E
1  2
2
E+T T
1  2 3
2 3  4
4
E+T+T T+T T*F F
1  2 3
2 3  4 3
4 3  4 5
4 5  6
6
E+T+T+T T+T+T T*F+T F+T T*F*F F*F (E) a
Если грамматика имеет левую рекурсию, то процесс поиска может быть бесконечным, но если у неё правая рекурсия, то левое дерево поиска конечно. aÎ(S=ΣTÈ ΣN)*, w ÎS*.?
Если w Î L (G), то алгоритм СНАЧАЛА ВШИРЬ найдет её за конечное время.
Терминальным префиксом цепочки 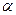 называется такой x Î ΣT*, что.a = xyz, y Î ΣN, z Î Σ*.
называется такой x Î ΣT*, что.a = xyz, y Î ΣN, z Î Σ*.
a согласуется с w, если терминальный префикс цепочки a является префиксом w.
В дереве будем стараться выбирать те вершины, у которых длина согласованной с искомой цепочкой части максимальна.
Алгоритм нисходящего МП-распознавателя. (АУ-326?)
Предполагается, что нет левой рекурсии.
Пользуемся: если цепочка не согласуется с входной цепочкой, то её не раскрываем.
1.Инициализация (выписываем корневую вершину).
2.Вниз по дереву поиска.
а) Вершина из стека объявляется текущей и удаляется из стека.
б) Если текущая цепочка не согласуется с входной цепочкой, то идти ВБОК.
Иначе если текущая цепочка совпадает с входной, то УСПЕХ,
иначе породить дочерние вершины, упорядочить их (по применимости правил) и записать в стек, идти ВНИЗ.
3.ВБОК:
Пример: Е1 – к Е применили 1-ое правило, если пошли ВБОК, то Е(1+1)=Е2
Имеем 2 стека: 1-й - Е1, 2-й – Е+Т, $
После применения ВБОК: 1-й – Е2, 2-й – Т, $
Попытка применить другое правило к тому же самому нетерминальному символу. Если другое правило есть, то увеличили цифру и ВНИЗ, иначе стираем букву, пытаемся увеличить цифру предыдущего, ВВЕРХ.
4.ВВЕРХ. Если вверх некуда, т.е. в стеке достигли дна (пуст), то НЕУДАЧА, иначе собственно ВВЕРХ.
НЕУДАЧА – слово не может быть порождено в грамматике, сообщение об ошибке, невозможности вывода.
УСПЕХ – во втором стеке записан левый разбор.
Замечания:
1.Алгоритм имеем плохие возможности локализации ошибки.
2.Алгоритм имеет экспоненциальную трудоёмкость, поэтому надо:
а) пусть грамматика не содержит правил с пустой правой частью, можно не рассматривать вершину с длиной цепочки;
б) правила упорядочивать по возрастанию вероятности использования.
3.Перед тем как строить дерево, подумайте, А СТОИТ ЛИ ЭТО ДЕЛАТЬ?
Если грамматика является LL(k)-грамматикой, то поиск закончится за линейное время.
4.3. Алгоритм Кока-Янгера-Касами. (АУ-352)
Полиномиальный алгоритм для любых грамматик. Трудоемкость O (n 3), память О (n 2), n =|  |.
|.
Вход: КС- грамматика в НФХ, без е -правил, входная цепочка w ÎS+, w = w 1 w 2… wn.
 Выход: таблица разбора Т для w. Нетерминал A Î tij Û AÞ+ wi … wj + i -1 = часть входной цепочки, начиная с i -го элемента, длиной j. j =1, n, j =1, n - i +1.
Выход: таблица разбора Т для w. Нетерминал A Î tij Û AÞ+ wi … wj + i -1 = часть входной цепочки, начиная с i -го элемента, длиной j. j =1, n, j =1, n - i +1.
Пример: G: S 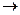 АА | АS | b А
АА | АS | b А 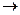 SА | AS | a
SА | AS | a  = abaab.
= abaab.
| A | S | A Î t 11 Û A Þ+ w 1 = a | ||||||
| 5,1 | 1,1 | S Î t 21 Û S Þ+ w 2 = b | ||||||
| A | S | A | S | A Î t 12 Û A Þ+ w 1 w 2 = ab | ||||
| 5,1 | 2,1 | 4,1 | 1,2 | S Î t 23 Û S Þ+ w 2… w 4 = baa | ||||
| A | S | S | A | S | t 23 k=1= t 21+ t 32, t 21´ t 32 ={ SS } | |||
| 4,2 | 1,1 | 1,2 | 5,1 | 2,1 | k=2= t 22+ t 31 | t 22´ t 31 ={ AA } | ||
| A | S | A | S | A | S | |||
| 5,1 | 2,1 | 4,1 | 1,1 | 5,1 | 2,1 | |||
| A / 6 | S / 3 | A / 6 | A / 6 | S / 3 | ||||
Дерево разбора:
1. Положим ti 1 = { A: (A® ai)Î P } " i. Пусть известны tik " k = 1.. j -1.
2. Вычислим tij = { A | $ k Î1.. j -1 & (A ® BC) Î P & B Î tik & C Î ti+k , j-k }.
3. Повторять шаг 2, пока не заполним всю таблицу.
Замечания:
1.Если S Î t 1 n Û w Î L (G).
2.Желательно найти левый вывод. Можно в 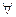 клетке указывать способ деления и правило.
клетке указывать способ деления и правило.
3.Есть алгоритм Эрли, для однозначных грамматик-Т=О(n 2), для LL-грамматик-Т=О(n).
4.4. LL-грамматики и LL-распознаватели. (АУ-376)
Рассмотрим алгоритм для LL- грамматик с линейным временем и линейной памятью. Сложность состоит в том, что не всякая грамматика может быть приведена к LL-форме. Более того, даже вопрос «приводима ли грамматика к LL–форме?» алгоритмически неразрешим.
Определения:
1. Пусть a - левовыводимая цепочка в грамматике G, причем a = xb, x ÎST*, b ÎSNS?*È{ e }. Тогда х - терминальный префикс цепочки a (ее обработанная, законченная часть!).
2. Пусть k - целое, a ÎS* - левовыводимая в грамматике G цепочка. Определим функцию
FIRST k (a) = {wÎST*| либо | w |< k & a Þ* w, либо | w |= k & a Þ* w x, для некоторого x ÎS*}, т.е. все терминальные начала длины £ k.
3. КС-грамматика G называется LL (k) -грамматикой для некоторого k, если из w, x, y ÎST* и существования 2-х левых! выводов
а) S Þ* wAa Þ wba Þ* w х и б) S Þ* wAa Þ wga Þ* wy,
для которых FIRST k (х) =FIRST k (y), следует b = g.
Второе определение: (A ® b),(A ® g)Î P & S Þ* wAa следует, что FIRST k (ba)ÇFIRST k (ga)=Æ.
В частности, грамматика без е -правил G Î LL(1) Û FIRST1(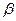 )
) 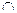 FIRST1(
FIRST1(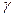 )=Æ для всех A ÎSN.
)=Æ для всех A ÎSN.
Заметим, что если в грамматике есть правило с левой рекурсией, то должно быть и правило, выходящее из неё. В этом случае FIRST1(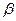 )
) 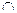 FIRST1(
FIRST1(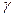 )≠Æ и GÏLL(1).
)≠Æ и GÏLL(1).
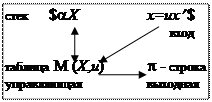 k -предсказывающий алгоритм разбора: (АУ-385)
k -предсказывающий алгоритм разбора: (АУ-385)
Пусть на входе цепочка x = ux ¢$,
u =FIRST k (х) – аванцепочка из k символов.
Конфигурацию удобно задавать как (х, Xa $, p),
где Xa -цепь в стеке; p - цепь на выходе.
Начальная конфигурация задается (w$, x 0$, e), где х 0-начальный символ грамматики.
1.Если М(X, u)=(b, i), то (х, Xa, p) ⊢ (х, ba, pi), т.е. в стеке замена X ® b, на выход пишем pi.
2. Если М(X, u)= выброс & x = ax ², то (х, aa, p) ⊢ (х ², a, p), т.е. в стеке и на входе удаляем a.
3. Если (w$, x 0$, e) ⊢ * ($,$,p), т.е. алгоритм достигает финальной конфигурации ($,$, p), то работа прекращается и цепочка p является левым разбором входной цепочки w.
4.Если алгоритм достигает конфигурации (x, Xa,p) и М(X, u)= ошибка, то конфигурация (текущая) объявляется ошибочной, разбор прекращается и выводится сообщение об ошибке.
Предсказывающий алгоритм корректен для G, если L(G)={ w | A (w)-определен} и А (w)=p?.
Построение корректной управляющей таблицы M для LL(1) грамматик. Пусть FOLLOW 1(b) = {w | SÞ*abg & wÎ FIRST 1(g)}, т.е. множество терминалов, которые могут встречаться непосредственно справа от b (= следовать за b) в любых выводимых цепочках, причем если ab - выводима, то e Î FOLLOW 1(b). Сначала строят FIRST 1(X) и FOLLOW 1(A).
Если правило A®a имеет номер i, то М(А, а) = i " a Î FIRST 1(a) \ { e }.
Если e Î FIRST 1(a), то М(А, b) = i " b Î FOLLOW 1(A).
M(a, a) = выброс " a ÎST, M($, e) = допуск, M(X, a) = ошибка в остальных случаях.
Если хотя бы в одной клетке таблицы окажется более одного номера, то грамматика ÏLL(1).
Для правого разбора алгоритм похожий, но таблицу для LR строить значительно сложнее.
Определим множества L (A) = { x ÎS | AÞ+ xa } и R (A) = { x ÎS | AÞ+ bx }: сначала построим множества символов l (A) = l 0(A) и r (A) = r 0(A), являющихся самыми левыми (правыми) во всех A -правилах, а затем множества li +1(A) = È lk (B), ri +1(A) = È rk (C), " k £ i, " B Î li (A), " C Î ri (A)
| l 0 | l 1 | l 2 | L | r 0 | r 1 | r 2 | R | |
| E | ET | F | (a | ETF(a | T | F | ) a | TF)a |
| T | TF | (a | TF(a | F | ) a | F)a | ||
| F | (a | (a | ) a | )a |
L (A) = È lk (A), R (A) = È rk (A). Построим множества L и R для грамматики G0. Чтобы получить множества FIRST 1(A), достаточно удалить из L (A) все нетерминальные символы. Для всех нетерминалов грамматики G0 имеем FIRST 1={ (, a }, в т.ч. и для E-правил FIRST 1(Е + Т)= FIRST 1(Т) Þ G0ÏLL(1).
G0: { Е® Е+Т | Т, Т® Т*F | F, F® (Е) | а } ÏLL(1), т.к. она леворекурсивна. Ну и что?
Пример LL(1) грамматики (ГМ-479). Грамматика является LL(1) грамматикой, если для распознавания очередного правила достаточно заглянуть на входной ленте на один символ вперед.
G0′: { S® ТR 1, R® +ТR 2| е 3, Т® EF 4, F® *EF 5| е 6, E® (S) 7| а 8} ÎLL(1). Для построения таблицы М нужна функция FIRST 1, а ее проще строить по грамматике без е -правил. Удалив е -правила, получим грамматику G0″ ÏLL(1) - первые терминальные символы разных R- и F-правил совпадают: { S® Т | ТR, R® +Т | +ТR, Т® E | EF, F® *E | *EF, E® (S) | а }.
| r | l 0 | l 1 | l 2 | FIRST1 | r -1 | F 0 | f 0′ | f 0″ | f 1 | f 1′ | f 1″ | f 2 | f 2′ | f 2″ | FOLLOW1 | |
| S | R | T | E | (a | (a | )$ | )$ | |||||||||
| R | Rе | + | + | SR | )$ | )$ | ||||||||||
| T | F | E | (a | (a | R | + | )$ | +)$ | ||||||||
| F | Fе | * | * | TF | R + | )$ | +)$ | |||||||||
| E | ) а | (a | (a | F | * | R + | )$ | *+)$ |
FIRST 1(A) = (L (A) = È lk (A)) \ SN.
Что может следовать за E? Очевидно, только F, начинающееся с ‘*’, или превращающееся в e. А что за e? В этом случае E и F образуют T, и за E будет то, что следует за T, т.е. R, начинающееся с ‘+’, или равное e. Тогда за E, входящим в S, следует ‘$’, или ‘)’.
Пусть S e = {A | (A® e)ÎP} = {R,F} – множество нетерминалов, для которых $ e -правило.
r -1(A) = {B | AÎ r (B)}– множество таких B, что $ B-правило с последним символом A.
F 0(A) – множество символов, непосредственно следующих в правилах за A, и еще $ для S.
fi ′(A) = È FIRST 1(B) " B Î[SN Ç Fi (A)], Fi ′(A) = Fi (A) È fi ′(A) EMPTY = { A ÎSN | A Þ* e }
fi ″(A) = È Fi ′(B) " B Î[S e Ç Fi ′(A)], Fi ″(A) = Fi′ (A) È fi ″(A) У нас EMPTY = S e.
fi +1(A) = È Fi ″(B) " B Î[S N Ç r -1(A)], Fi +1(A) = Fi″ (A) È fi +1(A) FOLLOW 1(A) = F ¥(A) \ SN
FIRST 1(A 1 …An) = FIRST 1(A 1) È { if A1Î EMPTY then FIRST 1(A 2) } È …
правило имеет вид A ® x Þ " v Î FIRST 1(x), а если A ® e Þ " v Î FOLLOW 1(A).
В верхней части таблицы для каждого нетерминала A мы пишем номер i его правила Pi в ячейке M(A, v), если Pi =(A ® x) & v Î FIRST 1(x), или Pi =(A ® e) & v Î FOLLOW 1(A). Иначе - “ ошибка ”!
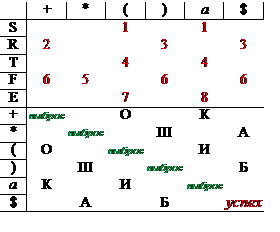 Продолжение примера G0′. Вход: a + a * a. Управляющая таблица для LL (1)-грам-ки G0′
Продолжение примера G0′. Вход: a + a * a. Управляющая таблица для LL (1)-грам-ки G0′
| Стек | Вход | № правила | Правая часть | Комментарии |
| $ S | a+a * a $ | TR | a Î FIRST 1(S) | |
| $ RT | a + a * a $ | EF | a Î FIRST 1(T) | |
| $ RFE | a + a * a $ | a | a Î FIRST 1(E) | |
| $ RFa | a + a * a $ | выброс | ||
| $ RF | + a * a $ | e | +Î FOLLOW 1(F) | |
| $ R | + a * a $ | + TR | +Î FIRST 1(R) | |
| $ RT + | + a * a $ | выброс | ||
| $ RT | a * a $ | EF | a Î FIRST 1(T) | |
| $ RFE | a * a $ | a | a Î FIRST 1(E) | |
| $ RFa | a * a $ | выброс | ||
| $ RF | * a $ | * EF | *Î FIRST 1(F) | |
| $ RFE* | * a $ | выброс | ||
| $ RFE | a $ | a | a Î FIRST 1(E) | |
| $ RFa | a $ | выброс | ||
| $ RF | $ | e | $Î FOLLOW 1(A) | |
| $ R | $ | e | $Î FOLLOW 1(A) | |
| $ | $ | успех |
 Левый разбор цепочки берем из столбца 3: 14862485863.
Левый разбор цепочки берем из столбца 3: 14862485863.
Пример2 для грамматики G0′. Вход: (+ a)* a.
| Стек | Вход | № правила | Правая часть | Комментарии |
| $ S | (+a)* a $ | TR | (Î FIRST 1(S) | |
| $ RT | (+a)* a $ | EF | (Î FIRST 1(T) | |
| $ RFE | (+a)* a $ | (S) | (Î FIRST 1(E) | |
| $ RF) S ( | (+a)* a $ | выброс | ||
| $ RF) S | + a)* a $ | ошибка | +Ï FIRST 1(S) |
4.5. Восходящий анализ (ведется, начиная от входной цепочки). (АУ-338?)
Говорят, что правовыводимую цепочку abw можно свернуть слева к aAw с помощью правила A ® b, если S Þr* aAw Þr abw Þr* xw. При этом b называют основой abw, а процедуру сверткой. Можно построить дерево редукций (см. пример восходящего разбора). Оно будет конечным. Построение дерева можно закончить, когда получим лист с начальным символом грамматики.
Не нашли, что искали? Воспользуйтесь поиском: