Схема проведения дисперсионного анализа

Источники вариации:	Вариация, объясненная за счет регрессии	Остаточная вариация	Общая вариация
Число степеней свободы
Сумма квадратов отклонений
Дисперсия на одну степень свободы
Фактическое значение критерия Фишера
Табличное значение критерия Фишера

(5.12)

(5.13)

. (5.14)

Критерий Фишера определяется следующим соотношением:

(5.15)

Использование критерия Фишера предполагает вычисление и его сравнение с табличным значением , которое зависит от уровня значимости и числа степеней свободы для факторной и остаточной сумм. определяется либо с помощью таблиц, либо с использованием специализированных пакетов программ, например, в Excel для этого может быть использована функция FРАСПРОБР().

Если , нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о справедливости гипотезы (о существенности этой связи, значимости уравнения регрессии). 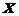Если же величина окажется меньше табличной, то есть , то вероятность нулевой гипотезы выше заданного уровня значимости (например, 0.05) и гипотеза не может быть отклонена без серьезного риска сделать неправильный вывод о наличии линейной связи между и 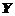. 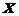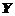В этом случае уравнение регрессии считается статистически незначимым, линейной связи между и нет.

Критерий Фишера может быть вычислен как по формуле (5.15), так и через коэффициент детерминированности по формуле:

(5.16)

где 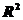- коэффициент детерминированности; - число наблюдений; - число параметров при переменных в рассматриваемом уравнении регрессии.

Проверка значимости параметров уравнения регрессии: коэффициентов уравнения регресси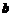и и и корреляции - проводится с помощью критерия Стьюдента.

С этой целью для каждого из параметров определяется стандартная ошибка (средняя квадратическая погрешность):

(5.17)

Статистики:

, (5.18)

имеют -распределение Стьюдента. Для заданного уровня значимости и соответствующего числа степеней свободы доверительные интервалы для параметров уравнения регрессии определяются по формулам:

; , (5.19)

где - табличное значение для заданного числа степеней свободы и уровня значимости. Значение 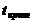можно получить с помощью функции Excel СТЬЮДРАСПОБР().

Выдвигается нулевая гипотеза о незначимом отличии коэффициента регрессии 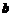в уравнении регрессии от нуля. По формулам (5.18) с учетом равенств (5.17) вычислим . Если вычисленное значение будет меньше критического, найденного для заданного уровня значимости и соответствующего числа степей свободы, то есть , то гипотеза о равенстве нулю коэффициента регрессии отклоняется. Аналогично проверяется значимость свободного члена в уравнении (5.4) и коэффициента корреляции.

В прогнозных расчетах предсказываемое значение 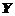определяется как точечный прогноз путем подстановки в уравнение регрессии 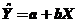значения . Однако, точечный прогноз маловероятен. Поэтому находят интервальную оценку прогноза:

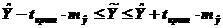, (5.20)

где - стандартная ошибка :

. (5.21)

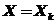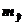Рассмотренная формула стандартной ошибки предсказываемого среднего значения при заданном значении характеризует ошибку положения линии регрессии. Чем больше разность между и , тем больше величина , это влечет увеличение доверительного интервала (рис.5.2.) На этом рисунке показано, что минимальная ширина доверительного интервала соответствует случаю, когда и совпадают. По мере удаления от на величины и ширина соответствующих доверительных интервалов увеличивается.

Рис. 5.2. Доверительный интервал линии регрессии:

U – верхняя граница; L – нижняя граница доверительного интервала; Δ₀, Δ₁,и Δ₂ доверительные интервалы для прогнозных значений равных , и соответственно.

Для сравнения качества различных моделей используется скорректированный индекс детерминации - , содержащий поправку на число степеней свободы:

. (5.22)

Другой оценкой качества уравнения регрессии является средняя ошибка аппроксимации - среднее отклонение теоретических значений от фактических, которая определяется по формуле:

. (5.23)

Модель считается пригодной для прогноза, если величина не превышает 8%-10%.

Для модели, описываемой уравнением (5.2) можно вычислить коэффициент эластичности. Коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %, и вычисляется по формуле:

, (5.24)

где - первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.

Для линейной модели

.

Не нашли, что искали? Воспользуйтесь поиском: