Вычисление определенного интеграла. Формула Ньютона-Лейбница.

Пусть в определенном интеграле нижний предел закреплен, а верхний предел меняется. Тогда будет меняться и значение интеграла, т.е. интеграл есть функция верхнего предела.
Для того чтобы иметь привычные обозначения, верхний предел обозначим через а чтобы не смешивать его с переменной интегрирования, последнюю обозначим через 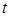. (От обозначения переменной интегрирования ззначение интеграла не зависит.) Получим интеграл . При постоянном этот интеграл будет представлять собой функцию верхнего предела . Эту функцию мы обозначим через

. (1)

Если -неотрицательная функция, то величина численно равна площади криволинейной трапеции (рис.220). Очевидно, что эта площадь изменяется в зависимости от изменения .

Найдем производную от по , т.е. найдем производную определенного интеграла (1) по верхнему пределу.

Теорема 1. Если -непрерывная функция и , то имеет место равенство

Иными словами, производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставленозначение верхнего предела (при условии, что подынтегральная функция непрерывна).

Доказательство. Дадим аргументу положительное или отрицательное приращение 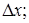тогда (учитывая свойство 6 определенного интеграла) получим Приращение функции равно т.е

К последнему интегралу применим теорему о среднем значении(свойство 5 определенного интеграла)

где 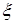заключено между и

Найдем отношение приращения функции к приращению аргумента:

Следовательно, Но так как при то а вследствие непрерывности функции

Таким образом, Теорема доказана.

Данная теорема просто иллюстрируется геометрически (рис.220): приращение 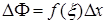равняется площади криволинейной трапеции с основанием 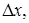а производная равна длине отрезка .

Замечание. Из доказанной теоремы, в частности, следует, что всякая непрерывная функция имеет первообразную. Действительно, если функция непрерывна на отрезке то, как указывалось в §2, в этом случаеопределенный интеграл 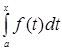существует, т.е. существует функция Но по доказанному выше она является первообразной от
Теорема 2. Если есть какая-либо первообразная от непрерывной функции то справедлива формула

(2)

Эта формула называется формулой Ньютона-Лейбница.

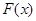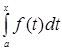Доказательство. Пусть есть некоторая первообразная от функции По теореме 1 функция есть также первообразная от А две любые первообразные от данной функции отличаются на постоянное слагаемое . Следовательно, можно написать

(3)

Это равенство при соответствующем справедливо при всех значениях , т.е. является тождеством. Для определения постоянного положим в этом тождестве 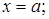тогда откуда

Следовательно,

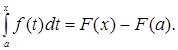
Полагая получим формулу Ньютона-Лейбница:

или, заменив обозначение переменной интегрирования на

Отметим, что разность не зависит от выбора первообразной так как все первообразные отличаются на постоянную величину, которая при вычитании все равно уничтожается.

Если ввести обозначение

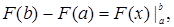
то формулу (2) можно переписать так:

Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известнапервообразная подынтегральной функции. Только с открытием этой формулы определенный интеграл смог получитьто значение в математике. Какое он имеет в настоящее время. Хотя с процессом, аналгичным вычислению определенного интеграла как предела интегральной суммы, были знакомы еще в древности, однако приложения этого метода ограничивались теми простейшими случаями, когда предел интегральной суммы мог быть вычислен непосредственно. Формула Ньютона-Лейбница значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различныых задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла к технике, механике, астрономии и т.д.

Не нашли, что искали? Воспользуйтесь поиском: