Законы Кирхгофа для мгновенных значений цепей изменяющегося тока 2 страница

Для определения числитель и знаменатель W(j ) разлагаются на множители не выше второго порядка

,

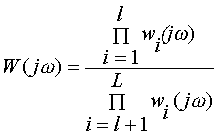тогда , где знак "+" относится к i=1,2,...,l (числителю передаточной фунции), знак "-" -к i=l+1,...,L (знаменателя передаточной функции).

Каждое из слагаемых определяется выражением

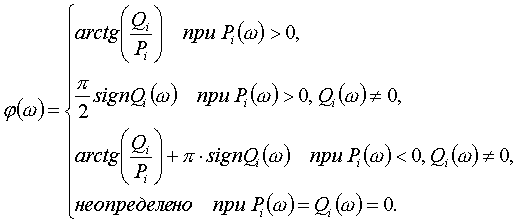
где .

Наряду с АФХ отдельно строят и все остальные частотные характеристики. Так АЧХ показывает, как пропускает звено сигнал различной частоты; причем оценкой пропускания является отношение амплитуд выходного и входного сигнала. ФЧХ показывает фазовые сдвиги, вносимые системой на различных частотах.

Помимо рассмотренных частотных характеристик в теории автоматического управления используются логарифмические частотные характеристики. Удобство работы с ними объясняется тем, что операции умножения и деления заменяются на операции сложения и вычитания. Построенная в логарифмическом масштабе АЧХ, называется логарифмической амплитудной частотной характеристикой (ЛАЧХ)

,

(2.43)

Эта величина выражается в децибелах (дб). При изображении ЛАЧХ удобнее по оси абсцисс откладывать частоту в логарифмическом масштабе, то есть , выраженную в декадах (дек).

Рис.2.7. Пример логарифмической амплитудной частотной характеристики

В логарифмическом масштабе может быть изображена также и ФЧХ:

Рис.2.8. Пример логарифмической фазовой частотной характеристики

Годограф кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала О

Понятие годографа было введено английским учёным У. Гамильтоном.

Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу. Например, скорость точки является величиной, изображаемой переменным вектором v. Отложив значения, которые имеет вектор v в разные моменты времени, от начала О, получим годограф скорости; при этом величина, характеризующая быстроту изменения скорости в точке М, то есть ускорение (в этой точке), имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке М’.

Пассивные двухполюсники и четырехполюсники включают набор резистивных и реактивных (индуктивных и емкостных) элементов, в которых протекают электрические токи под действием какого-либо одного внешнего источника энергии. Для описания физических явлений в таких цепях при воздействии на входных зажимах источника гармонических колебаний с фиксированной частотой =const используют метод комплексных амплитуд, который в свою очередь основывается на введении понятий комплексных сопротивлений или проводимостей отдельных элементов цепи - r, , , 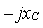а также комплексных амплитуд токов и напряжений – , [1].

В общем случае у источника гармонических колебаний может изменяться не только амплитуда и начальная фаза, но и угловая частота - . Тогда комплексная характеристика источника (входного воздействия) записывается в виде функции мнимой комплексной переменной - ( ). Эту характеристику обычно записывают в показательной (полярной) форме и называют комплексной спектральной плотностью. Модуль этой характеристики называют спектральной плотностью, а аргумент - фазовой плотностью или фазочастотной характеристикой. Так для напряжения имеем:

где - спектральная плотность напряжения, - фазовая плотность напряжения.

Аналогично гармонический ток с переменной угловой частотой ω характеризуется своей комплексной спектральной плотностью:

В зависимости от вида входного воздействия (электрического сигнала) спектральные плотности могут иметь непрерывный или дискретный характер. В дальнейшем для краткости будем опускать написание зависимости от угловой частоты, полагая , , , .

В реальном двухполюснике или четырехполюснике комплексные плотности токов и напряжений связаны между собой соотношениями, зависящими как от внутренних свойств элементов цепи, так и от способа соединения ветвей. Подобного рода соотношения называются частотными характеристиками.

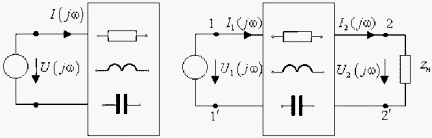
На рис.1.1а изображен двухполюсник, имеющий два входных зажима, к которым подсоединяется источник входного сигнала. Если к цепи присоединяется источник тока J (t), то входной ток i (t) = J (t), т.е. будет независимой функцией времени, а напряжение u (t) на входе определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение комплексов напряжения и тока.

(1.1)

Такое отношение называют комплексным входным сопротивлением

двухполюсника:

Из определения (1.1) следует, что Z (j ω) в свою очередь включает две характеристики: 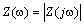- амплитудно-частотную характеристику (АЧХ) и 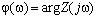- фазочастотную характеристику (ФЧХ) функции входного сопротивления.

а) б)

Рис. 1.1. Обобщенная комплексная схема замещения цепи:

а) двухполюсника; б) четырехполюсника

Если к цепи присоединяется источник напряжения e (t), то напряжение на двухполюснике u (t) = e (t), т.е. будет независимой функцией времени, a ток i (t) определится через свойства цепи как зависимая функция. При гармоническом характере входного сигнала определяют отношение тока к напряжению, которое называют комплексной входной проводимостью двухполюсника:

где Y (ω) и φ(ω) называют соответственно АЧХ и ФЧХ функции входной проводимости.

Функции Z (j ω) и Y (j ω) являются взаимно обратными функциями. В определении этих функций входят токи и напряжения, что дает возможность находить эти характеристики опытным путем, используя вольтметр, амперметр и прибор, измеряющий фазу гармонического колебания. Однако сами функции в силу линейности рассматриваемых цепей не зависят от величин токов и напряжений и могут быть определены непосредственно по структуре (топологии) цепи с учетом характера элементной базы ветвей. Для нахождения этих характеристик могут быть использованы все известные методы расчета цепей постоянного тока: законы Кирхгофа, простейшие преобразования, упрощающие схему и т.п. [1]. Исследование этих характеристик позволяет предсказать поведение цепи при различного рода воздействиях, о чем будет сказано далее.

Пример 1.1. Найти АЧХ и ФЧХ для функции входного сопротивления двухполюсника, образованного параллельным соединением резистивного и индуктивного элемента (рис.1.2а). Питание цепи осуществляется от источника синусоидального тока с любой частотой.

а) б)

Рис. 1.2. Схема для исследования входного сопротивления двухполюсника:

а) исходная схема; б) комплексная схема замещения

Решение задачи начинаем с построения комплексной схемы замещения исходной цепи (рис. 1.2б), на входе которой действует комплексный спектр источника тока I (j ω) = J (j ω), в результате чего на двухполюснике будет иметь место комплексный спектр напряжения U (j ω). Отношение их, определяемое выражением (1.1), может быть найдено непосредственно по структуре цепи путем объединения комплексных сопротивлений параллельно соединенных ветвей:

Сравнивая модули и аргументы, запишем АЧХ и ФЧХ

- АЧХ функции входного сопротивленияисследуемого выражения

φ(ω) = - ФЧХ функции входного сопротивления.

При построении графиков целесообразно перейти к относительной переменной Ω = ω L / r, которая указывает во сколько раз сопротивление индуктивности на данной частоте больше резистивного сопротивления. Для

этой переменной полученные выше выражения перепишутся в виде

Графики найденных функций представлены на рис.1.3а и рис.1.3б в относительных масштабных единицах.

а) б)

Рис. 1.3. Частотные характеристики функции входного сопротивления: а)АЧХ; б)ФЧХ

Расчетные значения сведены в таблице 1.

Таблица 1

		, Ом	, градусы	, градусы
	1.0
0.5	1.12	0.447 r	26.5	63.5
1.0	1.41	0.707 r	45.0	45.0
1.5	1.80	0.832 r	56.3	33.7
2.0	2.23	0.894 r	63.4	26.6
2.5	2.69	0.928 r	68.2	21.8
		r

Для перехода к реальной частоте необходимо знать численные значения параметров цепи r и L. Тогда переход осуществляется по формуле ω = r / L Ω (рад/с), если L измеряется в генри, а r в омах.

Из рассмотренного примера следует, что для нахождения аналитического выражения Z (j ω) или Y (j ω) как функции частоты следует задать входное напряжение U (или входной ток I) и найти входной ток I (или входное напряжение U), затем воспользоваться одним из выражений Z = U / I или Y = I / U.

Если известна структура и характер элементов цепи, то искомое выражение можно найти непосредственно, как это было сделано в примере 1.1. Полученное выражение обычно приводят к виду

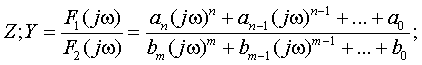
где и полиномы, зависящие от переменной . После преобразований с комплексными слагаемыми всегда есть возможность записать исследуемую функцию в полярной (показательной) форме, выделяя зависимости АЧХ и ФЧХ.

В простейших неразветвленных rL и rС цепях иногда используют понятие граничной частоты . Граничной называется частота, при которой r = X, т.е. = r / L, или = 1/ rС. Как следует из приведенного выше примера 1.1, на граничной частоте Z (ω) = 0.707 r, а φ(ω) = 45˚.

50. Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Свободные колебания в идеальном контуре – ДОДЕЛАТЬ111

Период, частота и длина волны свободных колебаний – ДОДЕЛАТЬ111

ХАРАКТЕРИСТИЧЕСКОЕ СОПРОТИВЛЕНИЕ КОНТУРА - отношение амплитуды напряжения на конденсаторе или равной ей амплитуды э.д.с. самоиндукции на катушке к амплитуде тока в колебательном контуре при последовательном резонансе. Также называют волновым сопротивлением контура.

Свободные колебания в реальном контуре – ДОДЕЛАТЬ111

ЗАТУХАНИЕ КОЛЕБАНИЙ - уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебат. системой. Потери энергии колебаний вызываются в механич. системах превращением её в теплоту вследствие трения и излучениемупругих волн в окружающую среду, в электрических системах - омич. потерями в них и излучением эл--магн. волн в окружающее пространство. Закон 3. к. определяется свойствами системы. В линейных системах 3. к. происходит по экспоненте:

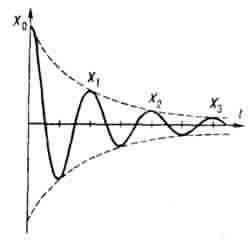
Х_к = Х₀ехр(-a t) (рис.), где t - время, a - показатель затухания системы. Для простейшей механич. системы -тела массы т, удерживаемого в положении равновесия упругой силой и испытывающего трение, пропорциональное скорости (с коэф. пропорциональности b), a=b/2m; для простейшей электрич. системы - колебательного контура с индуктивностью L и сопротивлением R a =R/2L. 3. к. практически можно считать закончившимся, если амплитуда колебаний уменьшилась до ~ 1% нач. величины. Время t, в течение к-рого это произойдёт, определяется из условия е ^-at = 0,01 или at=4,6, то есть t=4,6/a. К затухающим колебаниям, строго говоря, неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода T₁ как промежутка времени между двумя последующими максимумами колеблющейся величины (тока, напряжения, размаха колебаний маятника и т. д.). "Период" Т₁ увеличивается по мере увеличения потерь энергии в системе. Для приведённых выше простейших случаев соответствующая этому условному "периоду" частота затухающих колебаний где w₀ - угловая частота собств. колебаний в отсутствии потерь энергии в системе. Скорость 3. к. часто характеризуют декрементом затухания d=aT₁, определяющим уменьшение амплитуды за один "период" колебаний, или величиной d=d/p, наз. просто затуханием. Скорость 3. к. связана с добротностью колебат. системы Q; в рассмотренных простейших случаях d=l/Q. В нелинейных системах отношение потерь энергии за период к полной энергии колебаний не остаётся постоянным, а изменяется с изменением амплитуды колебаний. Поэтому закон 3. к. оказывается не экспоненциальным. Простейший с точки зрения закона 3. к. случай - это нелинейная механич. система, в к-рой величина силы трения постоянна (не зависит от величины скорости), а направление силы трения противоположно скорости (т. н. сухое трение). Такая сила трения возникает в системах, движение к-рых связано со скольжением, напр., при колебаниях крутильного маятника с осью, установленной в подшипниках скольжения. В этом случае амплитуды колебаний убывают по закону арифметич. прогрессии.

ДОБРОТНОСТЬ КОНТУРА – характеризует качество колебательного контура, обозначается Q. Численно равна отношению напряжения на любом из реактивных участков на резонансе к напряжению, подводимому к контуру, или отношению реактивного сопротивления к активному. При большой добротности контура напряжение на нем значительно превышает напряжение на входе контура.

51. Последовательный колебательный контур является простейшей резонансной (колебательной) цепью. Состоит последовательный колебательный контур, из последовательно включенных катушки индуктивности и конденсатора. При воздействии на такую цепь переменного (гармонического) напряжения, через катушку и конденсатор будет протекать переменный ток, величина которого вычисляется по закону Ома: I = U / Х_Σ, где Х_Σ - сумма реактивных сопротивлений последовательно включенных катушки и конденсатора (используется модуль суммы).
Для освежения памяти, вспомним как зависят реактивные сопротивления конденсатора и катушки индуктивности от частоты приложенного переменного напряжения. Для катушки индуктивности, эта зависимость будет иметь вид:

Из формулы видно, что при увеличении частоты, реактивное сопротивление катушки индуктивности увеличивается. Для конденсатора зависимость его реактивного сопротивления от частоты будет выглядеть следующим образом:

В отличии от индуктивности, у конденсатора всё происходит наоборот - при увеличении частоты, реактивное сопротивление уменьшается. На следующем рисунке графически представлены зависимости реактивных сопротивлений катушки X_L и конденсатора Х_C от циклической (круговой) частоты ω, а также график зависимости от частоты ω их алгебраической суммы Х_Σ. График, по сути, показывает зависимость от частоты общего реактивного сопротивления последовательного колебательного контура.
Из графика видно, что на некоторой частоте ω=ω_р, на которой реактивные сопротивления катушки и конденсатора равны по модулю (равны по значению, но противоположны по знаку), общее сопротивление цепи обращается в ноль. На этой частоте в цепи наблюдается максимум тока, который ограничен только омическими потерями в катушке индуктивности (т.е. активным сопротивлением провода обмотки катушки) и внутренним сопротивлением источника тока (генератора). Такую частоту, при которой наблюдается рассмотренное явление, называемое в физике резонансом, называют резонансной частотой или собственной частотой колебаний цепи. Также из графика видно, что на частотах, ниже частоты резонанса реактивное сопротивление последовательного колебательного контура носит емкостной характер, а на более высоких частотах - индуктивный. Что касается самой резонансной частоты, то она может быть вычислена при помощи формулы Томсона, которую мы можем вывести из формул реактивных сопротивлений катушки индуктивности и конденсатора, приравняв их реактивные сопротивления друг к другу:

На рисунке справа, изображена эквивалентная схема последовательного резонансного контура с учетом омических потерь R, подключенного к идеальному генератору гармонического напряжения с амплитудой U. Полное сопротивление (импеданс) такой цепи определяется: Z = √(R²+X_Σ²), где X_Σ = ω L-1/ωC. На резонансной частоте, когда величины реактивных сопротивлений катушки X_L = ωL и конденсатора Х_С= 1/ωС равны по модулю, величина X_Σ обращается в нуль (следовательно, сопротивление цепи чисто активное), а ток в цепи определятся отношением амплитуды напряжения генератора к сопротивлению омических потерь: I= U/R. При этом на катушке и на конденсаторе, в которых запасена реактивная электрическая энергия, падает одинаковое напряжение U_L = U_С = IX_L = IX_С.
На любой другой частоте, отличной от резонансной, напряжения на катушке и конденсаторе неодинаковы - они определяются амплитудой тока в цепи и величинами модулей реактивных сопротивлений X_L и X_С. Поэтому резонанс в последовательном колебательном контуре принято называть резонансом напряжений. Резонансной частотой контура называют такую частоту, на которой сопротивление контура имеет чисто активный (резистивный) характер. Условие резонанса - это равенство величин реактивных сопротивлений катушки индуктивности и ёмкости.

Одними из наиболее важных параметров колебательного контура (кроме, разумеется, резонансной частоты) являются его характеристическое (или волновое) сопротивление ρ и добротность контура Q. Характеристическим (волновым) сопротивлением контура ρ называется величина реактивного сопротивления емкости и индуктивности контура на резонансной частоте: ρ = Х_L = Х_C при ω =ω_р. Характеристическое сопротивление может быть вычислено следующим образом: ρ = √(L/C). Характеристическое сопротивление ρ является количественной мерой оценки энергии, запасенной реактивными элементами контура - катушкой (энергия магнитного поля) W_L = (LI²)/2 и конденсатором (энергия электрического поля) W_C=(CU²)/2. Отношение энергии, запасенной реактивными элементами контура, к энергии омических (резистивных) потерь за период принято называть добротностью Q контура, что в буквальном переводе с английского языка обозначает "качество". Добротность колебательного контура - характеристика, определяющая амплитуду и ширину АЧХ резонанса и показывающая, во сколько раз запасы энергии в контуре больше, чем потери энергии за один период колебаний. Добротность учитывает наличие активного сопротивления нагрузки R.
Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно, добротность вычисляется:

где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно. Величину, обратную добротности d = 1 / Q называют затуханием контура. Для определения добротности обычно пользуются формулой Q = ρ / R, где R -сопротивление омических потерь контура, характеризующее мощность резистивных (активных потерь) контура Р = I²R. Добротность реальных колебательных контуров, выполненных на дискретных катушках индуктивности и конденсаторах, составляет от нескольких единиц до сотни и более. Добротность различных колебательных систем, построенных на принципе пьезоэлектрических и других эффектов (например, кварцевые резонаторы) может достигать нескольких тысяч и более.

Частотные свойства различных цепей в технике принято оценивать с помощью амплитудно-частотных характеристик (АЧХ), при этом сами цепи рассматривают как четырёхполюсники. На рисунках ниже представлены два простейших четырехполюсника, содержащих последовательный колебательный контур и АЧХ этих цепей, которые приведены (показаны сплошными линями). По вертикальной оси графиков АЧХ отложена величина коэффициента передачи цепи по напряжению К, показывающая отношение выходного напряжения цепи к входному.

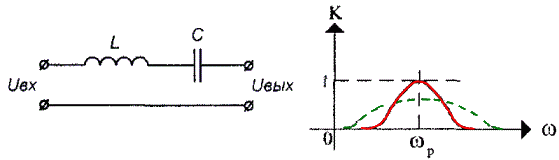
Для пассивных цепей (т.е. не содержащих усилительных элементов и источников энергии), величина К никогда не превышает единицу. Сопротивление переменному току изображённой на рисунке цепи, будет минимально при частоте воздействия, равной резонансной частоте контура. В этом случае коэффициент передачи цепи близок к единице (определяется омическими потерями в контуре). На частотах, сильно отличающихся от резонансной, сопротивление контура переменному току достаточно велико, а следовательно, и коэффициент передачи цепи будет падать практически до нуля.

При резонансе в этой цепи, источник входного сигнала оказывается фактически замкнутым накоротко малым сопротивлением контура, благодаря чему коэффициент передачи такой цепи на резонансной частоте падает практически до нуля (опять-таки в силу наличия конечного сопротивления потерь). Наоборот, при частотах входного воздействия, значительно отстоящих от резонансной, коэффициент передачи цепи оказывается близким к единице. Свойство колебательного контура в значительной степени изменять коэффициент передачи на частотах, близких к резонансной, широко используется на практике, когда требуется выделить сигнал с конкретной частотой из множества ненужных сигналов, расположенных на других частотах. Так, в любом радиоприемнике при помощи колебательных цепей обеспечивается настройка на частоту нужной радиостанции. Свойство колебательного контура выделять из множества частот одну принято называть селективностью или избирательностью. При этом интенсивность изменения коэффициента передачи цепи при отстройке частоты воздействия от резонанса принято оценивать при помощи параметра, называемого полосой пропускания. За полосу пропускания принимается диапазон частот, в пределах которого уменьшение (или увеличение - в зависимости от вида цепи) коэффициента передачи относительно его значения на резонансной частоте, не превышает величины 0,7 (3дБ).

Не нашли, что искали? Воспользуйтесь поиском: