ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Формула вычисления угла между прямой и плоскостью

⇐ Предыдущая 123 4 5 Следующая ⇒

Если в пространстве заданы направляющий вектор прямой L

s = {l; m; n}

и уравнение плоскости

Ax + By + Cz + D = 0,

то угол между этой прямой и плоскостью можно найти используя формулу

sin φ =	\| A · l + B · m + C · n \|
√A² + B² + C² · √l² + m² + n²

Пример 1.

Найти угол между прямой

x - 4	=	y + 2	= -	z - 6

и плоскостью x - 2y + 3z + 4 = 0.

Решение.

Из уравнения прямой найдем направляющий вектор прямой

s = {2; 6; -3}

Из уравнения плоскости найдем вектор нормали плоскости

q = {1; -2; 3}

Воспользовавшись формулой, найдем угол между прямой и плоскостью

sin φ =	\| 2 · 1 + 6 · (-2) + (-3) · 3 \|	=
√2² + 6² + (-3)² · √1² + (-2)² + 3²

sin φ =	\| 2 - 12 - 9 \|	=		=
√4 + 36 + 9 · √1 + 4 + 9	√49 · √14	7√14

Ответ:

sin φ =
7√14

18) § 1. Каноническое уравнение плоскости в пространстве

Пусть в декартовой системе координат дан вектор n ={A,B,C} и точка М₀=(x₀, y₀, z₀).

Построим плоскость Π, проходящую через т. М₀, перпендикулярную вектору n (этот вектор называют нормальным вектором или нормалью плоскости).

Утверждение 1: М Π  М₀М n.

М₀М={ x-x₀, y-y₀, z-z₀ } n  A(x-x₀)+B(y-y₀)+C(z-z₀)=0. (*)

(См. свойства скалярного произведения)

Каноническое уравнение плоскости в пространстве:

Аx+By+Cz+D=0, где D = -A x₀ -B y₀ -C z₀.

Пусть в декартовой системе координат дан вектор a ={p,q,r} и точка М₀=(x₀, y₀, z₀).

Построим прямую l, проходящую через т. М₀, параллельную вектору a (этот вектор называют направляющим вектором прямой).

Утверждение 2: М l  М₀М || a.

М₀М={ x-x₀, y-y₀, z-z₀ } || a  t R, т.ч. М₀М=t ·a =>

Параметрические уравнения прямой в пространстве:

(**)

Выразим из каждой строчки параметр t:

Канонические уравнения прямой в пространстве:

§3. Расстояние от точки до плоскости в пространстве

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М₁=(x₁,y₁,z₁).

Утверждение 3: расстояние от точки М₁ до плоскости Π вычисляется по формуле:

Если прямая проходит через точки (, ), (, ), то ее угловой коэффициент определяется по формуле

Признаком перпендикулярности двух прямых является соотношение

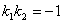, или .

Даны вершины треугольника . Требуется:

1) составить уравнения сторон и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить уравнение прямой 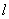, проходящей через точку 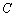параллельно прямой ;
5) составить уравнение высоты и найти её длину;
6) вычислить площадь треугольника ;
7) составить уравнение медианы ;
8) найти точку пересечения .

Составим уравнение стороны по точкам :

Таким образом, угловой коэффициент:

Аналогично находим уравнения сторон . Не вижу особого смысла расписывать то же самое, поэтому сразу приведу готовый результат:

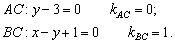
2) Найдём длину стороны Для точек используем формулу:

3) Найдём . Это угол при вершине . Используем формулу .

Найдём векторы:

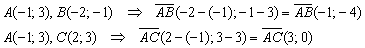
Таким образом:

В результате:

Эллипс – геометрическое место точек на плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

В прямоугольной декартовой системе координат уравнение эллипса записывается следующим образом:

Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности.

Если эксцентриситет равен 1, то кривая--парабола.
Если больше чем 1, то кривая -- гипербола. Для гиперболы эксцентриситет считается по той же формуле, что и для эллипса e=c/a.
Для всех трех кривых есть единое уравнение в полярных координатах, куда входит эксцентриситет:
r = p/(1-e cos фи), здесь p -- параметр кривой, то есть половина хорды, проведенной через фокус перпендикулярно оси.

Каноническое уравнение эллипса -Введём декартову систему координат с центром в средней точке между фокусами эллипса. Пусть координаты фокусов будут (-c;0), (c;0).
Тогда расстояние от переменной точки (x;y) эллипса до левого фокуса
r1=sqrt((x+c)^2+y^2), а до правого r2=sqrt((x-c)^2+y^2).

Уравнение эллипса: r1+r2=2a.
Переносим r1 вправо, возводим в квадрат и так далее.
По пути вводится обозначение b^2=a^2-c^2.

Построить эллипс, заданный уравнением

Решение: сначала приведём уравнение к каноническому виду:

В данном случае

20

Гипербола- множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности.

Если эксцентриситет равен 1, то кривая--парабола.
Если больше чем 1, то кривая -- гипербола. Для гиперболы эксцентриситет считается по той же формуле, что и для эллипса e=c/a.
Для всех трех кривых есть единое уравнение в полярных координатах, куда входит эксцентриситет:
r = p/(1-e cos фи), здесь p -- параметр кривой, то есть половина хорды, проведенной через фокус перпендикулярно оси.

21 Парабола- геометрическое место точек, равноудалённых от данной прямой(называемой директрисой параболы) и данной точки (называемой фокусом параболы). Пусть r-расстояние от точки параболы до фокуса.d-расстояние от точки параболы до директрисы. Тогда,по определению уравнение параболы равно r=d. Получим уравнение параболы, расположенной в плоскости с д.п.с.к. X0Y. Пусть фокус F принадлежит оси 0X. Директрису проведем перпендикулярно оси 0Х на расстоянии p от фокуса F. Пусть начало координат т. 0 – является серединой этого расстояния. Пусть т. M(x;y) – «текущая» точка параболы. Пусть r-расстояние от т.М (x;y) до директрисы По определению параболы r=d. По теореме Пифагора из прямоугольного Δ F MN: Расстояние от точки М(x;y)до директрисы , .Таким образом Возведя обе части в квадрат, получим откуда -каноническое уравнение параболы Пример построения параболы Построим параболу y=4x Решение: вершина известна, найдём дополнительные точки. Уравнение y= =2 . - определяет верхнюю дугу параболы, уравнение y= -2 -нижнюю дугу параболы. В целях сократить запись вычисления проведём y= В моем примере F(1;0) d: x+1=0

22 Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Декартовой системой координат в пространстве называется совокупность точки и базиса. Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке. Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и  формулами x = ρcos  y = ρsin . Полярные координаты ρ и  точки М выражаются через ее декартовые координаты и формулами ρ= + (Синус наоборот Y) Замечание. Если не указано положение полюса и полярной оси относительно декартовой системы координат, то считаем, что полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс. Уравнение прямой в полярной системе координат - Если задать расстояние р от полюса О и угол Альфа между полярной осью и осью L, проходящей через полюс к данной прямой.Очевидно все точки данной прямой линии и только они обладают следующим свойством:проекция на ось L отрезка ОМ,проведенного из полюса О в точку М прямой линии равна p. Обозначая через r и Ф координаты произвольной точки прямой линии,указанное свойство мы можем записать в виде r cos(Ф-a)=р Это и есть уравнение прямой. Уравнение окружности в полярной системе координат В полярной системе координат вывести уравнение окружности, которая имеет центр С(p0; 0) и радиусом r Обозначим буквой М произвольную точку окружности, буквами P и ее полярные координаты. Так как точка М может занимать на окружности любое положение, то P и являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами. Все точки окружности отстоят от центра на расстоянии r; запишем это условие символически: (1) Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов) Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты P и точки М можно упростить

23 Кардио́ида — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Уравнение Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами. Архимедова спираль — спираль, плоская кривая, траектория точки M (см Рис. 1), которая равномерно движется вдоль луча OV с началом в O, в то время как сам луч OV равномерно вращается вокруг O где k — смещение точки M по лучу r, при повороте на угол равный одному радиану. Логарифми́ческая спира́ль или изогональная спираль — особый вид спирали, часто встречающийся в природе. или где — угол отклонения точки от нуля, r — радиус-вектор точки, a — коэффициент, отвечающий за расстояние между витками, b — коэффициент, отвечающий за густоту витков. Гиперболическая спираль — плоская трансцендентная кривая.

Каноническое уравнениегиперболы имеет вид где a и b –положительные действительные числа. В отличие от эллипса здесь не накладывается условие a>b.то есть, значение а может быть и меньше значения бэ.

Построение гиперболы по каноническому уравнению

Обозначим фокусы через F₁ и F₂ расстояние между ними через 2с, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2a. По определению 2a < 2с, т. е. a < c.. Для вывода уравнения гиперболы выберем систему координат Ox1 так, чтобы фокусы F₁ и F₂ лежали на оси Oy а начало координат совпало с серединой отрезка F₁F₂. Тогда фокусы будут иметь координаты F1(c;0) F2(-c;0).Пусть М(x;y)-произвольная точка гиперболы.Тогда согласно определению гиперболы или MF1-MF2=+2 т.е.

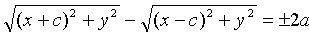
После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы

Гипербола есть линия второго порядка.

24 Кривая второго порядка — геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов

отличен от нуля Невырожденные кривые(эллипс, гипербола, парабола)если дельта неравно 0 Вырожденные кривые (вырожденная парабола, вырожденная гипербола)если дельта равно 0 Характеристика линий –кордиода и т.д.

25 1) Область определения функции и область значений функции. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции - это множество всех действительных значений y, которые принимает функция. В элементарной математике изучаются функции только на множестве действительных чисел. 2) Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю. 3) Промежутки знакопостоянства функции. Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны. 4) Монотонность функции. Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции. Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции. 5) Четность (нечетность) функции. Четная функция - функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат. Нечетная функция - функция, у которой область определения симметрична относительно начала координат и для любого из области определения справедливо равенство f(-x) = - f(x). График нечетной функции симметричен относительно начала координат. 6) Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x. Если такого числа не существует, то функция - неограниченная. 7) Периодичность функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы). Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.

Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность)

Парабола - график функции квадратного трёхчлена у = ах²+ bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax²+ bx +с =0

Гипербола - график функции Y=

. При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).

Экспонента (показательная функция по основанию е) у = е^x. (Другое написание у = ехр(х)). Асимптота - ось абсцисс.

у = sinx. Синусоида - периодическая функция с периодом Т = 2π

Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на пи на два)

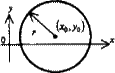Окружность с центром в точке (x_o, y_o) радиуса r. (x-x_o)²+ (y-y_o)²= r²

Эллипсс центром в точке (x_o, y_o). Большая полуось а, малая b, эксцинтриситет

27 .ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ Числовой последовательностью (или просто последовательностью) называется функция

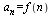, определенная на множестве всех натуральных чисел 1, 2,..., n,.... Значения последовательности

называются ее членами. Последовательность

иногда обозначают так:

. Это означает, что задана последовательность с общим членом

. По данному общему члену всегда можно найти любой член последовательности

, подставив в

вместо n число k. Для последовательности, как и для любой функции, можно построить график. Он не является линией, а состоит из отдельных точек, расположенных справа от оси Оу. На рис. изображен график последовательности

; он состоит из следующих точек: (1; -1), (2; 2), (3; -3), (4; 4),....

Последовательность

называется невозрастающей (неубывающей), если для любого номера n справедливо неравенство

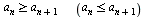. Если

, то последовательность

— убывающая (возрастающая). Последовательности всех этих типов носят общее название — монотонные. Убывающие и возрастающие последовательности называются строго монотонными, невозрастающие и неубывающие — монотонными в широком смысле. Последовательность

называется ограниченной сверху (снизу), если существует такое число М, что для любого номера n выполняется неравенство

(соответственно

). Последовательности, ограниченные одновременно сверху и снизу, называются ограниченными. Число а называется пределом последовательности

, если для любого числа ε > 0 существует такой номер N = N (ε), зависящий от ε, что для всех n > N выполняется неравенство

Это обозначают так:

или

. Пример. Докажем, что

. Пусть ε > 0 — произвольное число. Тогда

Из последнего неравенства следует, что в качестве номера N можно взять целую часть числа

, т. е.

Итак,

28 ТЕОРЕМЫ О ПРЕДЕЛАХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 1. Последовательность, имеющая предел, ограничена. 2. Последовательность может иметь только один предел. 3. Любая неубывающая (невозрастающая) и ограниченная сверху (снизу) последовательность имеет предел. 4. Предел постоянной равен этой постоянной:

5. Предел суммы равен сумме пределов:

6. Постоянный множитель можно выносить за знак предела:

7. Предел произведения равен произведению пределов:

. 8. Предел частного равен частному пределов, если предел делителя отличен от нуля:

9. Если

и обе последовательности

имеют один и тот же предел а, то

В теоремах 5—8 предполагается, что все пределы в правой части равенств существуют!!! Пример. Найдем предел

. Имеем

Предел последовательности – это число, в окрестности которой содержатся все члены последовательности. Пример: Пределом последовательности чисел 1/2, 1/3, 1/4, 1/5, 1/6 и т.д. является 0. Пояснение: ряд чисел стремится к нулю и ниже нуля не опустится. Не любая последовательность имеет предел. К примеру, последовательность 1, 2, 3, 4, 5, 6 и т.д. бесконечна и не имеет предела. Свойство последовательности иметь или не иметь предел называется сходимостью. Если у последовательности есть предел, то говорят, что она сходится. Если у последовательности нет предела, то говорят, что она расходится. Пример 1: Найти предел последовательности d_n = 6/n – 4/n² + 8. Решение: lim 6/n – lim 4/n² + lim 8 = 0 – 0 + 8 = 8. ^n→∞^n→∞^n→∞ Пример решен. Пример 2: Найти предел последовательности 2n² + 3 lim ———— ^n→∞ n² + 4 Решение. Разделим числитель и знаменатель дроби на n², произведем сокращения и получим ответ: 2n²/n² + 3/n² 2 + 3/n² 2 + 0 lim ——————— = lim ————— = ———— = 2. ^n→∞ n²/n² + 4/n² ^n→∞ 1 + 4/n² 1 + 0 Пример решен. 29 Число A называется пределом функцииf (x) при x → x ₀ (или в точке x ₀), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < | x − x ₀| < δ, справедливо неравенство | f (x) − A | < ε, т.е. lim(x → x ₀) f(x) = A Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Геометрический смысл - Число А₁ называется пределом функции у=ƒ(х) слева в точке х_о, если для любого число ε>0 существует число δ=δ(ε)> 0 такое, что при х є (х₀-δ;x_o), выполняется неравенство |ƒ(х)-А|<ε. Предел слева записывают так: limƒ(х)=А при х–>х₀-0 или коротко:ƒ(х_о0)=А₁ (обозначение Дирихле)

30 Число b называется пределом функции y=F(x) на бесконечности или при

,если для любого

существует число

такое, что для всех

из того, что

выполняется неравенство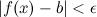

Алгебраические свойства приделов в билете 28 Бесконечно малая — числовая функция или последовательность, которая стремится к нулю. Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Функция называется бесконечно малой в окрестности точки X0, если Функция называется бесконечно малой на бесконечности, если Функция называется бесконечно большой в окрестности точки X0, если 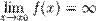Функция называется бесконечно большой на бесконечности, если

31 Алгебраические свойства пределов(док-во) Теорема 1:Если функция имеет положительный предел при, то она положительна в некоторой окрестности. Доказательство: Пусть. Возьмём в качестве. Тогда на основании определения предела имеем:. Т.е.. Аналогично доказывается для отрицательного значения предела. Теорема 2:Если функция неотрицательна в некоторой окрестности и имеет предел в этой точке, то этот предел также неотрицательный, т.е. если, тогда Доказательство: От противного: П., тогда по Т1: такая, что:, что противоречит условию.

33.

Определение

Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.

⇐ Предыдущая 123 4 5 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском:

vikidalka.ru - 2015-2025 год. Все права принадлежат их авторам! Нарушение авторских прав | Нарушение персональных данных