ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Дифференциальные уравнения, интегрируемые в квадратурах
ЛЕКЦИЯ 6
Раздел VI
Дифференциальные уравнения
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-ГО ПОРЯДКА
Основные понятия
Обыкновенным дифференциальным уравнением1-го порядка называют уравнение, в которое неизвестная функция одной переменной входит под знаком производной или дифференциала. Решение дифференциального уравнения 1-го порядка – это дифференцируемая на некотором промежутке функция, которая при подстановке в уравнение обращает его в верное равенство в каждой точке промежутка.
Если дифференциальное уравнение 1-го порядка записано в виде
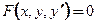, (1)
то оно называется не разрешенным относительно производной. Здесь: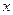 
− независимая переменная, 
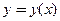− искомая функция, F − заданная функция трех переменных.
Уравнение
...... 
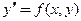(2)
называют дифференциальным уравнением 1-го порядка, разрешенным относительно производной.
Запись дифференциального уравнения 1-го порядка в виде
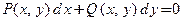(3)
называют дифференциальной формой (записи) дифференциального уравнения 1-го порядка, а само уравнение − уравнением в дифференциалах. Это уравнение симметрично относительно переменных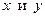 
: его решениями могут быть и функции переменной х: 
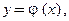и функции переменной у: 
.
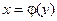Кроме обыкновенных дифференциальных уравнений в науке рассматривают уравнения в частных производных, в которых неизвестная функция зависит от нескольких, как минимум от двух, независимых переменных. Например, уравнение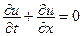 
является дифференциальным уравнением в частных производных первого порядка. Уравнения в частных производных широко применяются в механике сплошных сред, теории теплопроводности, квантовой физике и других областях знания. Поскольку в этом разделе рассматриваются только обыкновенные дифференциальные уравнения, то термин «обыкновенные», как правило, писать не будем.
Примером дифференциального уравнения 1-го порядка является уравнение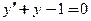 
. Это уравнение записано в виде (1), не разрешенном относительно производной. Если изменить запись, переписав его в виде 
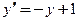, то получим дифференциальное уравнение вида (2), разрешенное относительно производной. Если представить производную как отношение двух дифференциалов, т.е.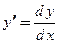 
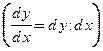и умножить обе части уравнения на дифференциал 
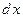, то получим уравнение в дифференциалах вида (3):
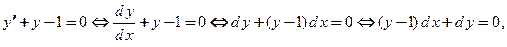
где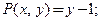 
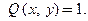
Решение дифференциального уравнения может быть записано разными способами. Наряду с явным представлением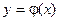 
решение дифференциального уравнения может быть записано и в параметрическом виде соотношениями: 
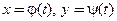. Для проверки, является ли параметрически заданная функция решением, нужно подставить производную 
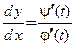, и переменные 
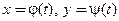в уравнение и выяснить, имеет ли место равенство при значениях параметра 
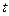, заполняющих некоторый промежуток. Решение, записанное в неявном виде 
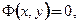называют интегралом уравнения. В этом случае при проверке нужно найти дифференциал интеграла 
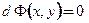и показать, что полученное выражение равносильно заданному дифференциальному уравнению на некотором промежутке числовой оси.
Процесс решения дифференциального уравнения называют интегрированием уравнения, причем этот термин используют даже тогда, когда не прибегают к нахождению интегралов. График решения называется интегральной кривой.
Дифференциальное уравнение 1-го порядка называют автономным, если в этом уравнении отсутствуют в явном виде сама независимая переменная x. Например, уравнения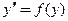 
, 
являются автономными. Стационарным решением произвольного дифференциального уравнения называют постоянные решения вида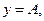 
где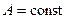 
. Для автономного уравнения 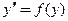стационарными решениями являются функции 
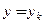, где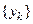 
− множество корней уравнения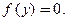 
Теорема 1 (о существовании и единственности решения задачи Коши). Если функция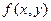 
непрерывна в области 
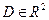и имеет ограниченную частную производную 
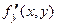в области 
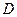, то для любой точки 
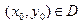в некоторой окрестности 
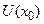точки 
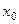существует единственное решение 
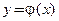задачи Коши:
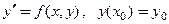. (4)
Уравнение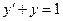 
из примера 1 можно переписать в виде: 
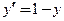. Обозначим правую часть 
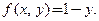Функция 
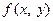− элементарная и, следовательно, непрерывная во всей плоскости 
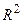. Эта функция имеет конечную частную производную 
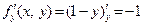в любой точке плоскости. По теореме 1 задача Коши для этого уравнения при любых начальных условиях имеет и притом единственное решение.
Общее решение дифференциального уравнения 1-го порядка в области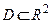 
– это функция 
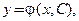обладающая следующими свойствами:
1) она является решением дифференциального уравнения при любых допустимых значениях постоянной (константы)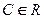 
;
2) для любой точки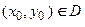 
найдется такое значение константы 
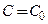, что 
является решением задачи Коши для рассматриваемого дифференциального уравнения с начальным условием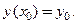 
Общий интеграл − это общее решение, записанное в неявном виде: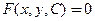 
. Общее решение дифференциального уравнения 1-го порядка задает в области 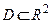однопараметрическое семейство интегральных кривых. Решение, полученное из общего решения при конкретном значении параметра С, называют частным решением.
Ранее было доказано, что функция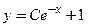 
является решением дифференциального уравнения 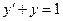при любых значениях 
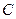. Чтобы функция 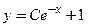была общим решением этого уравнения, осталось доказать, что для любой точки 
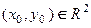найдется такое значение 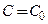, что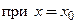 
справедливо 
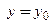. Вычислим значение функции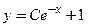 
: 
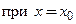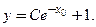Составим уравнение для определения 
: 
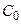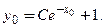Решим его: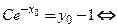 
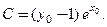Обозначим это значение параметра 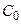. Как видим, для любой точки 
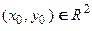существует и притом единственное значение параметра 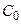. Согласно определениям, 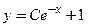является общим решением уравнения 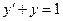; функция 
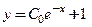, или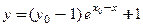 
− частным решением (на всей числовой оси).
Дифференциальные уравнения, интегрируемые в квадратурах
Самое простое дифференциальное уравнение 1-го порядка имеет вид: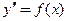 
, где 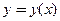− искомая функция, 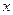− независимая переменная, 
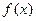− заданная непрерывная на некотором промежутке функция. Отыскание решения этого уравнения представляет собой классическую задачу математического анализа − задачу отыскания (восстановления) функции по ее производной, которая успешно решается при помощи интегрирования: 
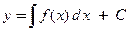, где С − произвольная постоянная. В этом случае говорят, что решение записано в квадратурах. Так, например, для определения пути 
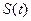, пройденного материальной точкой при прямолинейном поступательном движении со скоростью 
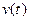, нужно решить уравнение 
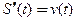. Проинтегрировав, получим решение в квадратурах: 
.
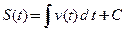В этом разделе рассмотрены дифференциальные уравнения 1-го порядка нескольких типов, для которых указаны названия, характерные признаки и методы решения. Эти уравнения объединяет возможность тем или иным приемом перейти к уравнению или системе двух уравнений с разделяющимися переменными, т.е. к уравнениям, в которых переменные могут быть разделены путем преобразований. Ниже приведен краткий обзор методов решения уравнений, собранных в табл. 1. После обзора и таблицы на примерах продемонстрированы описанные методы. Наиболее полное собрание уравнений, интегрируемых в квадратурах, представлено в справочнике [25].
1. Уравнения с разделенными переменными. Наиболее общий вид уравнений, который можно непосредственно интегрировать, − это уравнения с разделенными переменными: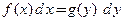 
(п. 1 табл.1).Общий интеграл уравнения 
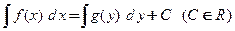записан в квадратурах.
2. Уравнения с разделяющимися переменными. Любое дифференциальное уравнение, тождественными преобразованиями приводящееся к уравнению с разделенными переменными, называют уравнением с разделяющимися переменными. Частным случаем уравнения с разделяющимися переменными является уравнение в дифференциалах вида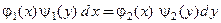 
(п.2 табл.1).Если 
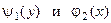отличны от нуля, то после деления обеих частей уравнения на произведение этих функций получаем уравнение с разделенными переменными 
, которое можно интегрировать. Если уравнения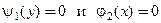 
имеют корни 
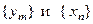, принадлежащие области определения дифференциального уравнения, то функции 
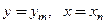также являются решениями исходного дифференциального уравнения.
3. Однородные уравнения. Однородные уравнения допускают две формы записи.
Первая форма записи. Если дифференциальное уравнение, разрешенное относительно производной, имеет вид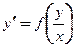 
, то это уравнение называют однородным. При помощи подстановки 
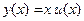оно приводится к уравнению с разделяющимися переменными: 
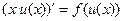, или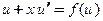 
. Отсюда 
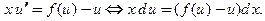Далее разделяем переменные и интегрируем: 
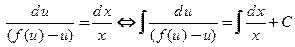, после чего выполняем обратную замену. Если уравнение 
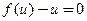имеет решения 
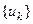, то функциями 
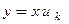нужно пополнить множество решений дифференциального уравнения.
Вторая форма записи. Если в уравнении в дифференциалах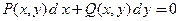 
функции 
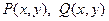являются однородными функциями одинаковой степени, то это уравнение также называют однородным и решают подстановкой 
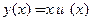(см. процедуру решения для первой формы записи). Заметим, что от одной формы записи однородного уравнения всегда можно перейти к другой.
4. Линейные уравнения. Уравнение вида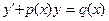 
называют линейным неоднородным уравнением относительно функции 
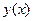, если 
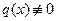. Как указано в п. 4 табл. 1, построение решения неоднородного уравнения выполняется последовательным решением двух уравнений с разделяющимися переменными.
В методе Лагранжа (методе вариации произвольной постоянной) сначала решают уравнение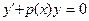 
. Это вспомогательное уравнение получают заменой правой части уравнения нулем и называют соответствующим линейным однородным уравнением. Это уравнение является уравнением с разделяющимися переменными: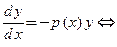 
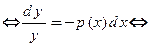
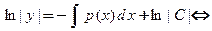
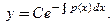Введем функцию 
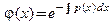. Тогда 
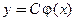− общее решение однородного уравнения. Теперь приступим к варьированию (изменению) произвольной постоянной С. Представим решение неоднородного уравнения в виде, формально совпадающем с видом общего решения однородного уравнения 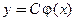, но будем полагать, что 
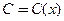− это неизвестная функция. Подставим 
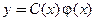в неоднородное уравнение и получим относительно 
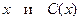уравнение с разделяющимися переменными:
,
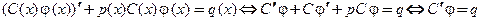так как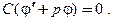 
Из уравнения 
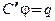находим производную 
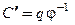, откуда 
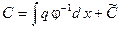, или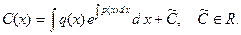 
Запишем ответ: 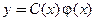, или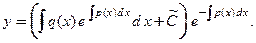 
Метод Бернулли называют также методом подстановки. Решение линейного неоднородного уравнения представляют, как и в методе Лагранжа, в виде произведения двух функций: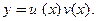 
Как видим, прослеживается аналогия с методом Лагранжа, но идея, реализуемая при применении метода Бернулли, иная. Подставим произведение 
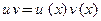в исходное неоднородное уравнение и перегруппируем слагаемые: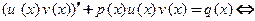 
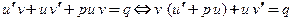. Выберем множитель 
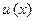таким образом, чтобы уравнение относительно второго множителя 
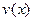приняло наиболее простой вид. Если 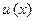− конкретное нетривиальное решение 
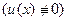уравнения 
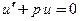, то функция 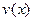должна быть общим решением уравнения: 
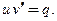Тогда общее решение неоднородного уравнения − это произведение функций 
.
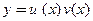5. Уравнение Бернулли − это нелинейное уравнение вида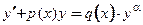 
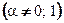. Для его решения применимы методы Лагранжа и Бернулли. Так, например, система для отыскания множителей 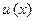, 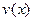в решении 
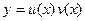, получаемом методом Бернулли, имеет вид: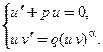 
При помощи подстановки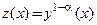 
нелинейное уравнение Бернулли сводится к линейному неоднородному уравнению, которое далее следует решать методом Лагранжа или Бернулли, после чего нужно выполнить обратную замену. Как правило, целесообразно сразу применить метод Лагранжа или Бернулли, минуя замену переменной.
6. Уравнение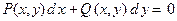 
называют уравнением в полных дифференциалах, если его левая часть является полным дифференциалом 
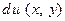некоторой функции двух переменных. Чтобы уравнение было уравнением в полных дифференциалах необходимо и достаточно, чтобы в некоторой односвязной области D существовали непрерывные частные производные 
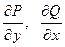, удовлетворяющие условию 
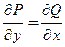. Тогда заданное уравнение принимает вид 
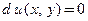, а его решение 
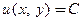, где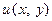 
следует найти из системы:
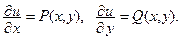
Уравнения интегрируются последовательно. Сначала из первого уравнения при 
интегрированием находят функцию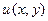 
с точностью до произвольного слагаемого 
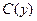, затем после подстановки 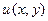во второе уравнение интегрированием находят 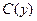и составляют ответ. Если в системе более простым является второе уравнение, то начинают решение со второго уравнения, полагая 
.
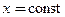Не нашли, что искали? Воспользуйтесь поиском: