ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вписати правильний 10-кутник в дане коло.
Розв’язання. Будуємо точку F (рис. А. 19), як і в п. 9 ОF є сторона шуканої фігури. Розхилом циркуля, який дорівнює ОF, зробимо на колі десять послідовних засічок. Отримаємо вершини даної фігури. Правильні багатокутники, вписані в коло, які мають сім і дев’ять сторін, не можуть бути точно побудовані тільки за допомогою циркуля і лінійки.
20.Довкола даного кола описати правильний трикутник, п’ятикутник, шестикутник, восьмикутник, десятикутник.
Розв’язання. Відмітимо на колі (рис. А. 22) вершини А, В, …, F правильного вписаного багатокутника з тим же числом сторін. Проведемо радіуси ОА, ОВ, …, ОF і продовжимо їх. Дугу АВ розділимо навпіл точкою Е. Через Е проведемо JP⊥OE. Відрізок JP, розміщений між продовженнями сусідніх радіусів, є сторона шуканої фігури. На продовженні інших радіусів відкладаємо відрізки OK, OL, …, ON, що дорівнюють ОР. Точки J, K, L, …, N, P послідовно з’єднуємо. Багатокутник JKLM … NP – шуканий [8, с. 74].
РОЗДІЛ 2 ПРАКТИЧНИЙ АНАЛІЗ ЗАСТОСУВАННЯ ЗАДАЧІ АПОЛЛОНІЯ
2.1 Частинні випадки задачі Аполлонія.
Задача Аполлонія полягає в тому, щоб побудувати за допомогою циркуля і лінійки коло, що дотикається до трьох даних кіл. Задача розв’язується за допомогою застосування двох операцій: інверсії і переходу до концентричних кіл. За легендою, задача сформульована Аполлонієм Пергським приблизно в 220 р. до н.е. в книзі «Дотик» під псевдонімом Епафай, яка була втрачена, але була відновлена в 1600 р. Франсуа Вієтом, «гальським Аполлонієм», як його називали сучасники. Робота була згадана Паппом Олександрійським в 4-му столітті. Спосіб, за допомогою якого розв’язав цю задачу Аполлоній, невідомо. Багато задач у складі аналізованих в шкільному курсі геометрії представляють частинні або похідні випадки задачі Аполлонія. Частинні випадки виникають при спеціальній розстановці даних кіл, похідні – коли всі чи деякі із даних кіл переходять в точки (радіус кола необмежено зменшується) або прямі (радіус необмежено збільшується).Перш ніж розв’язати задачу Аполлонія в загальному випадку, розглянемо деякі частинні її випадки. Задача 2.1.1. Побудувати за допомогою циркуля і лінійки коло, що дотикається до трьох точок. Розв’язання: З'єднаємо ці точки. Проведемо до знайдених відрізків серединні перпендикуляри. Вони перетнуться в одній точці. Ця точка - центр шуканого кола (рис. Б. 1). Задача 2.1.2. Побудувати за допомогою циркуля і лінійки коло, що дотикається до 2 точок і кола. Розв’язання: Проведемо через А і В довільне коло
, що перетинає 
в точках C і D, і позначимо через P точку перетину прямих AB і CD. Далі проведемо через Р дотичну до даного кола і позначимо через X точку дотику. Тоді коло 
, що проходить через A, B і X, буде шуканим (рис. Б. 2). Задача 2.1.3. Побудувати за допомогою циркуля і лінійки коло, що дотикається до 2 прямих и кола. Розв’язання: Якщо прямі паралельні, то радіус шуканого кола дорівнює половині відстані між ними, і її центр легко будується. Припустимо, що дані прямі а і в перетинаються в точці P, і позначимо через К невідому точку дотику даного кола 
і шуканого кола . Коло переходить в при деякій гомотетії з центром К. Ця гомотетія переводить пряму, що стосується , в паралельну їй пряму 
, яка дотикатиметься . Пряму легко побудувати Так само будується і образ 
. А точка Q перетину і - це образ точки P при тій же гомотетії. Але будь-яка точка, її образ при гомотетії і центр гомотетії лежить на одній прямій. Значить, точка К лежить на перетині прямої PQ з даним колом (рис. Б. 3). Тепер задача звелася до побудови кола, що стосується даних прямих і проходить через дану точку К. Оскільки кожну з дотичних і можна провести двома способами, а пряма PQ може мати до двох точок перетину з даним колом, завдання може мати до восьми рішень. Задача 2.1.4. Побудувати за допомогою циркуля і лінійки коло, що дотикається до точки, прямої і кола. Розв’язання: Нехай А, а, 
- дані точка, пряма і коло, – шукане коло, К і L - точки її дотику з , і а, відповідно. При гомотетії з центром К, що переводить в , пряма перейде в паралельну їй дотичну до . Тому точка L перейде в таку точку M кола , що виходить з неї діаметр перпендикулярний К. Позначимо другий кінець цього діаметра через B, а точку, в якій він при продовженні перетинає, через С. Нехай X - точка перетину прямої AM з колом . Точки В, С, L і К лежать на деякому колі, так як кут BCL = 90 ° і кут BKL = ВКМ = 90 °. Тому MC • MB = МК • ML. Точки X, A, L і K лежать на одному колі з побудови, так що MK • ML = MX • MA. Тому точку X можна побудувати із співвідношення MX • MA = MC • МВ, в якому нам вже відомі всі точки, крім X. Найпростіше це зробити, провівши ще одне коло - через А, В і С, Х - це точка її перетину з МА. Тепер залишається провести коло, що стосується а, через дві відомі точки А і X, а цю задачу ми вже вміємо розв’язувати (рис. Б. 4). Оскільки вона має, два рішення, а в якості точки М в нашій побудові можна взяти будь-який з двох кінців діаметру, найбільше число рішень в даному випадку дорівнює чотирьом. Задача 2.1.5. Побудувати за допомогою циркуля і лінійки коло, що дотикається до точки та 2 кіл. Розв’язання: Нехай потрібно побудувати коло, що проходить через дану точку A, щодо існування двох даних кіл і зовнішнім чином. Нехай 
і 
- точки дотику. Скористаємося тим, що вони лежать на одній прямій із зовнішнім центром подібності Z даних кіл. (Довести це можна за допомогою теореми Менелая для трикутника OO 1 O 2, (На сторону 
і 
взято відповідно точки і , а на продовженні сторони 
- точку Z. Для того, щоб точки і , Z лежали на одній прямій необхідно і достатньо щоб виконувалась рівність) 
, де R 1, R 2 и R - радіуси відповідних кіл; рівність останніх множників в похідних випливає з того, що Z - центр гомотетії з коефіцієнтом R 2: R 1, що переводить O 1 в O 2). По теоремі про ступінь точки звідси випливає, що шукане коло проходить через таку точку X прямою ZA, що ZX · ZA = ZK 1· ZK 2. Якщо ми знайдемо добуток в правій частині цієї рівності, то знайдемо і точку X, і тоді завдання зведеться до побудови кола, що проходить через дві відомі точки і що дотикається до відомого кола (будь-який з двох даних).Позначимо через N 1 і N 2 точки перетину прямої K 1 K 2 з 
і 
, відмінні від K 1 і K 2. Оскільки точки N 1 и K 1 переходять в K 2 и N 2 при гомотетії з центром Z, ми маємо пропорцію ZN 1/ ZK 1 = ZK 2/ ZN 2, ZK 1· ZK 2 = ZN 1· ZN 2. Тому (ZK 1· ZK 2)2 = ZK 1· ZK 2· ZN 1· ZN 2. З іншої сторони, d 1 = ZK 1· ZN 1 и d 2 = ZK 2· ZN 2– це ступені точки Z відносно кіл 
і ; отже (ZK 1· ZK 2)2 = d 1· d 2. При виведенні останньої рівності ми не користувалися тим 
, що K 1 і K 2 - це точки дотику. Воно залишиться справедливим, якщо замість K 1 взяти будь-яку точку L 1 на , а замість K 2 - точку L 2 перетину прямої ZL 1 з , відмінну від точки, відповідної L 1 при гомотетії кіл. Таким чином, ZA · ZX = ZK 1· ZK 2= ZL 1· ZL 2 для будь-якої такой пари точок L 1, L 2.Звідси випливає наступна побудова: проводимо довільну січну ZL 1 L 2, потім коло через точки L 1, L 2 і A і знаходимо X як точку перетину цього кола і з прямою ZA, відмінну від A. В результаті задача зводиться до випадку, коли дано дві точки (A і X) і коло. У цьому випадку, як ми бачили, є, взагалі кажучи, два рішення. Одне з них - це коло, що дотикається до обох даних зовнішнім чином, друге - коло, що дотикається до обох даних внутрішнім чином. Якщо виконати аналогічну побудову, взявши замість зовнішнього центру подібну внутрішньому, ми отримаємо ще два розв’язання (з різнойменним дотиком) (рис. Б. 5). Задача 2.1.6. Побудувати коло, що дотикається до трьох даних прямих. Розв’язання: Тут можливі кілька розв’язань (рис. Б. 6).Якщо прямі обмежують трикутник, то одне з них задається його вписаним колом, а ще три – не вписаних (що дотикаються до однієї зі сторін зовнішнього трикутника і продовжень двох інших сторін). Якщо паралельні рівно дві з трьох прямих, то розв’язання, очевидно, два, а якщо всі три, то жодного. Задача 2.1.7. Побудувати коло, що дотикаються до трьох даних кіл, які проходять через одну спільну точку Р (рис. Б. 7). Розв’язання: Якщо прийняти спільну точку трьох даних кіл за центр інверсії, то ці кола стануть трьома прямими. Таким чином, задача зводиться до побудови кола, що дотикаються до трьох побудованих прямих. Шукане коло – образ цього кола в даній інверсії.
2.2 Розв’язання задачі Аполлонія.
В першому підрозділі ми розглянули частинні випадки задачі Аполлонія, тепер можна перейти до розв’язання задачі Аполлонія в загальному випадку, але зупинитися на основних моментах цього розв’язання.
Розв’язання яке ми будемо досліджувати в нашому розділі, засноване на попередньому розв’язанні двох допоміжних задачах (представлена окремим випадком загальної задачі Аполлонія).
Перша допоміжна задача: побудувати коло яке дотикається до двох даних паралельних прямих і даного кола.
Задача зазвичай розв’язується методом геометричних місць. (Суть цього методу полягає в тому, що спочатку відкидають одну з умов задачі і будують геометричне місце точок, яке задовольняє другу умову; потім відкидають другу умову і будують геометричне місце точок, яке задовольняє першу умову. Перетин таких геометричних місць точок є шуканою точкою або іншим елементом шуканої фігури.)
Нехай а і в – дані прямі, γ (О, r) – дане коло (рис. В. 1). З довільної точки А на прямій а опускаємо перпендикуляр АВ на пряму в. Через середину С відрізка АВ проводимо пряму с паралельно а. Будуємо коло δ з центром в точці О радіуса 
(або радіуса 
). Відзначаємо точку перетину цього кола з прямою с; це і буде центр шуканого кола. Ця задача може мати до чотирьох розв’язань [12, с. 350-357].
Друга допоміжна задача: побудувати коло, що дотикається до трьох даних кіл, якщо два з них мають спільну точку.
Ця задача розв’язується методом інверсії. Нехай 
, 
– дані кола, причому і 
дотикаються в точці Т (рис. В. 2). Приймемо точку Т за центр інверсії, а за радіус інверсії – довільний відрізок (зручно вибрати його так, щоб базисне коло 
перетинала коло і ). При інверсії коло і переходять в пару паралельних прямих 
, а коло 
в деяке коло (або пряму) 
. Побудувати коло 
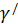, що дотикається до прямих і лінії , ми вміємо (дивитися першу допоміжну задачу). При інверсії це коло переходить в коло (або пряму) 
, котра буде дотикатися до даних кіл , 
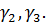
Розв’язання задачі Аполлонія в загальному випадку зводиться до цієї другої допоміжної задачі. Ми скористаємося для цього «методом розширення». Для визначення розглянемо той випадок, коли кожна з трьох даних кіл розташована поза двох інших (рис. В. 3). В наступних випадках розв’язання проводиться аналогічно.
Нехай 
– дані кола. Нехай, далі, пряма 
перетинає коло в точках 
а коло – в точках 
. З чотирьох відрізків 
, 
, 
виберемо найкоротший. Нехай цей відрізок буде . Позначимо через Т його середину. Збільшимо радіуси всіх даних кіл на відрізок 
, далі побудуємо коло 
(
), 
(
), 
(
). З них коло і 
дотикаються в точці Т, ми можемо тепер побудувати коло 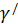, що дотикається до трьох кіл , (дивитися другу допоміжну задачу). Позначимо центр кола 
через О, а радіус – через 
. Якщо потім побудувати концентричне до нього коло 
+ 
то останнє коло буде дотикатися до трьох даних кіл [13, с. 203-214].
Число всіх можливих розв’язань задачі Аполлонія залежить від взаємного розташування даних кіл. Приведемо без доведення кілька прикладів.
1. Якщо коло розташоване в середині кола , а коло поза колом (рис. В. 4), то задача Аполлонія зовсім немає рішення. Це відноситься, зокрема і в випадку, коли три дані кола концентричні.
2. Якщо два кола і дотикаються, а трете коло перетинає їх в точці їх перетину то задача Аполлонія має два розв’язання 
(рис. В. 5).
3. Якщо кожна із даних кіл розташовані поза двох інших, причому дотична до кожних двох з даних кіл не має спільної точки з третім колом, то задача має вісім розв’язань (рис. В. 6).
4. Якщо всі три дані кола попарно дотикалися в одній точці, то можна провести нескінченно багато кіл, що дотикаються до кожної з даних (рис. В. 7).
Повне дослідження показує, що якщо задача Аполлонія має скінченне число розв’язань то їх не більше восьми:
Ці розв’язання залежать від того де буде присутня точка дотику шуканого кола з даними, тобто розв’язання задачі одне, а розміщення шуканого кола різне (рис. 2.2.1)
Рис. 2.2.1. Ілюстрація розв’язання задачі Аполлонія.
2.3 Розв’язання задач методом гіпербол які перетинаються и алгебраїчним методом.
В ході нашого дослідження ми з’ясували, що ті розв’язання задачі які ми розглянули вище, розв’язані методом інверсії, вони є загально відомі і на які звертають увагу при вивченні задач на побудову. Але ми з’ясували, що є розв’язання задач Аполлонія і іншими методами, ось два самих простих.
Метод гіпербол які перетинаються
Розв’язання Адріана ван Ромена (1596) заснований на перетині двох гіпербол [14]. Нехай дані кола позначаються як γ, ω, α. Адріан ван Ромен вирішив загальну проблему шляхом розв’язання більш простої задачі, знаходження кіл, дотична до двох даних кіл, таких як γ, ω. Він зазначив, що центр кола, дотичній до обох даних кіл повинні лежати на гіперболі, фокуси є центрами даних кіл. Щоб зрозуміти це, нехай радіус шуканого кола і два радіуси даних кіл позначаються як 
, 
, відповідно (рис. 2.3.1).
Рис. 2.3.1. Радіуси даних і шуканого кола.
Відстань 
між центрами шуканого кола і або 
або 
, в залежності від того, обрані ці кола, щоб бути зовнішнім або внутрішнім дотичним, відповідно. Аналогічно, відстань 
між центрами шуканого кола з або 
або 
, знову ж таки в залежності від обраного їх дотиків. Таким чином, різниця 
між цими відстанями завжди постійна, яка не залежить від . Це властивість, має фіксовану різницю між відстанями до фокусів, характеризує гіперболи, тому можливі центри кіл розв’язання лежать на гіперболі.Перетин двох гіпербол (якщо такі є) дає центр кола розв’язання, яке має обрані внутрішні і зовнішні дотичні до трьох даних кіл. Повний набір розв’язання задачі Аполлонія можна знайти, розглядаючи всі можливі комбінації внутрішнього і зовнішнього дотику кола розв’язання трьох даних кіл.
Алгебраїчне розв’язання
Проблема Аполлонія може бути оформлена у вигляді системи трьох рівнянь для центру і радіусу кола. [15, c. 116-126] Оскільки три заданих кола і будь-яке розв’язання кола повинні лежати в одній площині, їх позиції можуть бути визначені в інтервалах (х, у) координати їх центрів. Наприклад, в центрі розташування трьох даних кіл можна записати у вигляді (
, 
), (
, 
) і (
, 
), в той час як у колі розв’язання можна записати у вигляді (
, 
). Аналогічним чином, радіуси даних кіл розв’язання можна записати у вигляді 
, відповідно. Вимога про те, що розв’язання повинно точно дотикатися до кожного з трьох даних кіл можна це представити у вигляді трьох пов'язаних квадратичних рівнянь для , і 
:
Три числа 
на правій стороні, так звані знаки, можуть дорівнювати ± 1, і вказати, чи може шукане коло дотикатися до даного кола всередині (s = 1) або зовні (s = -1), Наприклад, на малюнках 1 і 4, червоне коло внутрішньо дотичній до розміру середньої заданої окружності справа і зовні дотичній до найменшого і найбільшого даних кіл на лівій; якщо дані кола впорядковані по радіусу, знаки для цього рішення "- + -". Оскільки три знака можуть бути обрані незалежно один від одного, існує вісім можливих наборів рівнянь (2 × 2 × 2 = 8), де кожен набір відповідає одному з восьми типів розв’язання кіл.
Загальна система трьох рівнянь може бути розв’язана за допомогою метода результанту. Коли перемножуються всі три рівняння мають 
+ 
на лівій стороні, і 
на правій стороні. Віднімаючи одне рівняння від іншого джерела усуває ці квадратичні члени; інші лінійні члени можуть бути перебудовані, щоб отримати формули для координат і
де M, N, P і Q є відомими функціями даних кіл. Заміна цих формул в одну з перших трьох рівнянь дає квадратне рівняння для ,які можуть бути розв’язані за допомогою квадратичної формули. Заміна числового значення , в лінійних формулах дає відповідні значення 
.
Знаки на правих частинах рівнянь можуть бути обрані в восьми можливих способів, і кожен вибір знаків дає до двох рішень, так як рівняння для є квадратним. Це дає підставу припустити (неправильно), що існує до шістнадцяти рішень завдання Аполлонія. Проте, через симетрії рівнянь, якщо (
) являє собою розв’язання, з ознаками, то і (- , 
), з протилежними знаками, що представляє собою одне і теж розв’язання. Таким чином, проблема Аполлонія має максимум вісім незалежних розв’язання (рис. 2.3.1).
Рис. 2.3.1. Розв’язання задачі Аполлонія.
ВИСНОВОК
В ході нашого дослідження нами було з’ясовано багатий репертуар геометричних і алгебраїчних методів які були розроблені для вирішення завдання Аполлонія. Ми дізналися з короткої біографії Аполлонія Пергського, що він прославився в першу чергу монографією «Конічні перерізи», але потім його головним завданням стало побудова кола яке дотикається до трьох заданих кіл. Оригінальне розв’язання Аполлонія його задачі було втрачено, але були реконструкції які запропонували інші математики такі як Вієт і інші, засновані на підказки в описі Папп. Перший новий метод вирішення був опублікований в 1596 році Адріаном ван Роменом, який визначив центри кіл розв’язання, як точки перетину двох гіпербол, метод Ромена було уточнено в 1687 році Ісаком Ньютон і Джоном Кейсі в 1881році.
Ми також розглянули етапи розв’язання геометричних задач на побудову, їх чотири: аналіз, побудова, доведення та дослідження. А також ми показали на прикладі як повинні за цими етапами розв’язуватися задачі на побудову.
В першому розділі третьому підрозділі ми розглянули та розв’язали основні задачі на побудову, такі як: побудова трикутника з даними сторонами a, b, c; побудова кута, що дорівнює даному; поділ відрізка навпіл; побудова бісектриси даного кута; побудова перпендикулярної прямої; побудова паралелограма за даними сторонами a і b і одного з кутів α; побудува квадрата за даною його діагоналлю АВ; побудова коло описаного навколо даного трикутника АВС; побудова вписаного коло в трикутник АВС; побудова коло описаного навкола даного прямокутника або квадрата АВСD; побудова вписаного коло в ромб (або квадрат) АВСD; побудова коло описаного навколо даного правильного багатокутника; побудова вписаного коло в даний правильний багатокутник; побудова вписаного квадрата в дане коло; побудова описаного квадрата навкола даного кола; побудова вписаного правильного п’ятикутника в дане коло; вписати в дане коло правильний шестикутник і трикутник; вписати правильний восьмикутник в дане коло; вписати правильний 10-кутник в дане коло; довкола даного кола описати правильний трикутник, п’ятикутник, шестикутник, восьмикутник, десятикутник.
В другому розділі ми перейшли до практичної частини, ми розв’язали сім допоміжних задач які допомагають розв’язати основну задачу Аполлонія. Потім ми перейшли до самого розв’язання задачі Аполлонія і з’ясували, що вона має аж вісім правильних розв’язань. В другому розділі ми дослідили ці розв’язання методом інверсії, який до речі найбільш зручний, простіший та зрозумілий. Але все одно це не єдиний метод розв’язання задачі, тому ми розглянули ще два методи: метод гіпербол які перетинаються та алгебраїчний метод. Успіх розв’язання цими методами був великий але незважаючи на це у вирішенні завдання Аполлонія, метод Ромена має недолік. Властивість зі знаменитої класичної евклідової геометрії є можливість вирішувати проблеми, використовуючи тільки компас і косинець. Неможливо, використовувати тільки ці інструменти, так як поділ кута на три рівні частини нереальні. Тим не менш, багато з таких «неможливо» проблеми можуть бути вирішені за допомогою пересічних кривих, таких як гіперболи, еліпси і параболи.
Отже задача Аполлонія має багато методів розв’язання, які заносяться в програму для пристроїв таких як GPS, навігаційні пристрої, а також пристрої стеження за тваринами.
ЛІТЕРАТУРА
1. Панов В. Ф. История науки и техники,/ В. Ф. Панов. 2006, с. 70—72.
2. Ван дер Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции // И. Н. Веселовского.— М.: Физматгиз, 1959. с. 338—339.
3. Белошістая, А.В. Задачі на побудову в шкільному курсі геометрії / А. В. Белошістая / / Математика в школі. - 2002. - № 9. - С. 47-50.
4. Панов В. Ф. Математика древняя и юная// В. Ф. Панов. — Изд. 2-е, исправленное. — М.: МГТУ им. Баумана, 2006. —с. 648 -650.
5. Рожанский И. Д. Античная наука // И. Д. Рожанский. — М.: Наука, 1980. — С. 140. — 198 с.
6. Атанасян Л. С. Геометрія: доп.глави до шк.учеб.8 кл.: Учеб.пособие для учнів шк.і класів з углубл.ізуч.математікі / Л. С. Атанасян, В.Ф. Бутузов, С.Д. Кадомцев и др. - М.: Просвещение, 1996.- с. 40-45.
7. Кисельов А. П. Геометрія: Планіметрія: 7-9 кл.: Підручник і задачник / А. П. Кисельов, Н.А. Рибкін. - М.: Дрофа, 1995.
8. Білозерової Л.І. Вивчення особистості школяра / під. ред. Л.І. Білозерової. - Кіров, Інформаційний центр, 1991. – с. 48-59
9. Коновалова, В.С. Рішення задач на побудову в курсі геометрії як засіб розвитку логічного мислення / В.С. Коновалова, З.В. Шилова / Пізнання процесівнавчання фізики: збірник статей. Вип.9. - К.: Вид-во ВятГГУ, 2008. - С. 59-69.
10. Хабелашвили А. В. Задача Аполлония Пергского // Историко-математические исследования, // А. В. Хабелашвили 1(36), часть 2, 1996, с. 66-81.
11. О.О. Барабанов Алгоритмы решения навигационной разностно-дальномерной задачи — от Аполлония до Коши // История науки и техники// Барабанов О. О., Барабанова Л.П. — М., 2008. — № 11. — С. 2-21.
12. Fried M. N. The use of analogy in Book VII of Apollonius’ Conica. Science in Context, 16, 2003, p. 349-365.
13. Hogendiuk J. P. Arabic traces of lost works of Apollonius. Archive for History of Exact Sciences, 35, 1986, p. 187-253.
14. van Roomen A (1596).Problema Apolloniacum quo datis tribus circulis, quaeritur quartus eos contingens, antea a…Francisco Vieta…omnibus mathematicis…ad construendum propositum, jam vero per Belgam…constructum(in Latin). Würzburg: Typis Georgii Fleischmanni. (Latin)
15. Coaklay GW (1860). "Analytical Solutions of the Ten Problems in the Tangencies of Circles; and also of the Fifteen Problems in the Tangencies of Spheres". The Mathematical Monthly 2: p. 116–126.
Не нашли, что искали? Воспользуйтесь поиском: