
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задания для контрольной работы №1
Самарский государственный университет путей сообщения
Кафедра высшей математики
 |
Контрольные задания
Для студентов заочной формы обучения
инженерно-технических специальностей
Часть 1

Cамара
УДК 519.7
Высшая математика: контрольные задания для студентов заочной формы обучения инженерно-технических специальностей. Часть 1 / Ю.В. Гуменникова, Л.В. Кайдалова, О.Е. Лаврусь. – Самара: СамГУПС, 2009. – 32 с.
Утверждены на заседании кафедры протокол № 9 от 11.06.09.
Печатаются по решению редакционно-издательского совета университета.
Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике для технических специальностей и охватывают разделы линейная алгебра, аналитическая геометрия, комплексные числа, введение в математический анализ, численные методы решения нелинейных уравнений.
В методических указаниях приведены индивидуальные задания, а также примеры решения задач.
Предназначены для студентов первого курса инженерно-технических специальностей заочной формы обучения.
Ил. 6. Табл. 5. Библиогр.: 9 назв.
Составители: Ю.В. Гуменникова, к. т. н., доцент,
Л.В. Кайдалова, к. ф.-м. н., доцент,
О.Е. Лаврусь, к. т. н., доцент
Рецензенты: к. ф.-м. н., доц. СамГУ Воскресенская Л.А.,
доцентСамГУПС Паняев В.А.
Ó Гуменникова Ю.В., Кайдалова Л.В., Лаврусь О.Е., 2009
Ó Самарский государственный университет путей сообщения, 2009
Задания для контрольной работы №1
Задание № 1
Решить систему линейных уравнений

методом Крамера и матричным методом. Сделать проверку.
Коэффициенты системы приведены в таблице 1.
Таблица 1
| № варианта | Коэффициенты системы линейных уравнений | |||||||||||
| а 11 | а 12 | а 13 | а 21 | а 22 | а 23 | а 31 | а 32 | а 33 | b 1 | b 2 | b 3 | |
| 1.1. | –1 | –5 | –3 | –1 | –17 | |||||||
| 1.2. | –1 | –6 | –2 | –1 | ||||||||
| 1.3. | –1 | –3 | –5 | –8 | ||||||||
| 1.4. | –1 | –1 | ||||||||||
| 1.5. | –3 | –1 | –1 | |||||||||
| 1.6. | –4 | –4 | ||||||||||
| 1.7. | –1 | –2 | –1 | |||||||||
| 1.8. | –1 | –3 | –5 | –7 | –4 | |||||||
| 1.9. | –9 | –5 | –7 | |||||||||
| 1.10. | ||||||||||||
| 1.11. | –2 | –4 | –2 | –5 | –7 | |||||||
| 1.12. | –3 | –3 | –2 | –7 | ||||||||
| 1.13. | –1 | |||||||||||
| 1.14. | –1 | –1 | –2 | –2 | –5 | –5 | ||||||
| 1.15. | –1 | –3 | ||||||||||
| 1.16. | –1 | –6 | –4 | –1 | –2 | –3 | ||||||
| 1.17. | –4 | –2 | –3 | –9 | ||||||||
| 1.18. | –5 | –1 | –3 | |||||||||
| 1.19. | –1 | |||||||||||
| 1.20. | –1 | –2 | –1 | |||||||||
| 1.21. | –1 | –10 | –5 | –7 | –6 | –2 | –8 | |||||
| 1.22. | –1 | –3 | –1 | –2 | –1 | –5 | ||||||
| 1.23. | –1 | –3 | –7 | –3 | –5 | –9 | ||||||
| 1.24. | –1 | –5 | –1 | –1 | –2 | –2 | ||||||
| 1.25. | –1 | –3 | –4 | |||||||||
| 1.26. | –2 | –3 | –1 | –9 | –22 | |||||||
| 1.27. | –4 | |||||||||||
| 1.28. | ||||||||||||
| 1.29. | –1 | –3 | ||||||||||
| 1.30. |
Задание № 2
Решить систему линейных уравнений АХ = В, заданной расширенной матрицей, методом последовательного исключения неизвестных. В случае неопределенности системы найти ее общее, базисное и любое частное решения. Сделать проверку.
2.1. 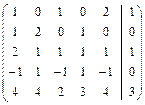 . 2.2.
. 2.2. 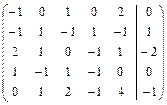 .
.
2.3. 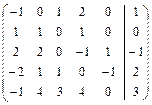 . 2.4.
. 2.4. 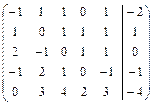 .
.
2.5.  . 2.6.
. 2.6.  .
.
2.7. 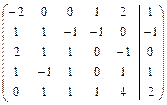 . 2.8.
. 2.8.  .
.
2.9. 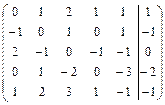 . 2.10.
. 2.10.  .
.
2.11.  . 2.12.
. 2.12.  .
.
2.13. 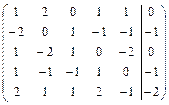 . 2.14.
. 2.14.  .
.
2.15. 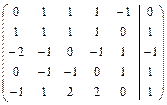 . 2.16.
. 2.16. 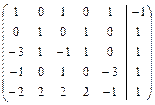 .
.
2.17. 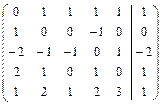 . 2.18.
. 2.18. 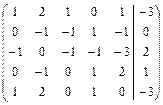 .
.
2.19. 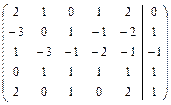 . 2.20.
. 2.20. 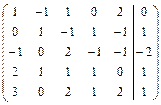 .
.
2.21. 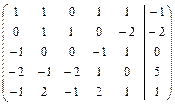 . 2.22.
. 2.22. 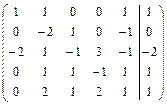 .
.
2.23. 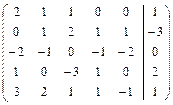 . 2.24.
. 2.24. 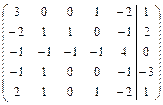 .
.
2.25.  . 2.26.
. 2.26. 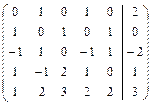 .
.
2.27. 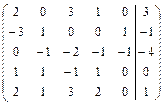 . 2.28.
. 2.28. 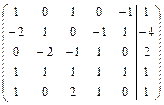 .
.
2.29.  . 2.30.
. 2.30. 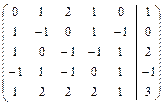 .
.
Задание № 3
По трем заданным точкам построить треугольник и средствами векторной алгебры найти: 1) длину стороны ВС; 2) уравнение линии ВС; 3) уравнение высоты, проведенной из точки А; 4) длину высоты, проведенной из точки А; 5) площадь треугольника АВС; 6) угол между сторонами ВА и ВС; 7) координаты точки N – середины стороны АС; 8) координаты точки М, делящей сторону АВ в отношении 2: 3, считая от точки А.
Координаты вершин треугольника даны в таблице 2.
Таблица 2
| № варианта | А | В | С | № варианта | А | В | С |
| 3.1. | (–2, 5) | (4, 5) | (1, 1) | 3.16. | (6, 9) | (5, –4) | (4, 6) |
| 3.2. | (–3, 1) | (4, –5) | (7, 2) | 3.17. | (2, 3) | (4, 0) | (5, 3) |
| 3.3. | (4, –1) | (4, 4) | (6, 4) | 3.18. | (8, 7) | (3, 0) | (5, 6) |
| 3.4. | (–5, 3) | (4, 6) | (8, 4) | 3.19. | (8, 1) | (3, 0) | (3, 5) |
| 3.5. | (0, –6) | (3, 5) | (–2, 4) | 3.20. | (1, 3) | (7, 10) | (3, 2) |
| 3.6. | (–2, –3) | (1, 6) | (5, 2) | 3.21. | (4, 0) | (6, 9) | (–2, 1) |
| 3.7. | (–6, 2) | (1, 8) | (4, 5) | 3.22. | (–2, 1) | (–2, 5) | (4, 0) |
| 3.8. | (1, 5) | (6, 5) | (5, 7) | 3.23. | (–2, 1) | (–3, 1) | (4, 10) |
| 3.9. | (5, –2) | (7, 2) | (5, 5) | 3.24. | (1, –2) | (4, –1) | (6, 9) |
| 3.10. | (5, –2) | (8, 4) | (6, 5) | 3.25. | (3, 1) | (3, 2) | (1, 2) |
| 3.11. | (9, 6) | (2, 3) | (4, 0) | 3.26. | (–1, –1) | (0, 4) | (1, –1) |
| 3.12. | (7, 5) | (4, 0) | (1, 2) | 3.27. | (1, –1) | (–2, –3) | (4, 5) |
| 3.13. | (4, 7) | (–3, 2) | (3, –2) | 3.28. | (–2, 0) | (–1, 2) | (3, 4) |
| 3.14. | (7, 3) | (0, 6) | (6, 8) | 3.29. | (3, 2) | (1, 2,) | (6, 6) |
| 3.15. | (4, 9) | (2, 4) | (5, 7) | 3.30. | (0, 4) | (–2, –4) | (6, 6) |
Задание № 4
По четырем заданным точкам построить пирамиду и средствами векторной алгебры найти: 1) длину ребра А 1 А 2; 2) угол между ребрами А 1 А 2 и А 1 А 4; 3) площадь грани А 1 А 2 А 3; 4) объем пирамиды А 1 А 2 А 3 А 4; 5) составить уравнение прямой А 1 А 2; 6) уравнение плоскости А 1 А 2 А 3.
Координаты вершин пирамиды даны в таблице 3.
Таблица 3
| № варианта | А 1 | А 2 | А 3 | А 4 |
| 4.1. | (1, 1, 1) | (–1, 2, 4) | (2, 0, 6) | (–2, 5, –1) |
| 4.2. | (0, 5, 0) | (2, 3, –4) | (0, 0, –6) | (–3, 1, –1) |
| 4.3. | (0, 0, 6) | (4, 0, –4) | (1, 3, –1) | (4, –1, –3) |
| 4.4. | (2, –5, 3) | (3, 2, –5) | (5, 3, 2) | (–5, 3, 2) |
| 4.5. | (6, 0, 4) | (0, 6, 4) | (4, 6, 0) | (0, –6, 4) |
| 4.6. | (3, 2, 4) | (2, 4, 3) | (4, 3, –2) | (–2, –4,–3) |
| 4.7. | (6, 3, 5) | (5, –4, 3) | (3, 5, 6) | (–6, –1, 2) |
| 4.8. | (5, –2, –1) | (4, 0, 0) | (2, 5, 1) | (1, 2, 5) |
| 4.9. | (4, 2, 5) | (3, 0, 4) | (0, 0, 3) | (5, –2, –4) |
| 4.10. | (4, 2, –5) | (3, 0, 4) | (0, 2, 3) | (5, –2, –4) |
| 4.11. | (4, 4, 10) | (7, 10, 2) | (2, 8, 4) | (9, 6, 9) |
| 4.12. | (4, 6, 5) | (6, 9, 4) | (2, 10, 10) | (7, 5, 9) |
| 4.13. | (3, 5, 4) | (8, 7, 4) | (5, 10, 4) | (4, 7, 8) |
| 4.14. | (10, 6, 6) | (–2, 8, 4) | (6, 8, 9) | (7, 10, 3) |
| 4.15. | (1, 8, 2) | (5, 2, 6) | (5, 7, 4) | (4, 10, 9) |
| 4.16. | (6, 6, 5) | (4, 9, 5) | (4, 6, 11) | (6, 9, 3) |
| 4.17. | (7, 2, 2) | (5, 7, 7) | (5, 3, 1) | (2, 3, 7) |
| 4.18. | (8, 6, 4) | (10, 5, 5) | (5, 6, 8) | (8, 10, 7) |
| 4.19. | (7, 7, 3) | (6, 5, 8) | (3, 5, 8) | (8, 4, 1) |
| 4.20. | (–2, 1, 2) | (4, 0, 0) | (3, 2, 7) | (1, 3, 2) |
| 4.21. | (3, 2, 7) | (1, 3, 2) | (–2, 1, 2) | (4, 0, 0) |
| 4.22. | (1, 3, 2) | (3, 2, 7) | (4, 0, 0) | (–2, 1, 2) |
| 4.23. | (3, 1, –2) | (1, –2, 1) | (2, 2, 5) | (–2, 1, 0) |
| 4.24. | (–2, 1, 0) | (2, 2, 5) | (3, 1, 2) | (1, –2, 1) |
| 4.25. | (2, 2, 5) | (–2, 1, 0) | (1, –2, 1) | (3, 1, 2) |
| 4.26. | (1, –1, 6) | (4, 5, –2) | (–1, 3, 0) | (1, –1, 5) |
| 4.27. | (6, 1, 5) | (–1, 3, 0) | (4, 5, –2) | (1, –1, 6) |
| 4.28. | (1, –2, 1) | (3, 1, –2) | (2, 2, 5) | (–2, 1, 0) |
| 4.29. | (4, 0, 0) | (–2, 1, 2) | (1, 3, 2) | (3, 2, 7) |
| 4.30. | (–5, 6, –1) | (6, –5, 2) | (6, 5, 1) | (0, 0, 2) |
Задание № 5
Даны уравнения линии r = r (j) в полярной системе координат. Требуется: 1) построить линию по точкам на промежутке от j = 0 до j = 2p с шагом, равным p / 8; 2) найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) назвать линию, найти координаты центра и полуоси.
5.1. 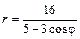 . .
| 5.2.  . .
| 5.3. 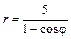 . .
|
5.4. 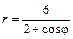 . .
| 5.5.  . .
| 5.6. 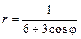 . .
|
5.7. 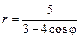 . .
| 5.8. 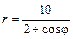 . .
| 5.9. 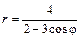 . .
|
5.10. 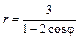 . .
| 5.11. 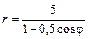 . .
| 5.12.  . .
|
5.13. 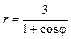 . .
| 5.14. 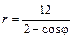 . .
| 5.15.  . .
|
5.16.  . .
| 5.17.  . .
| 5.18. 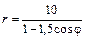 . .
|
5.19.  . .
| 5.20.  . .
| 5.21. 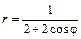 . .
|
5.22. 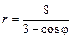 . .
| 5.23.  . .
| 5.24. 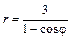 . .
|
5.25. 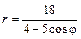 . .
| 5.26. 
| 5.27.  . .
|
5.28. 
| 5.29. 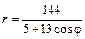 . .
| 5.30.  . .
|
Решение типового варианта КР № 1
2Задание 1. Решить СЛУ методом Крамера и матричным методом. Сделать проверку найденного решения.

Решение. Метод Крамера. Составим и вычислим определитель системы D и вспомогательные определители (полученные из D заменой столбца коэффициентов при соответствующей неизвестной столбцом свободных членов) разложением по элементам первой строки
D= 
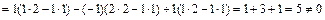 ;
;
 ;
;  ;
; 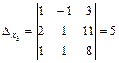 ;
;
тогда
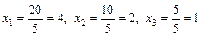 .
.
Сделаем проверку
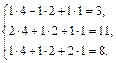 Þ Х = (4, 2, 1).
Þ Х = (4, 2, 1).
Матричный метод. Обозначим
 ,
, 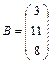 .
.
Найдем
1) определитель 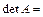

 .
.
Следовательно, матрица невырожденная и существует 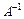 .
.
2) транспонированную матрицу 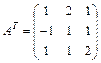 .
.
3) союзную матрицу 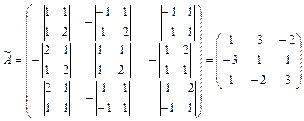 .
.
4) обратную матрицу  .
.
Находим решение системы X = А –1 В:


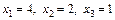 .
.
Ответ: Х = (4, 2, 1). v
2Задание 2. Решить систему линейных уравнений АХ = В, заданной расширенной матрицей, методом последовательного исключения неизвестных. В случае неопределенности системы найти ее общее, базисное и любое частное решения. Сделать проверку.
 .
.
Решение. Возьмем переменную х 3 в первом уравнении за базисную и исключим ее из второго и третьего уравнений системы. Для этого умножим первое уравнение на (+2) и сложим со вторым. Для исключения х 3 из третьего уравнения умножим первое уравнения на (+1) и сложим с третьим:
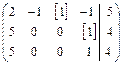 .
.
Возьмем в другой строке новую базисную переменную х 4 и исключим ее из первого и третьего уравнений. Вычеркнем строку, содержащую одни нули.
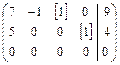 Þ
Þ 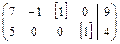 .
.
Итак, базисными переменными будут х 3, х 4.
Разрешим полученные уравнения относительно базисных переменных. Остальные (небазисные) переменные называются свободными (х 1 и х 2).
Выражение базисных переменных через свободные называется общим решением СЛУ.
В нашем случае общее решение имеет вид
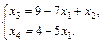
Если в общем решении приравнять свободные переменные нулю, то получим базисное решение
 .
.
Если в общем решении свободным переменным давать произвольные значения, то получим множество частных решений.
Пусть х 1 = 1, х 2 = –1 Þ  ;
;
х 1 = 0, х 2 = 2 Þ  .
.
Сделаем проверку, подставив, например, базисное решение в СЛУ:
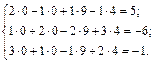
Ответ: Общее решение 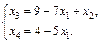 Базисное решение
Базисное решение  , частное решение
, частное решение  . v
. v
2 Задание 3. По трем заданным точкам А (3, 1), В (–13, –11), С (–6, 13) построить треугольник и средствами векторной алгебры найти: 1) длину стороны ВС; 2) уравнение линии ВС; 3) уравнение высоты, проведенной из точки А; 4) длину высоты, проведенной из точки А; 5) площадь треугольника АВС; 6) угол между сторонами ВА и ВС; 7) координаты точки N – середины стороны АС; 8) координаты точки М, делящей сторону АВ в отношении 2: 3, считая от точки А.
Решение. Чертеж треугольника приведен на рисунке 1.
1. Вычислим координаты вектора 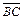 , где В (х 1, у 1, z 1), С (х 2, у 2, z 2), по формуле
, где В (х 1, у 1, z 1), С (х 2, у 2, z 2), по формуле 
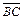 = (–6 – (–13); 13 – (–11)) = (7, 24).
= (–6 – (–13); 13 – (–11)) = (7, 24).

Вычислим длину вектора по формуле 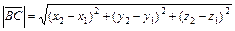
 =
= 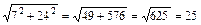 .
.
2. Запишем уравнение прямой ВС в виде 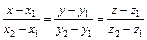 :
:
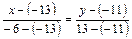 Þ
Þ 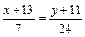 Þ
Þ  Þ
Þ 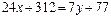 .
.
Уравнение прямой ВС: 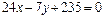 .
.
3. Уравнение высоты АD может быть получено различными способами.
1 способ. Заметим, что вектор 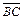 является нормальным вектором для прямой АD и точка А (3, 1) принадлежит прямой АD, следовательно,
является нормальным вектором для прямой АD и точка А (3, 1) принадлежит прямой АD, следовательно,
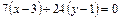 Þ
Þ 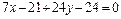 .
.
Итак, АD: 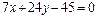 .
.
2 способ. Запишем уравнение высоты, проведенной из точки А в форме уравнения прямой с угловым коэффициентом k, при этом воспользуемся свойствами угловых коэффициентов взаимно перпендикулярных прямых.
Определим угловой коэффициент прямой ВС. Для этого разрешим уравнение прямой относительно у, имеем
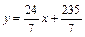 Þ
Þ 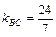 Þ
Þ 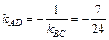 .
.
Подставим полученные данные в уравнение прямой, проходящей через точку М (х 0, у 0), перпендикулярно данной прямой y = k 1 x + b, которое имеет вид 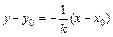 , и получим
, и получим  .
.
Запишем полученное уравнение в форме общего уравнения плоскости:
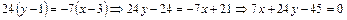 .
.
Заметим, что результаты в первом и втором слyчаях совпадают.
Итак, прямая АD задается уравнением 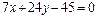 .
.
4. Длину высоты АD также можно определить различными способами.
1 способ. Поскольку координаты точки А известны, найдем координаты точки D. Заметим, что точка D лежит на пересечении прямых ВС и АD, следовательно, ее координаты удовлетворяют уравнениям обеих прямых. Составляем систему из уравнений, задающих прямые ВС и АD:
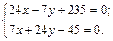
Решим систему по формулам Крамера:
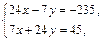 Þ
Þ  ,
,
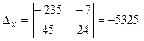 ,
, 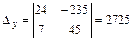 ,
,
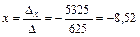 ;
;  Þ D (–8,52; 4,36).
Þ D (–8,52; 4,36).
Теперь воспользуемся формулой для вычисления длины отрезка
 .
.
2 способ. Длину отрезка АD можно рассматривать как расстояние от точки А (3, 1) до прямой ВС (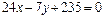 ), поэтому воспользуемся формулой
), поэтому воспользуемся формулой 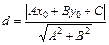 , где (x 0, y 0) – координаты точки А, Ах + Ву + С = 0 – уравнение прямой:
, где (x 0, y 0) – координаты точки А, Ах + Ву + С = 0 – уравнение прямой:
 .
.
5. Найти площадь треугольника АВС. В предыдущих пунктах были определены величина основания 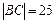 и длина высоты
и длина высоты 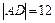 . Поэтому целесообразно применить формулу
. Поэтому целесообразно применить формулу  . Имеем
. Имеем 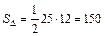 (кв. ед.).
(кв. ед.).
6. Для вычисления величины угла между сторонами ВА и ВС (угол a) воспользуемся формулой 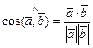 :
:
 ,
,  ,
,
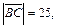
 .
.
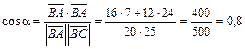 .
.
a= аrcсos 0,8 = 36°50¢ (если воспользоваться калькулятором или компьютером, то результат может быть записан в виде 36,87°).
7. Для нахождения координат середины отрезка АС воспользуемся формулами  ;
; 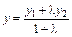 ;
; 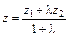 , где l = 1.Имеем
, где l = 1.Имеем
 Þ
Þ 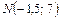 .
.
8. Координаты точки М, найдем по формулам  ;
; 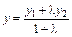 ;
; 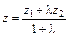 , где l = 2 / 3:
, где l = 2 / 3:
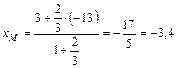 ;
; 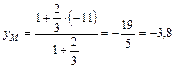 .
.
Окончательно 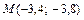 .
.
Ответ:  = 25; уравнение прямой ВС:
= 25; уравнение прямой ВС: 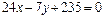 ; уравнение прямой АD:
; уравнение прямой АD: 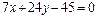 ;
; 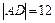 ;
; 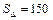 (кв. ед.); a= 36°50¢;
(кв. ед.); a= 36°50¢; 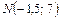 ;
; 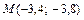 . v
. v
2 Задание 4. По четырем заданным точкам А 1(4, 2, 5), А 2(0, 7, 2), А 3(0, 2, 7), А 4(1, 5, 0) построить пирамиду и средствами векторной алгебры найти: 1) длину ребра А 1 А 2; 2) угол между ребрами А 1 А 2 и А 1 А 4; 3) площадь грани А 1 А 2 А 3; 4) объем пирамиды А 1 А 2 А 3 А 4; 5) уравнение прямой А 1 А 2; 6) уравнение плоскости А 1 А 2 А 3.
 Чертеж пирамиды приведен на рисунке 2.
Чертеж пирамиды приведен на рисунке 2.
1. Найдем координаты и длину вектора 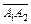 :
:
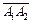 =
=  ,
,

 .
.
2. Для определения угла j, вычислим координаты и модули векторов, направленных по сторонам этого угла:
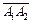
 ,
,  ;
;
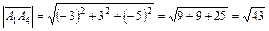 .
.
Угол определим по формуле
 .
.
По таблицам находим 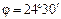 .
.
3. Для вычисления площади грани А 1 А 2 А 3 воспользуемся свойствами векторного произведения двух векторов, на которых построен треугольник А 1 А 2 А 3, и формулой  :
:
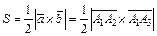 ,
, 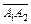 = (–4, 5,–3),
= (–4, 5,–3), 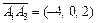 ,
,
 =
=  ,
,
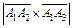
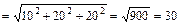 Þ
Þ 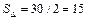 (кв. ед.).
(кв. ед.).
4. Для вычисления объема воспользуемся формулой смешанного произведения:
 ,
, 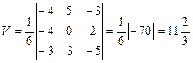 (куб. ед.).
(куб. ед.).
5. Для определения уравнения прямой А 1 А 2 воспользуемся уравнением 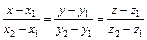 . Имеем
. Имеем
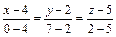 ,
,
окончательно получаем уравнение прямой А 1 А 2
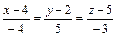 .
.
6. Уравнение плоскости А 1 А 2 А 3 запишем в форме уравнения плоскости, проходящей через три точки по формуле  :
:

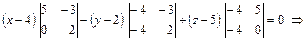
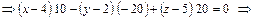
 .
.
Разделим обе части уравнения на 10, окончательно уравнение плоскости А 1 А 2 А 3 примет вид x + 2 y + 2 z – 18 = 0.
Ответ:  ;
; 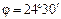 ;
; 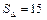 (кв. ед.);
(кв. ед.);
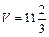 (куб. ед.); уравнение прямой А 1 А 2:
(куб. ед.); уравнение прямой А 1 А 2: 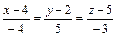 ;
;
уравнение плоскости А 1 А 2 А 3: x + 2 y + 2 z – 18 = 0. v
2 Задание 5 Даны уравнения линии  в полярной системе координат. Требуется: 1) построить линию по точкам на промежутке от j = 0 до j = 2p с шагом, равным p / 8; 2) найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) назвать линию, найти координаты центра и длины полуосей.
в полярной системе координат. Требуется: 1) построить линию по точкам на промежутке от j = 0 до j = 2p с шагом, равным p / 8; 2) найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) назвать линию, найти координаты центра и длины полуосей.
Решение. Составим таблицу 4 для вычисления значений r.
Таблица 4
| j | p / 8 | p / 4 | 3p / 8 | p / 2 | 5p / 8 | 3p / 4 | 7p / 8 | p | … | |
| cos j | 0,92 | 0,71 | 0,38 | –0,38 | –0,71 | –0,92 | –1 | … | ||
| r | 1,04 | 1,15 | 1,38 | 1,80 | 2,59 | 4,14 | 6,90 | … |
 |
Построим линию, учитывая, что
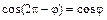 (рисунок 3).
(рисунок 3).
Для перехода в декартовую систему координат воспользуемся формулами
 ,
, 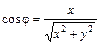 .
.
Получим уравнение
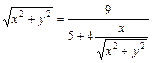 ,
,
которое после преобразований примет вид
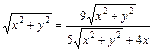 Þ
Þ 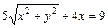 Þ
Þ
 Þ
Þ 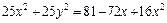 Þ
Þ  ,
,
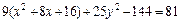 Þ
Þ 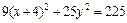 Þ
Þ 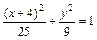 .
.
Получили уравнение эллипса с центром в точке О ¢(–4; 0) и полуосями а = 5, b = 3 (рисунок 4).
Ответ: уравнение эллипса с центром в точке
О (–4; 0) и полуосями а = 5, b = 3. v
Не нашли, что искали? Воспользуйтесь поиском: