Разложение функций в степенной ряд

Вопрос представления функции многочленом Тейлора мы рассматривали еще в первом семестре. Естественно поставить вопрос разложения функции в степенной ряд. Учитывая предыдущую информацию, можно определить следующий алгоритм разложения функции f(x) в степенной ряд в окрестности заданной точки х ₀:

1. Найти производные заданной функции до п -го порядка включительно (т.е. записать формулу для f ^(п)(x)) и вычислить их значения в точке х ₀.

2. Записать формально ряд Тейлора для f (x).

3. Найти область сходимости этого ряда.

4. Выяснить, для каких х из области сходимости ряда выполняется условие 0

Пример 1. Разложим функцию е^х в ряд в окрестности точки х = 0 (ряд Тейлора с центром в точке х = 0 называется рядом Маклорена). Будем пользоваться сформулированным алгоритмом.

1. Очевидно, f ^(п)(x) = е^х, тогда f ^(п)(0) = 1

2. ряд Тейлора имеет вид

3. Радиус сходимости этого ряда найдем, используя формулу . Так как , то , значит, ряд сходится на всей числовой прямой.

4. Изучим поведение остатка ряда. Запишем остаток ряда в форме Лагранжа:

à , где 0 < |x| < | x |. Заметим, что здесь – некоторое (конечное) число, а – (п +1)-й член рассмотренного ряда Тейлора, а так как ряд сходится " х, то его п -й член (а значит и п +1-й) стремится к 0 при возрастании п. Тогда

" х.

Значит, е^х = , х Î R.

Пример 2. Разложим в ряд Маклорена функцию f (x) = sin x. Имеем:

f (x) = sin x, f (0) = 0

f¢ (x) = cos x = sin , f ¢(0) = 1

f¢¢ (x) = –sin x = sin (x + p), f ¢¢(0) = 0

f¢¢¢ (x) = –cos x = sin , f ¢¢¢(0) = –1

f ^IV(x) = sin x = sin (x + 2p), f ^IV(0) = 0,

.....................

f ⁽ⁿ⁾(x) = sin , f ^{(2 k)}(0) = 0, f ^{(2 k –1)}(0) = (–1) ^{k +1}.

Тогда ряд Тейлора имеет вид

Найдем область сходимости этого ряда:

< 1" х

Значит, область сходимости – вся числовая прямая.

Остаток ряда в форме Лагранжа имеет вид

Тогда | R_n (x)| = и

, значит " х.

Таким образом, " х Î R.

Учитывая свойства степенных рядов, находим, продифференцировав полученное разложение:

То есть имеем разложение cos x = , " х Î R.

Ранее мы получили разложения

, | x |< 1, и , х Î(-1; 1].

Если в первом из этих равенств положить х = t ², получим

, или, в привычных символах, , х Î(-1; 1).

Проинтегрировав последнее равенство, получим

, т.е.

, х Î(-1; 1).

Заметим, что в граничных точках полученный ряд сходится условно:

при х = –1 имеем , а при х = 1 получаем ; оба эти ряда сходятся по признаку Лейбница (проверьте!). Ряд из модулей членов этих рядов один и тот же и он расходится, что можно без труда доказать, пользуясь интегральным признаком. Тот факт, что данные ряды сходятся соответственно к arctg(–1) = и arctg1 = мы сможем доказать позже, изучив тригонометрические ряды. Итак, , х Î[-1; 1].

Пользуясь вышеописанным алгоритмом можно получить следующее разложение

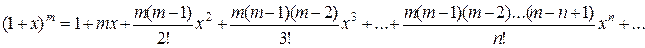, х Î(-1,1).

Таким образом, мы имеем перечень известных разложений:

I. е^х = , х Î R

II. " х Î R

III. cos x = , " х Î R.

IV. , | x |< 1,

V. , | x |< 1.

VI. , х Î(-1; 1].

VII. , х Î[-1; 1].

VIII. , | x | < 1

Как следует из рассмотренных примеров, разложение в ряд заданной функции можно осуществить двумя способами: по определению (т.е. пользуясь описанным алгоритмом) и пользуясь известными разложениями, делая разного рода подстановки, дифференцируя или интегрируя ряд почленно.

Рассмотрим другие примеры разложений.

Пример 3. Разложить заданные функции по степеням х

1) ,

-3 х Î(-1; 1] à ,

итак "

2)

Найдем интервал сходимости полученного ряда: х Î(-1; 1) и Î(-1; 1), откуда .

Пример 4. Разложить функцию f (x) по степеням х – х ₀.

1) f (x) = , х ₀ = 4.

,

.

Итак, , х Î(-2;10)

2) f (x) = cos² x, х ₀ = .

,

.

Не нашли, что искали? Воспользуйтесь поиском: