Это можно переписать в виде свертки

E ₁(x, h) = E (x, y)* h ₁(x, y, x, h),

где

h ₁(x, y; x, h) =

– импульсный отклик первого слоя свободного пространства, – координаты в плоскости линзы. Соотношение (11.7) описывает зависимость между входом и выходом аналога линейной системы и выражает тот факт, что распределение комплексного светового поля непосредственно перед линзой обусловлено распределением комплексного светового поля в плоскости предмета.

После прохождения линзы поле в плоскости непосредственно за линзой будет

E ₁¢(x, h) = E ₁(x, h) t (x, h) P (x, h).

Оптический сигнал E ₁¢(x, h) является входным сигналом второй системы – второго свободного пространства глубиной а′. Поле в плоскости изображения найдется как свертка функции E ₁¢(x, h) с импульсным откликом

h ₂(x, h, x¢, y¢) =

второго свободного пространства:

= E ₁ ¢(x, h)* h ₂(x, h, x¢, y¢).

Таким образом, поле в плоскости изображения

= {[ E (x, y)* h ₁(x, y, x, h)] t (x, h)

P (x, h)}* h ₂(x, h, x¢, y¢).

Это выражение можно записать в интегральной форме:

=

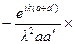
(11.8)

Мы видим, что распределение поля в плоскости изображения можно представить как результат двойной дифракции световой волны от плоскости объекта до плоскости линзы и от плоскости линзы до плоскости изображения (подробнее об этом в п. 11.7). Произведение множителя перед интегралом на двойной интеграл по x, h от экспоненциального множителя обозначим через h (x¢ – – x, y¢ – y). Тогда поле можно представить в виде интеграла свертки:

= , (11.9)

где

. (11.10)

Функцию называют импульсной характеристикой (или функцией пропускания) элементарной оптической системы. Она представляет собой поле точечного источника в точке (x, y), рассматриваемое в точке плоскости изображения X′Y ′. Раскрыв скобки в экспоненциальном множителе, после некоторых преобразований для импульсной функции будем иметь

h (x, y, x¢, y¢)

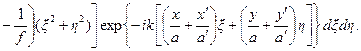
(11.11)

По указанным в предыдущем параграфе соображениям фазовые множители перед интегралом в не зависящие от переменных интегрирования x, y, можно положить равными единице. Если считать, что 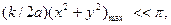т.е. если , первый квадратичный фазовый множитель тоже можно положить равным единице. А поскольку a и a′ удовлетворяют формуле линзы, то и квадратичный фазовый множитель в подынтегральном выражении будет равен единице. С учетом этого для импульсной функции идеальной элементарной оптической системы будем иметь

=

(11.12)

Полученное выражение показывает, что с точностью до постоянного множителя перед интегралом импульсная функция элементарной оптической системы представляет собой фурье-образ функции зрачка на пространственных частотах 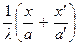и . Можно сказать, что импульсный отклик элементарной оптической системы есть дифрагировавшее на оправе линзы поле точечного источника (в приближении Фраунгофера).

Введем величину называемую коэффициентом линейного увеличения линзы. Подставив в выражение (11.12) значение a = a ′ / b и учтя, что k = 2 p / l, выражение для импульсной функции представим в виде

=

Произведем замену переменных x / la′ = x ₁, h / la′ = y ₁. Тогда получим

=

. (11.13)

Положим теперь, что зрачковая функция P (la′x ₁, la′y ₁) = 1. Это допущение предполагает, что линза перехватывает все лучи, идущие со стороны предмета. Тогда интеграл (11.13) будет представлять собой d -функцию и, следовательно,

≈ – b d (x¢ + b x, y¢ + b y)

или, учитывая, что d (mx, ny) = d (x, y),

= d .

Подставляя это в интеграл суперпозиции (11.9), для распределения поля в плоскости изображения получим

E′ (x¢, y¢) =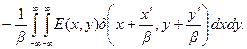

Учитывая фильтрующее свойство d -функции, окончательно находим

E′ (x¢, y¢) = . (11.14)

Мы видим, что каждой точке (x, y) предмета соответствует определенная точка (x¢, y¢) изображения, как и должно быть по геометрической теории оптических изображений. Распределение поля в плоскости изображения получается заменой в распределении поля в плоскости предмета координат x и y на координаты – x¢ / b и – y¢ / b и умножением поля на коэффициент 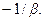Световое поле в плоскости изображения изменяется обратно пропорционально коэффициенту линейного увеличения линзы. При этом изменяется масштаб осей в b раз, а их направление – на обратное. Таким образом, изображение, получающееся в пренебрежении конечными размерами и аберрациями линзы, представляет собой точную копию предмета, увеличенную в b раз и перевернутую в плоскости изображения, т.е. точно такое, какое получается в геометрической оптике.

В приближении геометрической оптики, которое имеет место при l ® 0, функция зрачка P (la′x ₁, la′y ₁) принимается равной единице при всех значениях переменных x ₁ и y ₁. Действительно, если радиус оправы линзы равен R, то функция зрачка P (la′x ₁, la′y ₁) = 1 для всех la′x ₁ и la′y ₁, лежащих внутри круга

Отсюда получаем Следовательно, при l ® 0 имеем x ₁ ® ¥, y ₁ ® ¥. Очевидно, что переход к пределу l ® 0 равносилен переходу к линзе неограниченных размеров (R ® ¥). Линза, неограниченных размеров и не имеющая аберраций, называется идеальной. Идеальная линза дает идеальное изображение – геометрически подобное предмету.

Соотношение (11.14) показывает, что рассматриваемая оптическая система является линейной по отношению к комплексной амплитуде. Но так и должно быть при когерентном освещении. В идеальной оптической системе (в смысле геометрической оптики) формирования изображения, как мы видели, импульсная функция является d -функцией. Соответствующая передаточная функция

H (u, v) =

= .

Так как в итоге регистрируется интенсивность изображения, то интерес представляет величина Эта величина равна единице при всех u и v. Следовательно, идеальная оптическая система формирования изображения имеет передаточную характеристику с неограниченной полосой пространственных частот.

Следует отметить также, что при выполнении формулы линзы квадратичный фазовый множитель в подынтегральном выражении (11.11), т.е. тот, который приводит к искажению изображения при распространении света в свободном пространстве, исчезает. Тем самым линза, как уже отмечалось, компенсирует действие свободного пространства между предметом и линзой и между линзой и изображением.

Полученные выше выражения и выражения, которые будут получены ниже в этой главе, можно считать справедливыми для любой оптической системы, формирующей изображение. Все конструктивные усложнения реальных систем служат для того, чтобы приблизить их свойства к свойствам идеализированной тонкой линзы. Дифракционные эффекты, возникающие в сложной системе можно интерпретировать как эффекты дифракции на входном зрачке системы.

Рассмотрим случай, когда a′ = f, т.е. плоскость X¢Y¢ является задней фокальной плоскостью линзы. Оптическую систему будем считать идеальной, т.е. что P = 1. Импульсная функция элементарной оптической системы (11.11) в этом случае принимает вид

(11.15)

Интеграл в этом выражении можно вычислить, используя формулу (9.21). Полагая

a = , b ₁ = , b ₂ = ,

получим

=

= ×

.

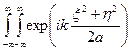
Тогда получим

=

.

Фазовый множитель

Не нашли, что искали? Воспользуйтесь поиском: