Коэффициент осцилляции

Основные формулы по общей теории статистики

При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала по формуле

k = 1 + 3,32lg N = 1,44ln N + 1,

где k – число групп; N – численность совокупности.

Суммируя число всех единиц с одинаковыми значениями признака, получаем N, то есть

.

Индекс динамики характеризует изменение какого-либо явления во времени. Данный индекс определяется по формуле:

,

где цифры означают: 1 – отчетный или анализируемый период, 0 – прошлый или базисный период.

Критериальным значением индекса динамики служит единица (или 100%), то есть если >1, то имеет место рост (увеличение) явления во времени; если =1 – стабильность; если <1 – наблюдается спад (уменьшение) явления.

Еще одно название индекса динамики – индекс изменения, вычитая из которого единицу (100%), получают темп изменения (динамики) с критериальным значением 0, который определяется по формуле:

.

Если T >0, то имеет место рост явления; Т =0 – стабильность, Т <0 – спад.

Индекс планового задания – это отношение планового значения признака к базисному. Он определяется по формуле:

,

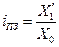где X’₁ – планируемое значение; X₀ – базисное значение признака.

Для определения процента выполнения плана необходимо рассчитать индекс выполнения плана по формуле:

.

Индекс структуры (доля) – это отношение какой-либо части объекта (совокупности) ко всему объекту. Он определяется по формуле:

Индекс координации – это отношение какой-либо части объекта к другой его части, принятой за основу (базу сравнения). Он определяется по формуле:

.

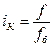Индекс сравнения – это сравнение (соотношение) разных объектов по одинаковым признакам. Он определяется по формуле:

,

где А, Б – сравниваемые объекты.

Индекс интенсивности – это соотношение разных признаков одного объекта между собой. Он определяется по формуле:

.

где X – один признак объекта; Y – другой признак этого же объекта

Средняя арифметическая обобщает индивидуальные значения Хi суммированием, а равномерное распределение – делением суммы Хi на число единиц, участвующих в расчете:

n

S x_i

i=1

x _арифм = ---------------- или

n

Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

Сумма отклонений значений признака от арифметической средней равна нулю:

n

S (x_i - x _арифм) = 0

i=1

Если значения признака Х_i изменить на число А, то арифметическая средняя изменится на это же число:

n

S (x_i ± A)

i=1

----------------------- = x _арифм ± A

n

Если значения признака Х_i увеличить в А раз, то арифметическая средняя увеличится в А раз

n

S (x_i * A)

i=1

----------------------- = x _арифм * A

n

Если значения признака Хi уменьшить в А раз, то арифметическая средняя также уменьшится в А раз:

n

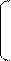S x_i

i=1 A

----------------------- = x _{арифм / A}

n

Средняя арифметическая взвешенная:

(2)

fi – вес (частота) i – го признака.

Средняя гармоническая используется в тех случаях, когда расчет выполняется по значениям признака, который связан с изучаемым признаком обратной зависимостью, т.е. при условии, что V определяется по значениям признака

t = ------

V

Например, показатель выработки продукции на работника:

Продукция Q

V = ---------------------- = ------

Работники T

Показатель трудоемкости единицы продукции:

Работники Т

t = ----------------- = -----

Продукция Q

Показатели выработки и трудоемкости находятся в обратной зависимости

1 1

V = ------, а t = --------

t V

Поэтому при расчете средней выработки по значениям трудоемкости следует применять гармоническую среднюю

n

V = ------

n

S 1

i=1 V

Когда статистическая информация не содержит частот f по отдельным вариантам X_i совокупности, а представлена как их произведение Xf, тогда применяется формула средней гармонической взвешенной, для получения которой обозначим Xf=w, откуда f=w/X, и, подставив эти обозначения в формулу 2, получим формулу:

.

Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны действительные веса f, а известно w=Xf. В тех случаях, когда вес каждого варианта w =1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:

. Или

f – варианты, xi – отдельные варианты; n – число вариантов осредняемого признака.

Средняя квадратическая применяется в случаях, когда при обобщении значений признака Mi необходимо избежать нулевого результата, так как

n

S М_i = 0

i=1

Для этого значения признака возводят в квадрат: M ² i , из суммы квадратов

n

S М_i ²

i=1

n

S М_i ²

i=1

рассчитывают среднюю М² = ----------------

n, а из полученной средней извлекают квадратный корень:

n

S М_i ²

i=1

М = Ö М² = ----------

Ö n

Средняя квадратическая простая

Средняя квадратическая взвешенная рассчитывается по другой формуле:

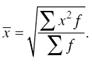
Свойство мажорантности средних можно представить в виде неравенств:

V < K < x < M

Средняя геометрическая

n

К₁ * К₂ * К₃ * … * К _n = П Кi простая

i=1

а из результата извлекается корень n-й степени:

^{n n} n

К = Ö К₁ * К₂ * К₃ * … * К _n = П Кi взвешенная

Ö i=1

Средняя геометрическая простая рассчитывается по формуле

или

Формула средней геометрической взвешенной имеет следующий вид:

или

Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

где – средняя величина; – индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.

Степенные средние.

Мода (Мо) – величина признака, которая чаще всего встречается в данной совокупности.

где х0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; fm_ 1 – частота предшествующего интервала; fm+ 1 – частота следующего интервала.

Медианой (Ме) называется вариант, расположенный в центре ранжированного ряда.

Ме

где X0 – нижняя граница интервала; h – величина интервала; fm – частота интервала; f – число членов ряда; ò_m-1 – сумма накопленных членов ряда, предшествующих данному.

Абсолютные показатели вариации:

– Размах вариации - R

– Среднее линейное отклонение – d

– Дисперсия – σ²

– Среднее квадратическое отклонение – σ

– Квартильное отклонение (d_k)

Измеряются в тех же единицах, что и сам признак: т; м; с; руб. (кроме σ²)

Относительные показатели вариации:

– Коэффициент осцилляции (относительный размах вариации)

– Линейный коэффициент вариации (относительное линейное отклонение)

– Коэффициент вариации

Измеряются в процентах или относительных величинах.

Размах вариации (R) - это разность между максимальным и минимальным значениями вариант признака.

С помощью этого показателя определяют допустимые размеры колебания, сравнивают их с установленными

X_max – наибольшее значение признака

X_min – наименьшее значение признака

R = Х_max – X _min

Среднее линейное отклонение простое (для несгруппированных данных (первичного ряда)):

S çx_i - X ç

d _пр = ------------------

n

Среднее линейное отклонение (d) – среднее отклонение вариант признака x_i от средней величины Х без учета их знака.

Если отдельные варианты имеют частоту повторений (¦_i), то каждое отклонение повторяется ¦_i раз.

Среднее линейное отклонение взвешенное (для вариационного ряда):

S (x_i - X) ¦_i

d _взв = ------------------

S ¦_i

Дисперсия, или средний квадрат отклонений (s²), характеризует среднее значение квадрата отклонений вариант признака x_i от средней величины X.

Дисперсия простая (для несгруппированных данных)

S (x_i - X) ²

s² пр = ----------------------

N

Если отдельные варианты имеют частоту повторений ¦_i, то каждый квадрат отклонений повторяется ¦_i раз. В таком случае рассчитывается дисперсия взвешенная.

Дисперсия взвешенная (для вариационного ряда)

S (x_i - X) ² ¦_i

s² взв = ------------------

S ¦_i

Формула для расчета дисперсии может быть преобразована:

n n n n n

S (x – x)² S [(x ²i – 2 x_ix + (x)²] S x ²i – 2 x Sx_i + n(x)²] S x_i ²

i=1 i=1 i=1 i=1 i=1

s² = ^{--------------------------} = ^{--------------------------------------} = ^{------------------------------------------------ = -----------------} - (x)²

n n n n

Следовательно,

s² = x² – (x)²

Среднее квадратическое отклонение ( s) – квадратный корень из дисперсии:

s = Ös²

Коэффициент вариации (К_вар) характеризует степень однородности совокупности и рассчитывается по формуле

s

К_вар = ---------- 100 %.

х

Совокупность считается однородной, если К_вар < 33%.

Квартильное отклонение (d_k) применяется вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений:

Q₃ – Q₁

d_k = -------------------

где Q₃ и Q₁ - соответственно третья и первая квартили распределения.

Формулы расчета относительных показателей вариации приведены ниже:

Коэффициент осцилляции

R

K_R = -------- * 100%

x

Не нашли, что искали? Воспользуйтесь поиском: