ПРАКТИЧЕСКИЙ ПРИМЕР 10: ПРОВЕДЕНИЕ КРИВОЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

Очень часто возникает необходимость выразить в виде функциональной зависимости связь между величинами, которые заданы в виде набора точек с координатами (x, y).

Предположим, например, что в результате некоторого эксперимента получены точки, отложенные на графике рис. 8.13. Если необходимо использовать эти данные для вычислений на ЭЦВМ, то сразу появляются следующие проблемы:

1. В значениях у наверняка имеются погрешности эксперимента. Было бы желательно каким-либо образом «сгладить» те отклонения, которые обусловлены ошибками эксперимента.

2. Может оказаться желательным знать значения у, соответствующие промежуточным значениям х.

3. Может оказаться, что необходимо экстраполировать функциональную зависимость, т.е. найти значение у,

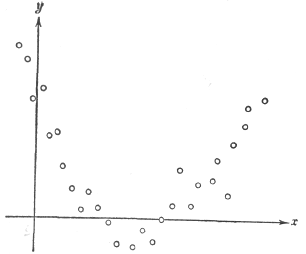
Рис. 8.13. Пример экспериментальных результатов, для которых ищется приближенная функциональная зависимость (практический

пример 10).

соответствующее значению x, лежащему вне области эксперимента (иногда это является главной целью эксперимента и вычислений). В особенности это относится к экономической информации.

Все эти соображения приводят нас к выводу, что желательно было бы установить некоторую функциональную зависимость между x и y в виде по возможности простой формулы. Вопрос состоит в том, как найти кривую, которая приближенно соответствует исходной информации c до статочной точностью. Таким образом, нужно выработать критерий, согласно которому та или иная кривая является достаточно «хорошим» приближением к исходной информации.

Рассуждение станет проще, если мы, введем новое понятие. Назовем отклонением экспериментальной точки разность между экспериментальной ординатой y и той, которая вычислена из функциональной зависимости. Вопрос о том, является ли кривая достаточно «хорошим» приближением к экспериментальным данным, можно поставить в следующем виде: какое условие необходимо наложить на отклонение точек от кривой, чтобы эта кривая представляла экспериментальные данные с достаточной точностью?

Казалось бы, что наиболее простое и логичное условие состоит в том, чтобы сумма отклонений точек от кривой была наименьшей. Если обозначить через y' значение y, вычисленное из функциональной зависимости, то это условие можно записать так: требуется, чтобы

было минимальным, причем в этом выражении N означает количество точек исходной информации. Но привлекательность этого простого критерия сразу становится сомнительной, стоит только рассмотреть простую задачу о проведении линии через две точки, как это показано на рис. 8.14. Мы видим, что пунктирная линия удовлетворяет нашему критерию, но прямую линию, изображенную на этом рисунке, никак нельзя признать удовлетворительным приближением к экспериментальным данным. Можно попытаться обойти это затруднение, используя в критерии сумму абсолютных значений отклонений, т. е. требуя, чтобы

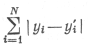
стало минимальным. Но в этом случае для нахождения минимума нельзя воспользоваться производной, так как абсолютное значение не имеет производной в точке минимума. Можно было бы наложить условие, согласно которому максимальное отклонение должно стать наименьшим (приближение Чебышева), но для определения функциональной зависимости на основе этого критерия приходится использовать длинную и сложную итерационную процедуру. Поэтому в данном случае мы воспользуемся критерием наименьших квадратов, т.е. будем искать такую функциональную зависимость, при которой обращается в минимум. Это выражение, как мы увидим ниже, можно продифференцировать для нахождения минимума. Такой критерий во многих практических случаях приводит к линейным уравнениям, которые легко решить, по крайней мере в принципе.

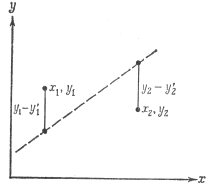
Рис.8.14. Пример, показывающий, что сумма отклонений не может служить критерием для подбора функциональной зависимости (практический пример 10).

Наконец, можно статистически обосновать, что критерий наименьших квадратов дает достаточно хорошее приближение функциональной зависимости к экспериментальным данным, даже если отвлечься от вопроса о практике вычислений.

Рассмотрим теперь вопрос о том, как при использовании критерия наименьших квадратов получается система уравнений для определения функциональной зависимости y от x. Сначала мы произведем вычисления для очень простой зависимости, а именно квадратичной, а затем рассмотрим, что получается, если выбирать другие типы функций[4].

Напишем

Наша задача состоит в том, чтобы определить значения c₁, c₂ и с₃, при которых сумма[5] становится минимальной.

Известно, что в минимуме функции ее производная равна нулю. Рассматривая S как функцию c₁, мы приравниваем нулю частную производную от S по c₁. При этом получается

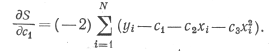
Приравнивая нулю и преобразовывая, получаем

Аналогичным образом, дифференцируя S по с₂ и по с₃ и приравнивая нулю соответствующие выражения, получаем еще два уравнения для определения неизвестных с₁, с₂ и с₃. Эти уравнения называются нормальными уравнениями для выбора наилучшего приближения к экспериментальным точкам в виде квадратичной параболы (подчеркиваем еще раз, что вид функциональной зависимости задан заранее)

Теперь для определения коэффициентов с₁, с₂ и с₃ достаточно вычислить суммы и решить систему из трех уравнений.

Тот же метод можно использовать при выводе нормальных уравнений для многочлена любой степени, к которым желательно приблизить экспериментальную зависимость. (В дальнейшем, однако, мы увидим, что использование многочленов очень больших степеней невозможно из-за ошибок округления.)

Нормальные уравнения для нахождения коэффициентов многочлена степени М можно написать в следующем виде:

Для многочлена степени М получается система из М+1 уравнений относительно М+1 коэффициентов. Количество сумм, которое необходимо вычислить, равно 3М+1.

Напомним, что индексы в ФОРТРАНе должны быть положительными. В приведенной ниже программе коэффициенты c_i образуют одномерный массив и поэтому нумеруются во всех формулах с 1.

Перед тем, как переходить к рассмотрению, программы по вычислению требуемых сумм и решению нормальных уравнений, отметим, что метод наименьших квадратов можно применить и к другим функциональным зависимостям, а не только к многочленам. Предположим, например, что мы ищем зависимость в виде показательной функции

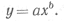
Непосредственное использование метода наименьших квадратов приведет к нелинейным нормальным уравнениям, но это затруднение можно обойти, используя вместо экспериментальных значений их логарифмы

Теперь мы стараемся сделать минимальной сумму квадратов разностей между логарифмами экспериментальных значений y_i и логарифмами ординат функции y=ax^b. При этом получаем

Дифференцируя по a и по b, придем к системе нормальных уравнений

Неизвестными в этой системе являются log а и b. После их определения a находится по величине логарифма.

В принципе метод наименьших квадратов можно применить для любой функциональной зависимости, хотя нормальные уравнения часто получаются нелинейными. Не которые типы функциональных зависимостей рассмотрены в упражнениях.

Вернемся теперь к обобщенной программе для нахождения полиномиальных приближений к экспериментальным Данным методом наименьших квадратов. С помощью этой программы можно будет работать с многочленами любой степени до 10-й включительно, причем необходимую степень можно будет прочитать с перфокарты. В программе будет предусмотрен ввод экспериментальных данных, вычисление необходимых сумм, решение нормальных уравнений и печать результатов.

[1] Система уравнений называется неприводимой, если нельзя вычислить какие-либо неизвестные, решая меньше чем n уравнений.

[2] В действительности для любой невырожденной системы уравнений существуют итерационные методы решения, но обычно они неудобны для практических вычислений. См., например, книгу Milne W. Е., Numerical solution of differential equations, Wiley, 1953.

[3] В некоторых случаях в треугольной системе после исключения все же остаются нулевые коэффициенты (см. упражнение 10).

[4] Предполагается, естественно, что вид функциональной зависимости задан заранее. С помощью метода наименьших квадратов невозможно установить, например, что экспонента была бы хорошим приближением, если не попытаться фактически ее испробовать. Короче говоря, при использовании этого метода можно находить наилучшее приближение заданного типа; вообще никакой метод не способен определить тип функциональной зависимости, который лучше всего подошел бы к данному набору экспериментальных точек.

[5] Для читателей, непривычных к обращению с суммами, мы приводим несколько простых тождеств, в которых через a обозначена некоторая ненулевая константа, а через x_i и y_i — некоторые переменные:

В дальнейшем мы будем подразумевать, что суммы вычисляются по всему массиву, т. е, символ будет означать

Не нашли, что искали? Воспользуйтесь поиском: