
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение. Поверхностный интеграл называется потоком векторного поля через поверхность D.
Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P(x, y, z) по кривой АВ в направлении от А к В.
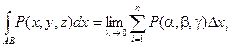
Криволинейный интеграл второго рода, т.е. интеграл по координатам отличается от криволинейного интеграла первого рода, т.е. по длине дуги тем, что значение функции при составлении интегральной суммы умножается не на длину частичной дуги, а на ее проекцию на соответствующюю ось. (В рассмотренном выше случае – на ось ОХ).
Вообще говоря, криволинейные интегралы могут считаться также и по переменным у и z.
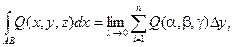
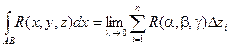
 Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.
Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.
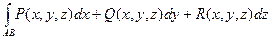
Свойства криволинейного интеграла второго рода.
1) Криволинейный интеграл при перемене направления кривой меняет знак.
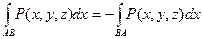
2) 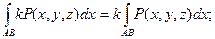
3) 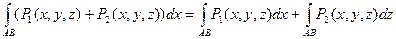
4) 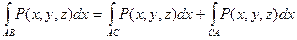
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.
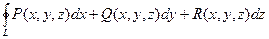
Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.
6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то
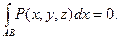
Аналогичные соотношения справедливы при интегрировании по переменным у и z.
Теорема. Если кривая АВ – кусочно- гладкая, а функции P(x, y, z), Q(x, y, z) и
R(x, y, z) – непрерывны на кривой АВ, то криволинейные интегралы
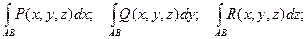
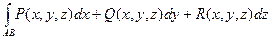
существуют.
Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:

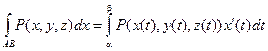
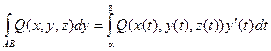
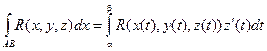
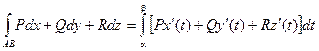
В случае, если АВ – плоская кривая, заданная уравнением y = f(x), то

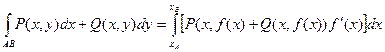
Пример. Вычислить криволинейный интеграл 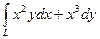 . L – контур, ограниченный параболами
. L – контур, ограниченный параболами 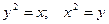 . Направление обхода контура положительное.
. Направление обхода контура положительное.



Представим замкнутый контур L как сумму двух дуг L1 = x2 и 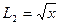
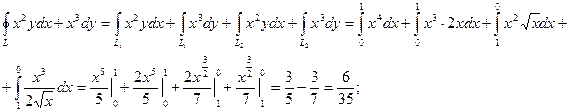
Формула Остроградского – Грина.
(Остроградский Михаил Васильевич (1861-1862) – русский математик,
академик Петерб. А.Н.)
(Джордж Грин (1793 – 1841) – английский математик)
Иногда эту формулу называют формулой Грина, однако, Дж. Грин предложил в 1828 году только частный случай формулы.
Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.
Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
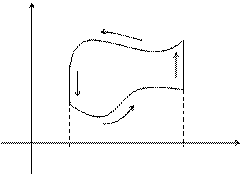 y
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
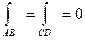

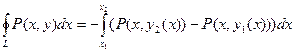
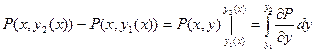
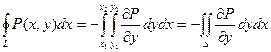
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:

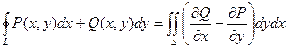
Эта формула называется формулой Остроградского – Грина.
Формула Остроградского – Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область D все время оставалась по левую сторону линии обхода.
Пример. Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.

Формула Остроградского – Грина позволяет значительно упростить вычисление криволинейного интеграла.
Криволинейный интеграл не зависит от формы пути, если он вдоль всех путей, соединяющих начальную и конечную точку, имеет одну и ту же величину.
Условием независимости криволинейного интеграла от формы пути равносильно равенству нулю этого интеграла по любому замкнутому контуру, содержащему начальную и конечную точки.
Это условие будет выполняться, если подынтегральное выражение является полным дифференциалом некоторой функции, т.е. выполняется условие тотальности.
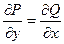
Поверхностные интегралы первого рода.
z
DSi
y
D
x
Поверхностный интеграл является таким же обобщением двойного интеграла, каким криволинейный интеграл является по отношению к определенному интегралу.
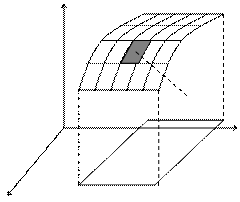
Рассмотрим поверхность в пространстве, которая произвольно разбита на n частей.
Рассмотрим произведение значения некоторой функции F в произвольной точке с координатами (a, b, g) на площадь частичного участка DSi, содержащего эту точку.
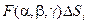
Определение. Если при стремлении к нулю шага разбиения l поверхности существует конечный предел интегральных сумм, то этот предел называется поверхностным интегралом первого родаили интегралом по площади поверхности.

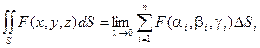
Свойства поверхностного интеграла первого рода.
Поверхностные интегралы первого рода обладают следующими свойствами:
1)  S – площадь поверхности.
S – площадь поверхности.
2) 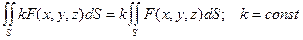
3) 
4) Если поверхность разделена на части S1 и S2, то
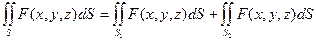
5) Если 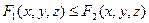 , то
, то
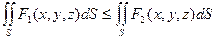
6) 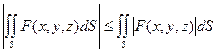
7) Теорема о среднем.
Если функция F(x, y, z) непрерывна в любой точке поверхности S, то существует точка (a, b, g) такая, что
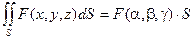
S – площадь поверхности.
Проведя рассуждения, аналогичные тем, которые использовались при нахождении криволинейного интеграла, получим формулу для вычисления поверхностного интеграла первого рода через двойной интеграл по по площади проекции поверхности на плоскость XOY.


Поверхностные интегралы второго рода.
Если на поверхности S есть хотя бы одна точка и хотя бы один не пересекающий границу поверхности контур, при обходе по которому направление нормали в точке меняется на противоположное, то такая поверхность называется односторонней.
Если при этих условиях направление нормали не меняется, то поверхность называется двухсторонней.
Будем считать положительным направлением обхода контура L, принадлежащего поверхности, такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остается слева.
Двухсторонняя поверхность с установленным положительным направлением обхода называется ориентированной поверхностью.
Рассмотрим в пространстве XYZ ограниченную двухстороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан либо уравнением вида z = f(x, y), либо является цилиндрической поверхностью с образующими, параллельными оси OZ.
Определение. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы, составленные как суммы произведений значений некоторой функции на площадь частичной поверхности, имеют конечный предел, то этот предел называется поверхностным интегралом второго рода.

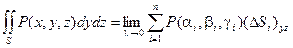
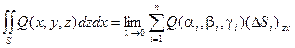

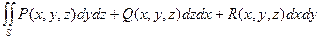
- поверхностный интеграл второго рода.
Свойства поверхностного интеграла второго рода аналогичны уже рассмотренным нами свойствам поверхностного интеграла первого рода.
Т.е. любой поверхностный интеграл второго рода меняет знак при перемене стороны поверхности, постоянный множитель можно выносить за знак интеграла, поверхностный интеграл от суммы двух и более функций равен сумме поверхностных интегралов от этих функций, если поверхность разбита на конечное число частичных поверхностей, интеграл по всей поверхности равен сумме интегралов по частичным поверхностям.
Если S- цилиндрическая поверхность с образующими, параллельными оси OZ, то 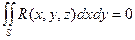 . В случае, если образующие поверхности параллельны осям OX и OY, то равны нулю соответствующие составляющие поверхностного интеграла второго рода.
. В случае, если образующие поверхности параллельны осям OX и OY, то равны нулю соответствующие составляющие поверхностного интеграла второго рода.
Вычисление поверхностного интеграла второго рода сводится к вычислению соответствующих двойных интегралов. Рассмотрим это на примере.
Пример. Вычислить интеграл  по верхней стороне полусферы
по верхней стороне полусферы
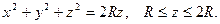
Преобразуем уравнение поверхности к виду: 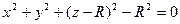
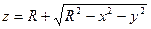
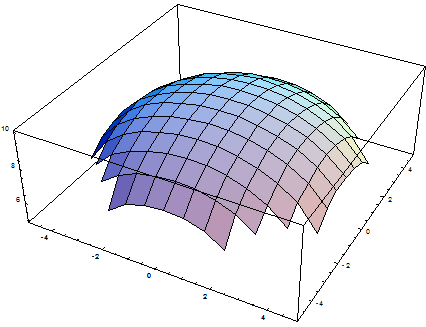
Заданная поверхность проецируется на плоскость XOY в круг, уравнение которого:
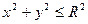
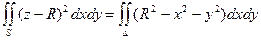
Для вычисления двойного интеграла перейдем к полярным координатам:
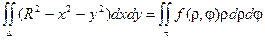 ,
, 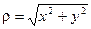
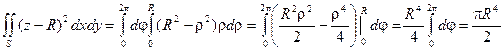
Связь поверхностных интегралов первого и второго рода.
Поверхностные интегралы первого и второго рода связаны друг с другом соотношением:

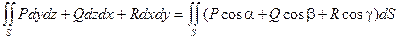
В этой формуле cosa, cosb, cosg - направляющие косинусы нормали к поверхности S в выбранную сторону поверхности.
Формула Гаусса – Остроградского.
Формула Гаусса – Остроградского является аналогом формулы Грина – Остроградского. Эта формула связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью.
Для вывода формулы Гаусса – Остроградского надо воспользоваться рассуждениями, подобными тем, которые использовались при нахождении формулы Грина – Остроградского.
Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум доугим координатным осям.
После этого полученные результаты обобщаются, приводя к формуле Гаусса – Остроградского:

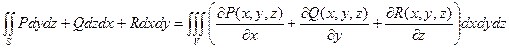
Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.
На практике формулу Гаусса – Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.
Тиеют место формулы:

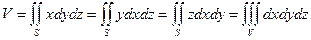
Пример. Найти формулу вычисления объема шара.
В поперечных сечениях шара (сечения параллельны плоскости XOY) получаются окружности.
Уравнение шара имеет вид: 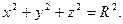
Найти объем шара можно по формуле:
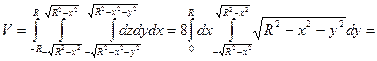
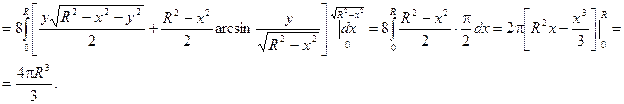
Для решения этой же задачи можно воспользоваться преобразованием интеграла к сферическим координатам. Это значительно упростит интегрирование.
Элементы теории поля.
Определение. Если каждой точке пространства М ставится в соответствие некоторая скалярная величина U, то таким образом задается скалярное поле U(M). Если каждой пространства М ставится в соотвтствие вектор 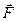 , то задается векторное поле
, то задается векторное поле  (М).
(М).
Пусть в пространстве М задана поверхность D. Будем считать, что в каждой точке Р определяется положительное направление нормали единичным вектором 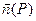 .
.
В пространстве М зададим векторное поле, постовив в соответствие каждой точке точке пространства вектор, определенный координатами:
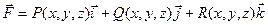
Если разбить каким – либо образом поверхность на частичные участки Di и составить сумму 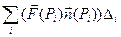 , где
, где 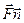 - скалярное произведение, то предел этой суммы при стремлении к нулю площадей частичных участков разбиения (если этот предел существует) будет поверхностным интегралом.
- скалярное произведение, то предел этой суммы при стремлении к нулю площадей частичных участков разбиения (если этот предел существует) будет поверхностным интегралом.
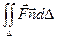
Определение. Поверхностный интеграл называется потоком векторного поля через поверхность D.
Если поверхность разбита на конечное число частичных поверхностей, то поток векторного поля через всю поверхность будет равен сумме потоков через частичные поверхности.
Если преобразовать скалярное произведение в координатную форму, то получаем соотношение:
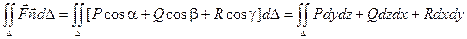
Если на области D существует функция f(x, y, z), имеющая непрерывные частные производные, для которых выполняются свойства:
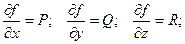
то такую функцию называют потенциальной функцией или потенциалом вектора 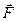 .
.
Тогда вектор 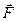 является градиентом функции f.
является градиентом функции f.
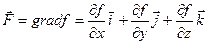
Потенциал может быть найден по формуле:


В этой формуле x0, y0, z0 – координаты некоторой начальной точки. В качестве такой точки удобно брать начало координат.
Теорема. Для того, чтобы поле вектора 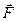 , заданного в некоторой области, имело потенциал, необходимо и достаточно, чтобы выполнялось одно из двух условий:
, заданного в некоторой области, имело потенциал, необходимо и достаточно, чтобы выполнялось одно из двух условий:
1) Интеграл от вектора 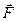 по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.
по любому кусочно – гладкому контуру, принадлежащему области, равен нулю.
2) Интеграл по любому кусочно – гладкому пути, соединяющему две любые точки поля не зависит, от пути интегрирования.
Формула Стокса.
(Джордж Габриель Стокс (1819 – 1903) – английский математик)
Формула Стокса связывает криволинейные интегралы второго рода с поверхностными интегралами второго рода.
Пусть в пространстве задана некоторая поверхность S. L – непрерывный кусочно – гладкий контур поверхности S.
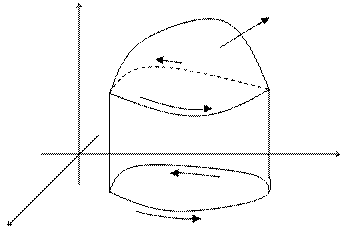
z S
L
y
D
l
x
Предположим, что функции P,Q и R непрерывны на поверхности S вместе со своими частными производными первого порядка. Применим формулу, выражающую криволинейный интеграл через определенный.
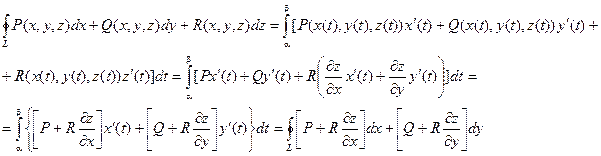
Введем обозначения: 
Применив формулу Грина – Остроградского, можно заменить криволинейный интеграл равным ему двойным интегралом. После преобразований устанавливается следуюшее соответствие между криволинейным и поверхностным интегралом:


эта формула и называется формула Стокса.
Определение. Вектор 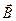 , компоненты которого равны соответственно равны
, компоненты которого равны соответственно равны
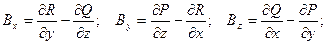
называется вихрем или ротором вектора 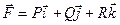 и обозначается:
и обозначается:

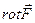
Определение. Символический вектор  называется оператором Гамильтона. (Уильям Роуан Гамильтон (1805 – 1865) – ирландский математик) Символ Ñ - “набла”.
называется оператором Гамильтона. (Уильям Роуан Гамильтон (1805 – 1865) – ирландский математик) Символ Ñ - “набла”.
С учетом этого обозначения можно представить себе понятие ротора вектора 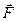 как векторного произведения оператора Гамильтона на вектор
как векторного произведения оператора Гамильтона на вектор 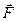 .
.


Определение. Криволинейный интеграл, представляющий собой работу векторного поля вдоль некоторой кривой L называется линейным интегралом от вектора 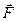 по ориентированной кривой L.
по ориентированной кривой L.

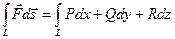
Если кривая L представляет собой замкнутый контур, то линейный интеграл по такому контуру называется циркуляцией вектроного поля 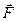 вдоль контура L.
вдоль контура L.

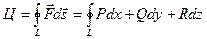
В векторной форме теорему Стокса можно сформулировать так:
Циркуляция вектора вдоль контура некоторой поверхности равна потоку вихря (ротора) через эту поверхность.

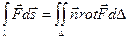
Отметим, что рассмотренная выше формула Грина – Остроградского является частным случаем формулы Стокса.
Также при условии равенства нулю всех компонент ротора вектора, получаем, что криволинейный интеграл по любой пространственной кривой равен нулю, т.е. криволинейный интеграл не зависит от пути интегрирования.
Определение. Выражение 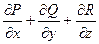 называется дивергенцией вектора (дивергенцией векторной функции)
называется дивергенцией вектора (дивергенцией векторной функции) 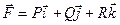 и обозначается
и обозначается

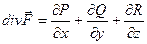
Таким образом, формулу Гаусса – Остроградского может быть записана в виде:

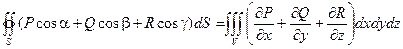
или
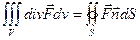
т.е. интеграл от дивергенции векторного поля 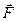 по объему равен потоку вектора через поверхность, ограниченную этим объемом.
по объему равен потоку вектора через поверхность, ограниченную этим объемом.
Определение. Векторное поле 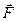 называется соленоидальным (трубчатым), если div
называется соленоидальным (трубчатым), если div 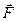 =0.
=0.
C помощью описанного выше оператора Гамильтона можно представить определенные нами понятия следующим образом:

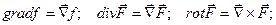
Как было сказано выше, выражение
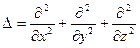
называется оператором Лапласа.
Справедливы следующие соотношения:

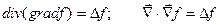
Справедливость этих равенств легко проверить непосредственной подстановкой.
Теперь рассмотрим примеры применения рассмотренных выше понятий.
Пример. Найти 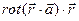 , если
, если 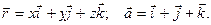
Найдем скалярное произведение: 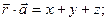
Найдем скалярное произведение:
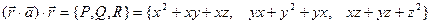

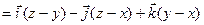
Пример. Найти поток векторного поля 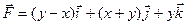 через сторону треугольника S, вырезанного из плоскости
через сторону треугольника S, вырезанного из плоскости 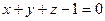 координатными плоскостями.
координатными плоскостями.
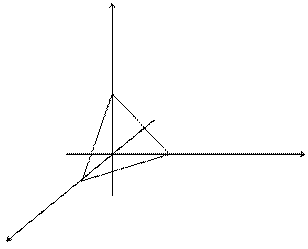 z
z
x = 1 – z z = 1 - y
x
y = 1 - x
y
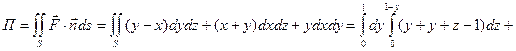
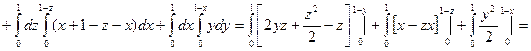
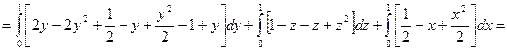
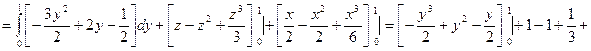
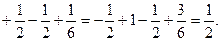
Пример. Найти div(grad u), если 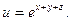
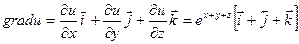
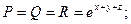
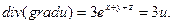
Пример. Определить является ли векторное поле потенциальным
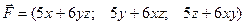
и найти его потенциал.
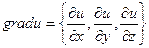

Если поле потенциально, то должны выполняться следующие условия:
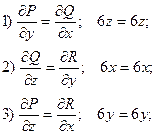
Эти условия эквивалентны условию равенства нулю ротора векторного поля. справедливость этого утверждения видна из формулы ротора.
Таким образом, поле потенциальное. Потенциал находится по формуле:
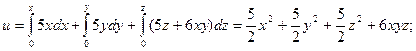
| <== предыдущая лекция | | | следующая лекция ==> |
| Техника эндоскопического гемостаза | | | ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ |
Не нашли, что искали? Воспользуйтесь поиском: