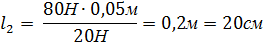Простые механизмы. Рычаг. Равновесие сил на рычаге

С развитием цивилизации человечество нуждалось в приспособлениях, которые бы увеличивали человеческую силу. Это было необходимо при строительстве, подъеме различных тяжестей, а также в сельскохозяйственной деятельности.

Например, для поднятия тяжелого камня, который человек не в состоянии поднять без приспособлений, используют длинную палку – рычаг.

Так в Древнем Египте с помощью рычагов были подняты тяжелые каменные глыбы во время строительства пирамид.

Для поднятия груза на высоту используют так же наклонную плоскость и блок или систему блоков.

Эти приспособления получили название простые механизмы. Механизмы – это приспособления для преобразования силы. К простым механизмам относятся – рычаг и его разновидности, ворот и блок, а так же наклонная плоскость и ее разновидности, клин и винт.

Если рассмотреть устройство любого сложного механизма, то легко увидеть в нем сочетание этих шести видов простых механизмов. С их помощью выполняются различные операции: ковка, разка, штамповка и многие другие.

Одним из часто встречаемых простых механизмов является рычаг. Поговорим о нем более подробно.

Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры. Точкой О обозначена неподвижная опора. В зависимости от того как расположены силы, различают рычаг первого и второго рода. Рычаг первого рода – силы направлены по разные стороны от опоры О. Рычаг второго рода – силы направлены по одну сторону от опоры О.

И в первом и во втором случае мы видим, что значительно меньшая сила, уравновешивает вес предмета. Как и почему это происходит? Проведем опыт. Нам уже известно, что на груз массой 102 грамма действует сила — вес тела 1 ньютон. Будем подвешивать грузы на различных расстояниях от точки опоры. При этом видно, что сила (F1) «эф» один вращает рычаг по часовой стрелке, а (F2) — против. Если грузы висят на одинаковых расстояниях, то рычаг находится в равновесии. Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует сила, называют плечом силы (указанное расстояние есть перпендикуляр). На рисунке они обозначены (l1) «эль» один и (l2 ) и «эль» два. Подвесим справа еще один груз, при этом сила (F1) «эф» один стала в два раза больше (2 Ньютона). Система вышла из равновесия. Сможет ли сила (F2) «эф» два уравновесить его? Увеличим плечо (l2) эль два, при увеличении плеча в два раза – рычаг снова в равновесии. Повторим этот же опыт, используя грузы весом 5 ньютонов и один ньютон. Опять замечаем, что при увеличении плеча в 5 раз рычаг приходит в равновесие.

На основании подобных опытов, было установлено правило равновесия рычага. Впервые это правило было сформулировано древнегреческим ученым Архимедом.

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. В виде формулы это правило записывается так: (), где (F1) «эф» один и (F1) «эф» два – силы, действующие на рычаг, (l1) «эль» один и (l2 ) и «эль» два — плечи этих сил

То есть меньшая сила уравновешивает большую при увеличении плеча силы во столько раз, во сколько отличаются силы.

Сила (F1) «эф» один больше силы (F2) «эф» два в два раза. Чтобы рычаг был в равновесии, плечо (l2 ) «эль» два должно быть в два раза длиннее, чем (l1) «эль» один.

Как вы думаете, почему ручку двери прикрепляют не к середине двери, а с краю? Чем больше плечо (расстояние от точки опоры до прямой, вдоль которой действует сила), тем меньше надо прикладывать усилий, чтобы открыть дверь.

Решим задачу. На меньшее плечо рычага действует сила 80 ньютонов, на большее — 20 ньютонов. Длина меньшего плеча 5 сантиметров. Определите длину большего плеча.

Запишем краткое условие. Обозначим большую силу F1, она равна 80 Ньютонов. Меньшую F2. Тогда меньшее плечо l1 переведем: 5 сантиметров – это 0,05 метра. Найти необходимо плечо l2. Запишем правило равновесия для рычага. Математически из этого равенства найдем неизвестное плечо l2. Подставляя числовые значения получаем ответ 0,2 метра или 20 см. Сделаем рисунок в соответствующем масштабе. Дано: F1 =80H F2 =20H l1 =5см СИ 0,05м Решение: Найти: l2 -?         Ответ:20см

Из рисунка видно, что сила меньшая в 4 раза может уравновесить большую при условии увеличения плеча меньшей силы также в четыре раза.

Не нашли, что искали? Воспользуйтесь поиском: