Кинематический анализ механизмов (аналитический и графический методы).

Кинематический анализ кривошипно-ползунного механизма

Аналитический способ

Дано

‑ длины звеньев

‑ частота вращения кривошипа

‑ положение кривошипа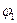

‑ положение В

Решение:

Графический способ

Кинематические характеристики кривошипно-ползунного (и любого другого) механизма могут быть определены и с помощью графоаналитического метода или как его чаще называют метода планов наложений скоростей и ускорений.

Планом механизма называется масштабное графическое изображение кинематической схемы механизма соответствующее заданному положению входного звена.

Планом скоростей механизма называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и направлению скоростям различных точек механизма в данный момент.

Чертёж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данный момент, называют планом ускорений механизма.

Построение плана механизма

Назначаем на плане механизма расстояние ОА (например ОА =50 мм), определяем масштабный коэффициент плана механизма.

Строим план механизма.

Из точки О откладываем под углом φ₁ отрезок длиной .

Откладываем горизонтальную прямую, отстоящую на расстоянии от точки О.

Из точки А делаем циркулем засечку радиусом на построенной горизонтальной прямой. Получаем точку В.

Построение плана скоростей

Ставим на плане скоростей полюс .

Точка А совершает вращательное движение. Определяем скорость точки A.

Скорость точки А направлена перпендикулярно кривошипу 1.

Задаемся на плане скоростей расстоянием 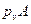. Определяем масштабный коэффициент для плана скоростей

Проводим из полюса вектор скорости длиной .

Строим скорость точки B.

Точка В принадлежит шатуну 2, совершающему плоскопараллельное движение.

Скорость точки В находится из равенства

Проводим из точки А линию перпендикулярную шатуну 2 , в сторону вращения .

Кроме этого точка В принадлежит ползуну 3, совершающему поступательное движение вдоль прямой :

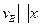
Проводим из полюса линию параллельную прямой х.

На пересечении этих линий будет находиться точка В.

Величина скорости точки будет определяться

Для определения угловой скорости звена 2 мысленно перенесем вектор скорости на план механизма и направляем угловую скорость в сторону вращения .

Модуль угловой скорости звена 3 определяем по формуле

Построение плана ускорений

Ставим на плане скоростей полюс .

Точка А совершает вращательное движение. Определяем ускорение точки A.

Т.к. = const = 0;

Задаемся на плане ускорений расстояние мм. Определяем масштабный коэффициент для плана ускорений

Откладываем из полюса вектор ускорения длиной 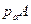от О₁ к А.

Точка В принадлежит шатуну 2, совершающему плоскопараллельное движение.

Кроме этого точка В принадлежит ползуну 3, совершающему поступательное движение.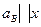

Определяем

Определяем величину этого вектора на плане ускорений

Откладываем из точки А вектор от В к А.

Величину вектора определить нельзя (неизвестно угловое ускорение ).

Проводим из полюса линию

На пересечении этих линий находится точка В.

Проводим вектор

Определяем величину ускорения точки В

Для определения углового ускорения звена 2 мысленно перенесем вектор на план механизма и направляем угловое ускорение в сторону вращения .

Модуль углового ускорения звена 2 определяем по формуле

Не нашли, что искали? Воспользуйтесь поиском: