
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
По выполнению контрольной работы № 1
В большинстве задач статики рассматривается равновесие тел, лишенных возможности перемещаться в направлении действия приложенных к ним активных тел. Тела, ограничивающие движение рассматриваемого тела, называются связями. Между телом и связью на основании закона равенства действия и противодействия возникают равные по модулю и противоположно направленные силы взаимодействия. Сила, с которой связь действует на рассматриваемое тело, называется реакцией связи или просто реакцией. Сила, с которой тело действует на связь, называется силой давления на связь. Таким образом, сила реакции и сила давления на связь - две равные по модулю силы, имеющие противоположное направление. Они приложены к разным телам.
Задачи на равновесие несвободных тел решают в такой последовательности: несвободное тело условно освобождают от связей, для чего связи мысленно отбрасывают, а вместо них к телу прикладывают реакции, эквивалентные действию связей на тело. Поскольку действующие на тело активные силы и силы реакций представляют уравновешенную систему тел, это дает возможность составлять уравнения равновесия, из которых определяют неизвестные реакции.
Задачи №№ 1-10
К решению задач №№1-10 следует приступать после изучения введения, темы 1.1 "Основные понятия и аксиомы статики" и темы 1.2 "Плоская система сходящихся сил", уяснения приведенных ниже методических указаний и разбора примера 1.
Во всех задачах рассматривается равновесие плоской системы сходящихся сил и требуется определить реакции двух шарнирно соединенных между собой стержней, удерживающих два груза. Таким образом, к шарниру В (рисунок 5) в каждой задаче приложены четыре силы, из которых две неизвестны. Для задач этого типа универсальным является аналитический метод решения.
Последовательность решения задач;
1 Выбрать узел, равновесие которого должно быть рассмотрено
(узел В).
2 Освободить узел В от связей, заменив их реакциями и изобразить действующие на него заданные силы и реакции отброшенных связей. Причем реакции стержней следует направлять вдоль их оси от шарнира В, предварительно считая стержни растянутыми.
3 Выбрать направление осей координат, совместив их начало с точкой В.
Решение можно упростить путем рационального выбора направления координатных осей. Одну из осей целесообразно направить перпендикулярно неизвестной силе, тогда ее проекция на эту ось будет равна 0.
4 Составить и решить уравнения, используя условия равновесия плоской системы сходящихся сил:
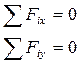
5 Проверить правильность полученных результатов графически.
Вспомним, что проекция силы на ось численно равна произведению модуля силы на косинус острого угла между линией действия силы и направлением оси координат. Знак проекции определяется и непосредственно по рисунку 4.
| Рисунок 4 |
Если направление от начала проекции к ее концу совпадает с положительным направлением оси, то берется знак "плюс". При обратном направлении - знак "минус"
Следует помнить, что проекция силы на ось не векторная, а скалярная величина.
Пример 1
Определить реакции стержней АВ и ВС кронштейна, удерживающего в равновесии груз F2 = 0,5 кН и растянутую пружину, сила упругости которой F1 = 0,3 кН. Весом частей конструкции, а также трением на блоке пренебречь. (Рисунок 5).

 | |||
 |
Рисунок 5
Решение
1 Рассматриваем равновесие шарнира В.
2 Освобождаем шарнир В от связей, заменяя их реакциями и изображаем действующие на него заданные силы и реакции связей. (Рисунок 6).
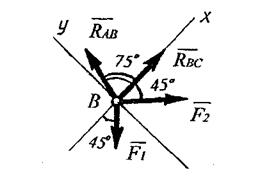
Рисунок 6
К точке В приложены заданные активные силы - сила натяжения троса BD, равная весу груза F2 и сила упругости пружины F1. Эти силы направляем от точки В, т.к. трос и пружина растянуты.
Рассматривая точку В, как свободную, отбрасываем связи (стержни АВ и ВС), заменяя их действие реакциями RAB и RBC.
Реакции стержней направляем от точки В вдоль их осей, т.к. предварительно полагаем стержни растянутыми. Если это предположение окажется неверным, то искомая реакция стержня получится в ответе со знаком "минус". Это говорит о том, что стержень сжат, а истинное направление реакции к точке В.
На узел В действует плоская система сходящихся сил. Полученная расчетная схема изображена на рис. 6.
3 Выбираем систему координат, совместив ось У по направлению с реакцией Rbc. Начало координат поместим в точке В. На узел В действует плоская система сходящихся сил.
4 Составляем и решаем уравнения равновесия для системы сходящихся сил, действующих на шарнир В.
Σ Fix = 0 _ алгебраические суммы проекций сил
системы на оси Х и У.
Σ Fiу = 0
4.1 Составляем уравнение проекций на ось У. Так как, совместив ось Х с реакцией RBC, в этом уравнении получим лишь одно неизвестное. Сила RBC не войдет в уравнение, т.к. она перпендикулярна оси У:
ΣFiу=0
-F1.cos45 ° -F2 .cos45° + RAB .cos150 = 0 
4.2 Спроецируем все силы на ось х:
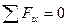 RBC + RAB . cos75° + F2 . cos45° - F] .cos45° = 0
RBC + RAB . cos75° + F2 . cos45° - F] .cos45° = 0
Rbc = -RAB .cos75° -F2 .cos45 ° + F1 .cos45° =
= -0,586 . 0,259 - 0,5. 0,707 + 0,3 . 0,707 = -0,293 kH
Решив систему уравнений, нашли, что
RBC = -0,293 кН и Rab = 0,589 кН.
Знак "минус" перед численным значением реакции Rbc показывает, что стержень ВС не растянут, как предполагалось, а сжат.
5 Для проверки правильности решения применяем графический метод.
Полученная система сил (рисунок 6) находится в равновесии, следовательно, силовой многоугольник, построенный для этой системы сил, должен быть замкнутым.
Строим силовой многоугольник в следующем порядке. (Рисунок 7).
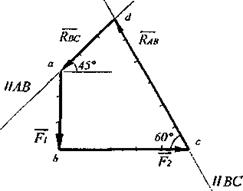
Рисунок 7
В выбранном масштабе (например, µсил = 0,1  )
)
От произвольной точки откладываем вектор заданной силы F1
(ab = F1), затем от конца вектора F1 - вектор заданной силы F2 (bс = F2).
Затем через начало вектора F 1, и конец вектора F2 проводим
известные направления искомых реакций стержней АВ и ВС. Эти прямые пересекаются в точке d. В результате построения образовался замкнутый многоугольник abсd, в котором сторона cd = RBC, а сторона ad = RAB.
Стрелки, изображающие направления сил RAB и RBC, ставим таким образом, чтобы в силовом многоугольнике было единое направление обхода (в данном случае против часовой стрелки).
Следует отметить, что силовой многоугольник показывает истинное, а не предполагаемое, направление искомых сил.
Измерив длины этих сторон в см и умножив на масштаб построения µсил, получаем значение реакций стержней:
RAB = ad . µсил = 6,0 . 0,1 = 0,6 кН,
RBС= cd.µcил =3,0.0,1 = 0,3 кН.
Вывод: графическое решение подтверждает правильность аналитического решения.
Точность графического метода тем выше, чем крупнее принят масштаб построения.
Задачи №№ 11 -20
К решению этих задач следует приступить после изучения темы 1.3 "Пара сил и момент силы относительно точки", темы 1.4 "Плоская система произвольно расположенных сил", уяснения приведенных ниже методических указаний и разбора примеров 2 и З.
Во всех задачах определению подлежат опорные реакции связей балки, находящейся в равновесии под действием плоской системы произвольно расположенных сил. Балки опираются на шарнирные опоры.
Последовательность решения задач:
1 Изобразить балку вместе с нагрузками.
2 Выбрать положение координатных осей и центров моментов:
- при выборе расположения осей координат удобно совместить ось Х
с осью балки;
-центры моментов целесообразно выбирать в точках пересечения
неизвестных сил.
3 Произвести необходимые преобразования заданных активных сил:
- силу F наклоненную к оси балки под углом 30° заменить двумя взаимно перпендикулярными составляющими Fx и FУ.
- равномерно распределенную нагрузку заменить ее равнодействующей, приложенной в середине участка распределения нагрузки.
4 Освободить балку от опор, заменив их действие реакциями, составляющие которых направить вдоль выбранных осей координат.
5 Составить и решить уравнения равновесия статики для плоской системы сил. Уравнения равновесия удобнее составлять, таким образом, и в такой последовательности, чтобы решением каждого из этих уравнений было определение одной из неизвестных реакций опор.
6 Проверить правильность найденных опорных реакций, решив уравнение, которое не было использовано для решения задачи.
Напоминаем, что моментом силы относительно точки называется произведение модуля силы на плечо, т.е. на длину перпендикуляра, восстановленного из точки, относительно которой берется момент (центра момента), на линию действия силы. Момент принято считать положительным, если он стремится повернуть тело по часовой стрелке (рисунок 8а), и отрицательным (рисунок 86), если его действие направлено в противоположную сторону.
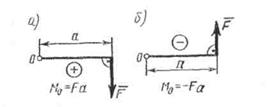
Рисунок 8
Следует обратить внимание на то, что момент силы относительно точки равен нулю в том случае, когда линия действия силы проходит через эту точку.
Нужно иметь в виду, что в отличие от момента силы, момент пары сил не зависит от положения этой пары сил на плоскости.
Решение задач можно упростить путем рационального выбора направления координатных осей и положения центров моментов.
Пример 2
Определить реакции опор балки, изображенной на рисунке 9а.

Рисунок 9
Решение
1 Изобразим балку, соблюдая заданные размеры ее участков и угла 30°. Рассмотрим равновесие балки под действием приложенных к ней нагрузок: силы F, равномерно распределенной нагрузки с интенсивностью q и пары сил с моментом М.
2 Начало координат поместим в точке А, ось Х совместим с осью балки. За центры моментов принимаем точки пересечения неизвестных сил, т.е. точки А и D.
3 Силу F заменяем ее составляющими Fx =F .cos30°Fy = F . cos 60. Равнодействующая равномерно распределенной нагрузки величиной q. 2 приложена в середине участка CD в точке К. (Рисунок 9б).
4 Освобождаем балку от опор, заменив их действие опорами реакциями (рисунок 9б). В шарнирно-подвижной опоре D реакция RDy направлена по перпендикуляру к опорной поверхности.
Величина и направление реакции шарнирно-неподвижной опоры А неизвестны. В этом случае реакцию RA заменяют двумя составляющими: вертикальной RAy и горизонтальной RAX. Теперь на балку действует плоская система произвольно расположенных сил.
5 Составляем три уравнения равновесия статики и определяем неизвестные реакции опор:
 ΣMA= 0 - алгебраическая сумма моментов всех сил относительно точки А
ΣMA= 0 - алгебраическая сумма моментов всех сил относительно точки А
ΣMD=0 - алгебраическая сумма моментов всех сил относительно точки D
ΣFix=0 - алгебраическая сумма проекций всех сил на ось х
5.1 ΣМА = 0
Fy.1+ M + q.2.3-RDy..4 = 0
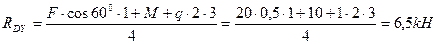

5.2 ΣMD = 0
Ray.4 – Fy.3 + M-q.2.1 = 0

5. 3 ΣFix = 0
Rax – Fx = 0
RAX = F . cos30° = 2 . 0,866 = 17,3 кН
6 Проверяем правильность найденных результатов, составив уравнение алгебраической суммы проекций всех сил на ось У:
ΣFiy = 0

Условие равновесия Σ Fjv = 0 выполняется, следовательно, реакции опор
найдены, верно.
Пример 3
Для балки, изображенной на рисунке 10а определить опорные реакции.

Рисунок 10
Решение
1 Рассмотрим равновесие балки АВ.
2 Начало координат поместим в точке А. За центры моментов принимаем точки А и В.
3 Равномерно распределенную нагрузку заменим равнодействующей q .2 (рисунок 10 б).
4 Освободим балку от связей, отбросив опоры и приложив вместо них неизвестные реакции (рисунок 10 б).
5 Для плоской системы параллельных сил достаточно двух уравнений равновесия

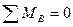

5.l ΣMA = 0; - М + F1 . 1,5 + q . 2 . 2,5 - F2 . 4,5 - RBy . 6 = 0
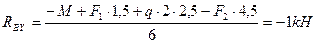
5.2 ΣMB = 0; Ray . 6 - M – F1 . 4,5 - q. 2. 3,5 + F2 . 1,5 = 0

Значение реакции RBy получено со знаком "минус". Это означает,
что она направлена вертикально вниз.
6 Для проверки правильности найденных реакций опор балки составляем уравнение алгебраической суммы проекций всех сил на ось У.
ΣFiy = 0; Ray – F1 – q.2 + F2+RBy = 11-10 – 4.2 + 8 + (-1) = 0
Следовательно RAy и RB y определены верно.
Задачи №№21-30
Эти задачи следует решать после изучения темы 1.7 "Центр тяжести" и внимательного разбора примеров 4 и 5.
В этих задачах требуется определить центры тяжести плоского составного сечения. Навыки определения центра тяжести плоских фигур необходимы для успешного решения многих практических задач в технике, например, при расчетах на прочность в задачах сопротивления материалов.
Последовательность решения задач:
1 Разбить составное сечение на простые элементы, для которых центры тяжести известны. К простым также относятся сечения профилей стандартного проката.
2 Определить площадь каждой простой фигуры.
3 Выбрать положение осей координат.
4 Определить координаты центров тяжести отдельных простых фигур относительно выбранных осей координат заданного плоского составного сечения.
5 Определить положение центра тяжести всего сечения по формулам:

где хс и ус — искомые координаты центра тяжести заданного составного сечения;
хi и yi; - координаты центров тяжести простых фигур, которые определяются непосредственно из заданных размеров;
Ai - площади простых фигур, которые определяются исходя из заданных размеров.
Пример 4
Для заданной плоской фигуры (тонкой однородной пластины) определить положение центра тяжести. Размеры даны на рисунке 11.
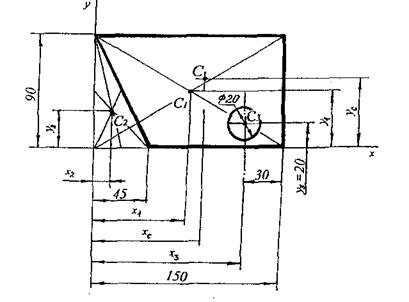
Рисунок 11
Решение
Определение положения центра тяжести фигуры означает определение координат этого центра. Расчеты ведем в сантиметрах.
1 Данную сложную фигуру представляем состоящей из трех простых:
1 - прямоугольник
2 - треугольник
3 - круг
2 Площадь прямоугольника без учета имеющихся в нем отверстий берем в расчете со знаком "плюс", а площадь круга и треугольника со знаком "минус".

3 Проводим оси координат так, чтобы все сечение было расположено в первом квадранте (координаты центров тяжести будут положительными).
4 Определяем координаты центров тяжести простых фигур:
Вспомним, что центр тяжести прямоугольника лежит на пересечении его диагоналей.

Центр тяжести треугольника лежит на пересечении его медиан. Расстояние от центра тяжести треугольника до его основания равно 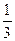 высоты.
высоты.
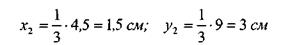
Определим координаты центра тяжести круга:
х3 = 15 - 3 = 12 см; уъ = 2 см
5 Координаты центра тяжести заданной фигуры определяем по формулам:
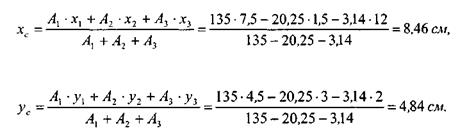
Центр тяжести С всего сечения показан на рисунке 11.
Пример 5
Для заданного сечения, изображенного на рисунке 12, составленного из приваренных друг к другу прокатных профилей, определить положение центра тяжести.
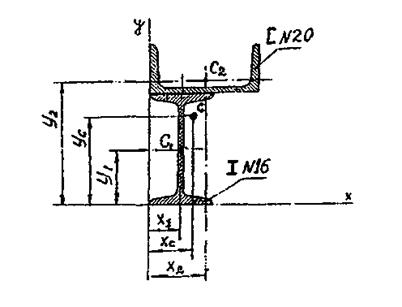
Рисунок 12
Решение
1 Данное сложное сечение представляем состоящим из двух
простых частей:
1 - двутавра № 16
2 - швеллера № 20.
Чертим сложное составное сечение в масштабе
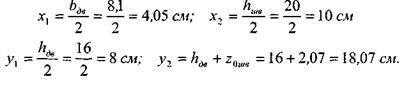
|
| 5 Центр тяжести всего сечения определяем по формулам: |
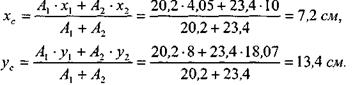
|
2Определяем площади простых частей. Площади двутавра и швеллера, берем из таблиц ГОСТа сортамента прокатной стали (приложения Б, В). Все расчеты ведем в сантиметрах, так как в таблицах ГОСТов на профили проката размеры даны в сантиметрах.
3 Проводим оси координат так, чтобы все сечение было расположено в первом квадранте.
4 Определяем координаты центров тяжести швеллера и двутавра:
Центр тяжести С всего сечения показан на рисунке 12.
При решении задач на определение центра тяжести начало системы координат целесообразно совмещать с центром тяжести одной из фигур. В этом случае расчеты значительно упрощаются.
Задачи №№31 -40
К решению задач кинематики следует приступить после изучения тем 1.8, 1.9, 1.10, 1.11, 1.12 и разбора примеров 6, 7, 8, 9.
Необходимо четко представлять, что такое скорость и ускорение движения точки, знать, какие существуют виды движения точки в зависимости от ускорения.
Ускорение - векторная величина, которая характеризует быстроту изменения скорости, как по модулю, так и по направлению.
Ускорение, характеризующее быстроту изменения числового значения скорости, называют касательным, а по направлению-нормальным.
Касательное ускорение аτ, всегда направлено по касательной
к траектории в рассматриваемый момент времени.
Если числовое значение скорости с течением времени остается неизменным, то касательное ускорение отсутствует. Это случай равномерного движения. Движение с постоянным касательным ускорением называется равнопеременным.
Нормальное ускорение ап всегда направлено по радиусу к центру кривизны траектории. Если точка движется прямолинейно, то скорость по направлению не меняется, значит, нормальное ускорение отсутствует.
При поступательном движении тела для решения задач применимы все формулы кинематики точки. Формулы для определения угловых величин характеризующих движение тела, вращающегося вокруг неподвижной оси, имеют вид, аналогичный формулам для определения соответствующих линейных величин поступательно движущегося тела. (Таблица 6).
Таблица 6
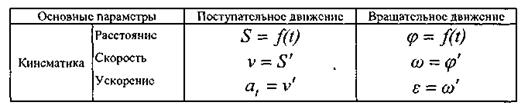
Для решения задач кинематики нужно использовать соответствующие готовые уравнения и формулы, выведенные в учебниках.
Решение задач следует иллюстрировать рисунками.
К решению задач динамики следует приступить после изучения тем 1.13, 1.14, 1.15, 1.16 и разбора примеров, 10, 11, 12, 13, 14.
Для того, чтобы успешно решить задачи по динамике необходимо разобраться в физическом смысле аксиом динамики, научиться использовать основанный на принципе Даламбера метод кинетостатики, который позволяет применять уравнения равновесия статики для тел, двигающихся с ускорением.
При этом не нужно забывать, что сила инерции прикладывается к телу, двигающемуся с ускорением условно и в действительности на него не действует.
Следует разобраться в физическом смысле понятий работы и мощности, изучить законы динамики для случаев поступательного и вращательного движения тел.
Так же, как в кинематике, в динамике между формулами для расчета поступательного и вращательного движений существует аналогия, иллюстрируемая таблицей 7.
Таблица 7
| Основные параметры | Поступа- тельное движение | Вращательное движение | |
| Динамика | Силовое воздействие Мера инертности Основной закон динамики Работа Мощность Кинетическая энергия | Сила F Масса m
F = т.а
W = F .S
P = F.v
Ek= 
| Момент М Динамический момент инерции J M = J.E W = М .φ Р = М. ω |
Пример 6
Поезд движется со скоростью υ = 50 км/ч по криволинейному участку пути радиусом R = 400 м. Определить ускорение поезда и пройденный путь за три минуты. (Рисунок 13).
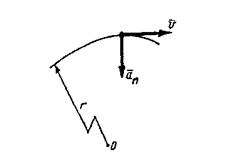
Рисунок 13
Решение
Движение поезда вдоль кривой осуществляется с постоянной скоростью υ = const, поэтому полное ускорение равно нормальному:
а = ап = 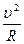 ;
;
υ = 50 км/ч = 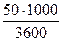 = 13,89 м/с,
= 13,89 м/с,
тогда 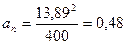 м/с2
м/с2
Определяем путь, пройденный поездом за t = 3 мин =180 с.
S|t=3 = v. t = 13,89 . 180 = 2500 м = 2,5 км
Пример 7
По кривой радиусом R = 1200 м движется поезд. Его скорость в начале движения составляет υo = 60 км/ч.
После того как поезд прошел расстояние 800 м, его скорость уменьшилась до 36 км/ч. определить полное ускорение в начале и конце движения.
Решение
Поезд совершает криволинейное равнозамедленное движение.
(Рисунок 14)

Рисунок 14
Определяем величину касательного ускорения из уравнений:

Из второго уравнения
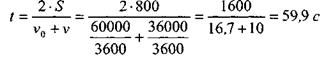
Из первого уравнения
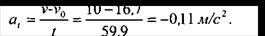
|
Так как движение равномерно замедленное, то касательное ускорение в течение всего времени движения постоянно. Найдем нормальное ускорение:
в начале движения: 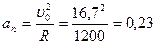 м/с2
м/с2
в конце движения  м/с2
м/с2
полное ускорение: в начале движения:

в конце движения:
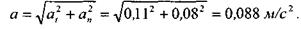
|
Пример 8
При равнопеременном движении точки по дуге окружности радиуса R = 500 м и на пути S = 1200 м ее скорость уменьшается с 30 до 10 м/с. Найти время движения и пройденный путь до полной остановки точки.

|
Рисунок 15
Решение
В задаче дано изменение скорости на пути S = 1200 м (рисунок 15). Ни из формулы пути, ни из формулы скорости непосредственно нельзя найти касательное ускорение или время этого движения.
Запишем обе формулы:
Из формулы (2) 
Подставим полученное выражение в (1) и выразим время t:
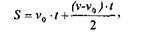
откуда

тогда
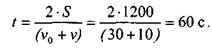
Найдем касательное ускорение

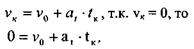
|
| откуда |
Вычислим время движения точки до полной остановки. Обозначим его tk
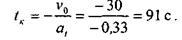
Пример 9
Колесо локомотива вращается так, что точка, лежащая на расстоянии 0,6 м от центра, движется по закону
S = 0,6. t + 0,2.t3 ( S - в метрах, t - в секундах). Найти для момента времени t = 3 с величину угловой скорости и углового ускорения (рисунок 16).
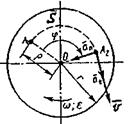
|
Рисунок 16
Решение
Определяем закон изменения скорости точки

Скорость точки в момент времени t1 = 3 с:
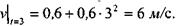
Угловая скорость тела в момент времени t1 = 3 с
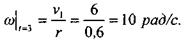
Закон изменения ускорения точки:

Касательное ускорение точки в момент времени t1 = 3 с:
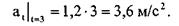
Угловое ускорение тела в момент времени t1 = 3 с:
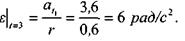
|
Пример 10
В момент выключения якоря тягового двигателя маховик имел частоту вращения п = 210 об/мин. Сколько оборотов сделал он до полной остановки при замедлении ε = 0,628 рад/с2? Какова продолжительность торможения?
Решение
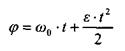
|
Маховик вращается равнозамедленно, его движение определяется уравнением
Уравнение угловой скорости имеет вид

В момент остановки ω= 0, следовательно:
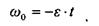
Выразим угловую скорость в рад/с
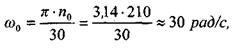
тогда 
Определяем угловое перемещение:

Зная, что один оборот, измеренный в радианах, выражается числом 2π, определяем число оборотов маховика до остановки:
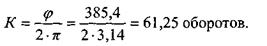
Пример 11
Мостовой кран опускает груз с начальной скоростью vo = 0,5 м/с и через t = 2 с останавливается. Вес груза 2500 Н. Определить в момент спуска натяжение R каната, к которому подвешен груз. Движение считать равнозамедленным.
Решение
На груз действуют следующие силы: вес груза, направленный вертикально вниз, и реакция каната, направленная вертикально вверх (рисунок 17).
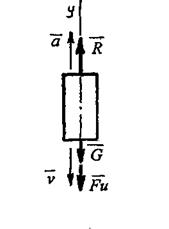
Рисунок 17
Приложим к грузу силу инерции Fu = m . а, направленную противоположно ускорению, т.е. вертикально вниз.
Воспользуемся принципом Даламбера. Из условия равновесия сил, действующих по одной прямой, имеем:
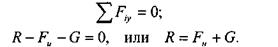
Из уравнения скорости равнозамедленного движения определим величину ускорения:
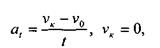
|
следовательно,

Определяем величину силы инерции:
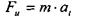
| Сила натяжения каната |
В эту формулу ускорение а, вводится по абсолютной величине, следовательно, имеем
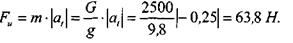
|
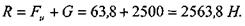
|
Пример 12
Определить, с какой постоянной скоростью автомобиль массой m = 2000 кг движется по выпуклому мосту, если в верхней точке моста сила давления автомобиля на мост составляет 11,6 кН. Радиус кривизны моста R = 100 м
Решение
Освободим автомобиль от связи и приложим к нему силу реакции моста. На основании закона равенства действия и противодействия сила реакции моста численно равна силе давления автомобиля на мост и противоположна ей по направлению, следовательно, R = 11,6 кН. На автомобиль действует активная сила - его сила тяжести G. Сила тяжести автомобиля и сила реакции не находятся в равновесии, так как автомобиль совершает криволинейное движение. (Рисунок 18).
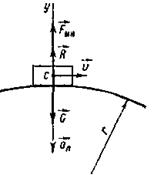
|
Рисунок 18
Двигаясь по мосту, автомобиль совершает равномерное криволинейное движение, при котором возникает лишь нормальное ускорение, направленное по радиусу к центру кривизны моста, а касательное - отсутствует. Воспользуемся принципом Даламбера и приложим к автомобилю кроме указанных сил еще силу инерции, направленную противоположно ускорению.
Схема сил, действующих на автомобиль, указана на рисунке 18.Все силы действуют по одной прямой, поэтому можно составить одно уравнение равновесия:
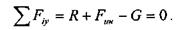
Выразим силу тяжести G и силу инерции Fин через массу автомобиля: G = m . g Fин= m . an
Вспомним, что 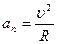 , тогда
, тогда 
Подставим полученные выражения в уравнение равновесия:
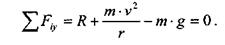
 Выразим из последнего уравнения скорость υ и определим её
Выразим из последнего уравнения скорость υ и определим её 
Пример 13
Найти силу, действующую в зацеплении зубьев шестерни и колеса, если диаметр шестерни d = 210 мм. Передаваемая мощность Р = 200 кВт при частоте вращения n = 1200 об/мин.
Решение
Мощность при вращательном движении определяется
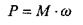
|
по формуле:
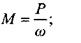
|

|
Так как

|
Искомая сила
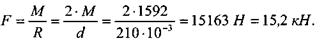
Пример 14
Поезд движется со скоростью 30 м/с по горизонтальному и прямолинейному участку пути. Завидев опасность, машинист начинает тормозить. Определить время до полной остановки и тормозной путь, если сила торможения равна 0,1 от веса поезда.
Решение
Приложим к поезду изображенному на рисунке 19 все действующие на него силы. На поезд действует неуравновешенная система сил. Сила тяжести G и сила реакции R уравновешивают друг друга, поэтому равнодействующая система сил равна силе торможения Ft. Воспользуемся теоремой об изменении количества движения и найдем время торможения. Импульс силы торможения условились считать отрицательным:
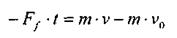
|

Рисунок 19
Нас интересует время движения до полной остановки, поэтому конечная скорость v = 0.
Но по условию сила торможения Ft = 0,1.G, а массу поезда можно выразить из основного закона динамики: G = m .g, откуда
 .
.
тогда 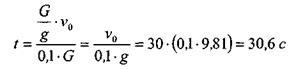
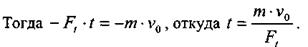
Для определения тормозного пути воспользуемся теоремой об изменении кинетической энергии, взяв работу силы торможения со знаком "минус":

Но υ = 0, тогда

откуда
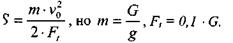
|
Тогда

Не нашли, что искали? Воспользуйтесь поиском: