
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Рассеяние шариков периодической решеткой
| Номер бросания, i | Координата ячейки xi, см | <x> - xi, см | (<x> - xi)2, см2 |
| - 3 - 8 - 21 - 6 | |||
| Среднее значение | - | - |
Заметим, что при использовании здесь и в следующих лабораторных работах программируемого калькулятора два последних столбца таблицы 10.1.1 являются излишними.
Приведенные в таблице 10.1.1 данные показывают, что движение шариков в решетке рассеивателей действительно непредсказуемо. Индивидуальные траектории, начинаясь в окрестности оси симметрии, заканчиваются то в левой, то в правой половинах установки. При этом отклонения траекторий иногда достигают очень большой величины: например, ячейки x 6 = 47 см и x 8 = 4 см. Однако непосредственно из таблицы 10.1.1 уловить какие-то закономерности обсуждаемого процесса довольно трудно. Значительно нагляднее эти закономерности проявляются, если отметить ячейки, в которые попали шарики, т. е. координаты xi концов траекторий, на числовой оси, как это сделано на рисунке 10.1.3, а. Напомним, что x в этой задаче – дискретная переменная, пробегающая значения от 1 до 48 см с шагом 1 см. Границы диапазона изменения x (ширина доски) показаны на рисунке 10.1.3 штриховкой. Здесь же вертикальной пунктирной линией изображено положение оси симметрии установки, т. е. абсцисса X начала всех траекторий.
Из рисунка 10.1.3 видно, что, во-первых, концы траекторий xi располагаются примерно симметрично относительно начальной точки X и, во-вторых, малые отклонения от оси симметрии наблюдаются значительно чаще, нежели большие. Замечательно также, что вычисленное по формуле 5.2.1 среднее значение номеров ячеек, в которые угодили шарики, <x> = 26, оказывается близким к абсциссе точки запуска. Подобное свойство случайно разлетающихся осколков снаряда, с учетом их масс, позволяет найти направление на орудие, выпустившее этот снаряд. Значение <x> показано на рисунке 10.1.3, а сплошной вертикальной черточкой. Здесь же круглыми скобками изображен доверительный интервал (<x> - D x, <x> + D x), вычисленный по формуле 8.3.1 с надежностью p = 0.95. Как видим, этот интервал охватывает большинство результатов таблицы 10.1.1.
Обработка данных таблицы 10.1.1 по методу Стьюдента дает
| x = (26 ± 8) см | (p = 0.95). | (10.1.1) |
Обсуждаемые закономерности случайного рассеяния частиц газа Лоренца проявляются еще нагляднее, если увеличивать число испытаний. На рисунке 10.1.3, б показано распределение по ячейкам 250 дробинок диаметром 2.0 мм. Экспериментальная установка, методика и условия опытов те же самые, что и в описанных ранее наблюдениях авторов за десятью частицами. Рисунок построен по сводным данным студенческой группы, каждый из членов которой

|
| Рис. 10.1.3. Рассеяние частиц периодической решёткой отражателей: а – результат 10 испытаний по данным таблицы 10.1.1. Прямоугольниками выделены ячейки, в которые попали шарики; б – результат 250 поочередных испытаний. По вертикальной оси отложено количество шариков, угодивших в соответствующую ячейку. На одну частицу приходится столбик такой же высоты, как на фрагменте а; в – результат 500 поочередных испытаний. Линия 1 – одна частица изображается таким же столбиком, как на фрагментах а и б; линия 2 – столбиком вдвое меньшей высоты; г – распределение по ячейкам при засыпке нескольких десятков тысяч шариков |
запускал на решетку одну за другой 10 своих дробинок. Координаты xi из таблицы 10.1.1 также учтены в этом массиве данных. На рисунке 10.1.3, б уже угадывается функция распределения (8.2.3): гистограмма 10.1.3, б имеет максимум вблизи оси симметрии доски, то есть вблизи абсциссы X точки бросания, примерно симметрична относительно этой оси, а ее ветви спадают с удалением от X подобно «хвостам» функции распределения Гаусса (8.2.3), представленной кривой 4 на рисунке 8.1.1. Увеличение числа частиц в крайних карманах объясняется отражением шариков от узких боковых границ используемой экспериментальной установки. Однако диаграмма 10.1.3, б еще далека от плавной кривой, поскольку на ней имеется большое количество провалов и выступов значительной величины.
В разделе 8.1 указывалось, что для приближения к гладкой кривой распределения следует увеличивать число испытаний до бесконечности. Чтобы проиллюстрировать изменения, происходящие с гистограммой при таком предельном переходе, на рисунке 10.1.3, в изображена диаграмма распределения 500 частиц. Для ее построения, кроме данных для 250 шариков, приведенных на рисунке 10.1.3, б, использовались результаты еще одной студенческой группы, полученные по такой же методике и с тем же количеством шариков. Если, независимо от количества испытаний, попадание шарика в ячейку отмечать столбиком одной и той же высоты, площадь, заключенная между ломаной и осью абсцисс, будет возрастать пропорционально числу измерений. В нашем случае площадь диаграммы для пятисот шариков будет ровно в два раза больше, чем для двухсот пятидесяти (рисунок 10.1.3, в, линия 1). Зависимость площади гистограммы, а вместе с ней максимальной ординаты и высоты ступенек, от числа измерений затрудняет сопоставление диаграмм и понимание закономерностей их эволюции. Поэтому, как отмечалось в разделе 8.1, существует договоренность: при построении гистограмм и функций распределения использовать такой вертикальный масштаб, чтобы ограничиваемая ими площадь была неизменной (и численно равной единице). В нашем примере с пятьюстами и двумястами пятьюдесятью шариками это условие легко соблюсти, если во втором случае отмечать попадание шарика столбиком вдвое меньшей высоты. В таком масштабе диаграмма распределения пятисот частиц представлена на рисунке 10.1.3, в линией 2. Теперь легко увидеть, что гистограммы для этих двух серий испытаний качественно подобны. В то же время, при большем количестве измерений число крупных скачков на диаграмме и размах этих скачков заметно уменьшаются.
Эта тенденция проявляется еще отчетливее, если выполнить опыты с тысячами или десятками тысяч частиц. Однако, если проводить такие опыты по прежней методике, запуская на решетку каждый шарик в отдельности и наблюдая его движение, понадобятся очень большие затраты времени и сил. Поэтому будем насыпать шарики в установку через воронку «непрерывным потоком» до тех пор, пока одна из ячеек не заполнится ими доверху. В нашей установке с карманами сечением 1.0 см2 и высотой 14 см и с шариками диаметром 2.0 мм в один лишь доверху заполненный карман поместятся около двух с половиной тысяч частиц. Чтобы не иметь дела с подсчетами большого количества частиц, скопившихся в каждой из ячеек, учтем, что плотность упаковки, то есть количество шариков в единице объема, во всех ячейках примерно одинаковы. Поэтому высота столба шариков в той или иной ячейке прямо пропорциональна числу частиц, оказавшихся в ней. Следовательно, при насыпании большого количества частиц мы получаем непосредственно гистограмму их распределения по ячейкам. Другими словами, установка «сама строит гистограмму»! Пример такой гистограммы приведен на рисунке 10.1.3, г, по вертикальной оси которого отложены высоты столбов из шариков, зарегистрированные в одном из опытов. Максимальная ордината соответствует высоте кармана (14 см). Масштаб по вертикали выбран из условия, чтобы площадь этой диаграммы была такой же, как на рисунках 10.1.3, б и 10.1.3, в, линия 2. Мы видим, что эта гистограмма остается подобной диаграммам, полученным для меньшего числа частиц. В то же время, она составлена из значительно меньших ступенек и поэтому существенно точнее приближается к плавной кривой распределения Гаусса (8.2.3). Для более лучшего приближения нам следовало бы не только увеличивать число испытаний, но и устремить к нулю ширину интервалов (ячеек). Однако здесь мы ограничены возможностями экспериментального метода, поскольку ширина карманов не может быть намного уменьшена – в частности, карманы не могут быть уже частиц.
В заключение подчеркнем достоинства методики Стьюдента для отыскания истинного значения случайной величины (в нашем примере – абсциссы X точки запуска шариков) и доверительного интервала (<x> - D x, <x> + D x) с помощью малого числа измерений. Действительно, сравнивая рисунки 10.1.3, а – 10.1.3, г, замечаем, что среднее значение <x>, найденное по результатам всего десяти бросаний, отличается от истинного значения X в такой же мере, как в сериях из сотен или даже десятков тысяч испытаний. Сопоставление этих рисунков показывает также, что доверительный интервал, вычисленный по данным десяти наблюдений, охватывает большую долю результатов даже очень длинных серий измерений.
Измерени я
· Каждый из студентов группы запускает поочередно десять шариков на решетку рассеивателей доски Гальтона, наблюдает их движение и записывает в таблицу, подобную таблице 10.1.1, координаты xi ячеек, в которые попали шарики.
· По десяти своим наблюдениям xi студент вычисляет по формулам методики Стьюдента 5.2.1 и 8.3.1 среднее значение <x> и доверительный интервал (<x> - D x, <x> + D x) и записывает результаты в виде выражения 2.1.1.
· Далее, подобно тому, как это сделано на рисунке 10.1.3, а, на числовой оси отмечаются начальная абсцисса X всех траекторий, их конечные координаты xi, значение <x> и доверительный интервал(<x> - D x, <x> + D x).
· На основании наблюдений, таблицы и рисунка делаются выводы о том, является или нет движение шарика в периодической решетке случайным, а также о том, попадает или нет истинное значение координаты точки запуска X в найденный в опытах доверительный интервал. Эти выводы записываются в тетрадь.
· Затем такие же вычисления проделываются с четырьмя произвольно выбранными из таблицы значениями xi, например, x1, x2, x3, x4, и получаются какие-то другие <x> и D x. Строится еще один рисунок, на котором на числовую ось наносятся выбранные координаты xi и результаты их обработки. Полученные данные сопоставляются с результатами десяти испытаний и объясняются причины их сходства или отличия.
Следующее задание состоит в построении гистограммы по данным наблюдений всей студенческой группы, т. е. ориентировочно для двухсот пятидесяти частиц (см. рисунок 10.1.3, б). Для этого на большом листе ватмана или миллиметровой бумаги рисуется горизонтальная ось с крупными (например, по 1 см на одну ячейку) делениями. Каждый студент отмечает попадания своих десяти частиц, закрашивая карандашом или фломастером соответствующие ячейки столбиками определенной высоты – скажем, в 0.5 или 1 см на одну частицу. Построение начинается от дна карманов, т. е. от горизонтальной оси. Получившаяся в итоге верхняя граница столбиков выделяется яркой линией. Продолжением этого задания может быть объединение данных нескольких студенческих групп, что позволит проиллюстрировать эволюцию гистограммы по мере увеличения числа испытаний с 250 до 500, затем до 750 и т. д. Для этого каждая следующая группа наносит свои данные поверх распределения, построенного предыдущей группой.
Затем всей группой выполняется опыт с засыпкой большого количества шариков. Если позволяет время, такой опыт повторяется несколько раз. Это помогает убедиться в том, что конкретные реализации случайного процесса в деталях могут отличаться одна от другой положением максимума, уровнями шариков в ячейках. В то же время во всех реализациях сохраняются общие закономерности - гистограммы напоминают распределение Гаусса (8.2.3), примерно симметричны относительно вертикальной оси, и их максимум располагается недалеко от этой оси. После этого каждый студент переносит в свою тетрадь гистограмму распределения двухсот пятидесяти частиц, а также «реальную» гистограмму непосредственно с доски Гальтона.
Для удобства сравнения целесообразно разместить эти гистограммы, а также рисунки с десятью и четырьмя частицами на одном листе бумаги друг под другом, как это сделано на рис. 10.1.3. Кроме того, следовало бы позаботиться о том, чтобы площади гистограмм были одинаковыми. Однако выполнение этого условия потребовало бы от нас тщательных подсчетов, неоправданных при нашем полуколичественном, иллюстративном уровне рассмотрения. Поэтому ограничимся приближенным условиям, чтобы максимумы обеих гистограмм имели одинаковую высоту.
Имея такой рисунок, следует сопоставить гистограммы между собой и с гауссовой кривой (8.2.3); количество и высоту выступов и провалов на них; положение их максимумов в сравнении с координатой X начала траекторий; долю результатов, попадающих в доверительные интервалы, найденные по данным десяти и четырех испытаний.
Контрольные вопросы к работе 10.1
1. При построении гистограмм 10.1.3, а – 10.1.3, в были использованы результаты опытов с отдельными, не взаимодействующими друг с другом дробинками. Гистограмма 10.1.3, г построена при насыпании дробинок «потоком», когда они могут «мешать» друг другу во время движения. Можно ли в таком случае сопоставлять как идентичные эти гистограммы?
2. В экспериментальной установке диаметр дробинок (2.0 мм) и диаметр гвоздей-рассеивателей (1.0 мм) были одного порядка. Можно ли в таком случае утверждать, что в данной работе моделируется газ Лоренца – рассеяние материальных точек на кругах конечного диаметра?
3. Гвозди на доске Гальтона расположены в шахматном порядке. Что произойдет, если их расположить хаотическим образом, оставляя, однако, в силе условие, по которому на каждой единице площади доски должно находиться в среднем одинаковое число рассеивателей?
4. В этом опыте истинное значение X известно. Всегда ли это бывает? Приведите пример, когда X неизвестно.
5. На использованной нами доске Гальтона размещался 41 горизонтальный ряд рассеивателей. Как будет меняться вид гистограмм 10.1.3, г при увеличении и уменьшении числа рядов? Останется ли гауссовым распределение шариков по карманам при таких изменениях экспериментальной установки?
6. При распределении тепла в теле быстрые, уже «нагревшиеся» молекулы сталкиваются с более медленными, передавая им свои импульс и энергию. Таким образом, механизм теплопроводности в чем-то похож на процесс рассеивания дробинок на доске Гальтона. Правомочна ли такая аналогия? Можно ли на основании этого сопоставления утверждать, что распределение частиц в карманах доски Гальтона 10.1.3, г является дискретным аналогом непрерывного распределения температуры, например, в стержне, к которому в точке X на некоторое время поднесли горящую свечу? Изменению каких параметров доски Гальтона будет в таком случае соответствовать увеличение времени между нагревом стержня и определением в нем распределения температуры? Приведите еще какие-либо физические процессы, которые можно промоделировать на доске Гальтона.
7. Раскрутив мысленно рисунок 10.1.3, г вокруг вертикальной оси, проходящей через точку X, представим себе «заметенный» при этом объем. Предложите установку, на которой можно было бы получить такое двухмерное распределение. Запишите соответствующую функцию распределения по аналогии с формулой (1.1.4).
8. Как зависит форма кривой 10.1.3, г от начальных условий: ширины отверстия в воронке, из которой насыпаются шарики, наклона воронки, скорости вылета из нее дробинок? Можно ли, в принципе, провести эксперимент так, чтобы получить не гауссово, а прямоугольное распределение, когда все дробинки соберутся, например, в 24 и 25 карманах и ни одна частица не попадет в другие ячейки?
9. Можете ли Вы предложить технологически более простую модель для изучения статистических закономерностей?
10.2. ЛАБОРАТОРНАЯ РАБОТА
Экспериментальное определение числа π.
Игла Бюффона
Принадлежности: лист миллиметровой бумаги и тонкий стержень – проволочная спица, иголка, спичка, карандаш, авторучка и т.д.
Для опытного определения приближенного значения числа π Бюффоном был предложен эксперимент, в котором на горизонтальную плоскость, разграфленную на квадратные клетки вертикальными и горизонтальными прямыми, отстоящими друг от друга на расстоянии 2 а (см. рисунок 10.2.1), наудачу, т. е. случайным образом, бросается игла длиной 2 l (l > 0).
Обозначим через mi число прямых, которые пересекает и которых касается игла при i -ом бросании. В приведенном на рисунке 10.2.1 примере mi = 14: семь горизонтальных и семь вертикальных линий.

|
| Рис. 10.2.1. Схема эксперимента по определению числа π |
Авторы провели опыты с миллиметровой бумагой и шариковой авторучкой длиной 2 l = 13.7 см, подсчитывая числа пересечений сантиметровых делений (2 а = 1.00 см). Результаты одного из опытов приведены в таблице 10.2.1.
Таблица 10.2.1 (29.04.2003)
Данные для определения числа π
Масштабно-координатная бумага 2 а = 1.00 см
Шариковая ручка длиной 2 l = 13.7 см
| Номер бросания i | Число пересечений mi, безразмерно | Число π, безразмерно | <π> - πi | (<π> - πi)2 |
| 2.88 3.42 3.22 2.88 2.74 | - 0.13 0.41 0.21 - 0.13 - 0.27 | 0.017 0.168 0.044 0.017 0.073 | ||
| Среднее | - | 3.03 | - | - |
Число π находится по формуле [10, 11]:
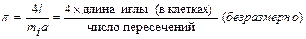 . .
| (10.2.1) |
Обоснование этой формулы дается в конце описания данной лабораторной работы.
Обработка данных таблицы 10.2.1 по Стьюденту (формулы (5.2.1) и (8.3.1)) дает
| π = 3.05 ± 0.35 ≈ 3.0 ± 0.4 | (p = 0.95). | (10.2.2) |
Для наглядности нанесем на числовую ось точками каждый из приведенных в таблице 10.2.1 результатов πi (рисунок 10.2.2, а). Среднее значение <π> отметим сплошной вертикальной чертой, а доверительный интервал (<π> - D π, <π> + D π) покажем круглыми скобками. «Истинное» значение числа π = 3.1415… изобразим вертикальной пунктирной линией. Обратим внимание, что, в соответствие с определением доверительного интервала как интервала, в который при p = 0.95 попадает 95 % всех результатов (строго говоря, при очень длинной серии испытаний), вне скобок на рисунке 10.2.2, а располагается всего одна экспериментальная точка.

|
Рис. 10.2.2. Результаты измерений числа π:
а – экспериментальные точки, среднее и истинное значения, доверительный интервал по данным таблицы 2.2.1;
б – гистограмма данных таблицы 10.2.2. По вертикали отложено количество экспериментальных точек, попавших в интервал. Максимальная ордината отвечает 18 попаданиям, а минимальная отличная от нуля ордината – одному попаданию
Из числовой записи экспериментальных результатов (10.2.2) и диаграммы рисунка 10.2.2, а видно, что в нашем случае «истинное» значение числа π попадает в найденный в опытах доверительный интервал. В отчетах, статьях и других научных сообщениях этот вывод принято формулировать примерно такими словами: «В пределах погрешности эксперимента приведенный результат согласуется с табличными данными (данными других авторов, результатами теоретических расчетов и т.д.)».
Как обсуждалось в разделе 8, метод Стьюдента применим лишь для случайных величин, распределения которых близки к распределению Гаусса (8.2.3). Поэтому, вообще говоря, прежде чем использовать формулы Стьюдента (5.2.1) и (8.3.1) для обработки результатов эксперимента, следует убедиться, что даваемые этим экспериментом результаты удовлетворяют такому условию. Сделать это можно, проведя достаточное количество измерений и сравнив их гистограмму с гауссовой кривой. Чтобы показать, что результаты измерений числа π с помощью бросаний иглы удовлетворяют названному требованию, авторы выполнили 100 измерений, включая пять приведенных выше. Распределение результатов на числовой оси дается в таблице 10.2.2.
Таблица 10.2.2 (1.05.2003)
Результаты измерений числа π
| Интервал числовой оси | 2.40 – 2.50 | 2.50 – 2.60 | 2.60 – 2.70 | 2.70 – 2.80 | 2.89 – 2.90 | 2.90 – 3.00 | 3.00 – 3.10 | 3.10 – 3.20 |
| Количество наблюдений |
Продолжение таблицы 10.2.2
| Интервал числовой оси | 3.20 – 3.30 | 3.30 –3.40 | 3.40 – 3.50 | 3.50 – 3.60 | 3.60 – 3.70 | 3.70 – 3.80 | 3.80 – 3.90 |
| Количество наблюдений |
Всего 100 бросаний.
При подсчетах точка, приходившаяся на левую границу интервала, включалась в него, а попадавшая на правую границу – исключалась и учитывалась в следующем интервале. (При такой договоренности отрезок обозначают символом [) и называют закрытым слева и открытым справа). Например, точка π = 3.10 включалась в интервал π = [3.10; 3.20), а точка π = 3.20 – в интервал π = [3.20; 3.30).
В графическом виде распределение результатов таблицы 10.2.2 представлено на рисунке 10.2.2, б. Полученную гистограмму можно рассматривать как приближение (правда, весьма грубое) кривой распределения Гаусса. Для более точного сравнения требуется во много раз большее количество измерений. Тем не менее, уже на основании имеющихся данных можно с уверенностью утверждать, что метод Стьюдента применим для определения среднего и оценки погрешности в нашем эксперименте. Обратим также внимание на то, что максимум гистограммы приходится на окрестность истинного значения числа π, а основная доля из ста экспериментальных данных укладывается в доверительный интервал для погрешности, найденный с помощью всего десяти измерений (рисунок 10.2.2, а).
Измерения
Каждый из студентов кладет перед собой горизонтально лист масштабно-координатной бумаги и определяет с точностью до миллиметра длину 2 l стержня, используемого им в качестве Иглы Бюффона. Чтобы точность измерений была не ниже двух значащих цифр, необходимо, чтобы длина стержня была более 10 мм и число пересекаемых линий более десяти. Поэтому для короткой иглы подсчитывается число пересечений с миллиметровыми делениями бумаги и полагается 2 а = 1 мм. Если игла длиннее 10 см, учитываются лишь сантиметровые графы и принимается 2 а = 1 см. Выполняется 10 бросаний, причем прослеживается, чтобы ориентации стержня при бросаниях отличались одна от другой. Результаты записываются в таблицу, составленную по образцу таблицы 10.2.1. Кроме того, четыре произвольно выбранных значения, например, π2, π4, π7 и π9, каждый студент заносит в сводную таблицу на аудиторной доске. Если в группе 25 человек, то банк данных будет содержать 100 чисел, что вполне достаточно для получения гистограммы. В первую очередь следует убедиться, что результаты измерений образуют случайную последовательность, для обработки которой применим метод Стьюдента. Чтобы выяснить это, нужно построить гистограмму по данным сводной таблицы. С этой целью на оси абсцисс выделите диапазон, в который попадают все 100 экспериментальных данных. Разбейте этот диапазон на равные отрезки, выбрав их так, чтобы количество отрезков было не менее десяти, а их длина была удобной для подсчетов и построения. В разобранном выше примере при разбросе результатов измерений в диапазоне 2.4 < π < 3.9 последний был разделен на 15 отрезков длиной 0.1. Дробление массива из ста чисел на существенно большее количество интервалов нецелесообразно, так как в такие интервалы будет попадать слишком мало точек. Подсчитайте число экспериментальных значений πi, приходящихся на каждый из выбранных Вами отрезков. При этом условьтесь учитывать точки, совпадающие с границами между отрезками, к примеру, так, как это сделано при составлении таблицы 10.2.2. Составьте таблицу, подобную таблице 10.2.2, и впишите в нее результаты этих подсчетов. Число попаданий в каждый из интервалов отложите в удобном масштабе по оси ординат (смотри рисунок 10.2.2, б). Сравните полученную гистограмму с кривой распределения Гаусса (8.2.3). Сделайте вывод о применимости метода Стьюдента для обработки результатов данного эксперимента.
Далее по десяти своим измерениям (см. таблицу 10.2.1) вычислите среднее значение <π> и погрешность D π по формулам Стьюдента (5.2.1) и (8.3.1), запишите результаты в форме (10.2.2), приведите их на числовой оси, как это сделано на рисунке 10.2.2, а, и сделайте вывод о том, согласуются или нет данные Вашего эксперимента с табличным значением числа π.
Затем это же самое проделайте по четырем измерениям, занесенным в общую таблицу на доске. При этом получится какое-то другое <π> и новое D π. Сравните их с прежними величинами и проанализируйте разницу.
Сопоставьте положение максимума гистограммы с табличным значением числа π и найденными Вами по результатам десяти и четырех измерений средними значениями <π>, а ширину гистограммы – с доверительными интервалами (<π> - D π, <π> + D π). Для этого полезно расположить гистограмму и рисунки, на которых показаны Ваши десять и четыре экспериментальные точки, на одном листе бумаги друг под другом, как на рисунке 10.2.2. Все выводы запишите в тетрадь.
Не нашли, что искали? Воспользуйтесь поиском: