Достаточность принципа максимума

Пусть X – конечномерное пространство, Y X – подпространство, A: X→X – линейное преобразование. Будем говорить, что Y – подпространство инвариантное относительно A, если A(Y) Y. Когда Y ≠X, то Y – собственное подпространство. Пусть a 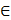X. Элемент a принадлежит собственному инвариантному подпространству Y тогда и только тогда, когда вектора {a,Aa,…,A^k-1a} линейно зависимы, что очевидно, так как из независимости этой системы следует, что подпространство Y совпадает с X.

Будем говорить, что для задачи быстродействия выполнено условие общности положения, если для каждого вектора w параллельного некоторому ребру многогранника U, вектор Bw не принадлежит никакому собственному инвариантному подпространству A, то есть вектора {Bw,ABw,…,A^k-1Bw} образуют линейно зависимую систему.

Замечание 1. Множество векторов, для которых det{Bw,ABw,…,A^k-1Bw}≠0, является нигде неплотным. Следовательно, добиться выполнения условия общности положения можно всегда сколь угодно малым сдвигом. Множество называется нигде неплотным, если его дополнение всюду плотно.

Лемма 4. Пусть P(t) – нетривиальное решение сопряженной системы = - PA, a ≠0 такое, что P(τ)a=0 для всех τ 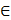(τ₀, τ₁). Тогда a принадлежит некоторому собственному инвариантному подпространству относительно преобразования А.

Теорема 3. Пусть u(t) – допустимое управление, заданное на отрезке [t₀, t₁], x(t) – соответствующая траектория, удовлетворяющая начальным условиям x(t₀)=x₀ и x(t₁)=0. Тогда для оптимальности управления необходимо и достаточно, чтобы оно удовлетворяло принципу максимума.

Теорема 4 (о конечности переключений). Для любого нетривиального решения P(t) сопряженной системы = - PA соотношение P(t)Bu(t) = однозначно определяет управление u(t). Кроме того, управление u(t) оказывается кусочно-постоянным и его значениями являются лишь вершины многогранника U.

Теорема 5. Пусть U={u: a^β ≤ u^β ≤ b^β, β=1,…,r}, собственные значения матрицы A – вещественные. Тогда в оптимальном управлении u(t) =(u¹(t),…,u^r(t)) каждая функция u^β(t) кусочно-постоянна, принимает лишь значения a^β, b^β, и имеет не более (n-1) точек переключения.

Не нашли, что искали? Воспользуйтесь поиском: