Плотность вероятности для энергии системы, описываемой каноническим распределением Гиббса.

Запишем каноническое распределение:

Выразим константу через свободную энергию:

, а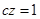

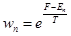
Мы писали:

- сумма по всем состояниям.

Проведя суммирование, получим , т.е. энтропия определяется по наиболее вероятному состоянию.

Вообще, исходя из :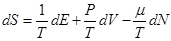

Но мы записали только один параметр:

Переходим в квазиклассику:

- это плотность вероятности реализации состояния 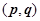. Переходим от суммирования к интегрированию:

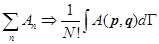, где

Для суммы - номер состояния, для интеграла - число степеней свободы()

Часто представляет интерес получение функции распределения энергии системы.

Точка в квазиклассике не характеризует состояние, а состояние характеризует фазовый объём:

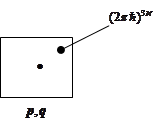Для описания распределения энергии введём функцию . У нас теперь - непрерывная величина. Тогда имеем:

Тогда: , здесь подразумевают интегрирование и сведение к полученному выражению.

- т.е. имеет место интегрирование.

Мы писали, что можем сделать замену интеграла на некое среднее и такие что:

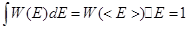
Мы писали, что:

Тогда имеем:

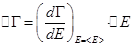- это как статистический вес

Таким образом мы кривую заменили на прямоугольник:

Оценка даёт:

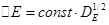
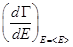- есть некая функция от

Вывод:

, - это функция от среднего значения энергии , т.е.:

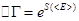
Так как энтропия - это функциональная зависимость, то можем перейти от к произвольной , т.е. от переходим к . Мы рассматриваем функциональную зависимость энтропии от переменной энергии:

Можем двигать по оси энергий и смотреть что это даёт.

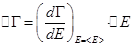Имея соотношение , получаем:

Здесь зависимость от - некая аналитическая связь.

Нам нужно оценить число состояний в интервале энергий .

Тогда:

В этом разложении дальше слагаемые не учитываем – их учёт даёт поправку к Гауссовому закону для . Учёт до третьего слагаемого приводит к Гауссовому закону для .

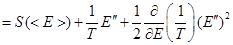
Показатель экспоненты имеем в виде:

, где

Мы получили Гауссов закон распределения. Это есть приближенная аппроксимация, т.к. не учитываем остальных членов в разложении энтропии в ряд.

Не нашли, что искали? Воспользуйтесь поиском: