Однородные уравнения. Однородные ДУ 1-го порядка имеют вид:

Однородные ДУ 1-го порядка имеют вид:

(4)

Это уравнение сводится к уравнению с разделяющимися переменными при помощи замены где Действительно, подставляя в уравнение (4) 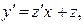получаем: — уравнение с разделяющимися переменными. Разделяя переменные, получим

После вычисления интеграла вместо z нужно подставить и, если можно, упростить полученное выражение.

Пример Найти общее решение ДУ

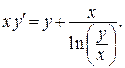
Решение. Разделим уравнение на (х = 0 не принадлежит ООУ) и получим: — однородное уравнение вида (4) в котором

Делаем замену 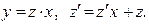Тогда исходное уравнение становится уравнением с разделяющимися переменными:

Найдем интегралы в левой и правой частях полученного равенства:

Итак, получим:

— общий интеграл исходного ДУ.

Линейные уравнения

Линейные ДУ 1-го порядка имеют вид:

(5)

где p (x) и q (x) — известные функции, непрерывные на некотором интервале.

Такие уравнения обычно решают методом Бернулли, который состоит в следующем. Решение ищется в виде произведения двух функций 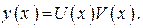Тогда Подставляя y и в (5), получим:

Объединим второе и третье слагаемые в левой части последнего уравнения, вынося U за скобки, и получим:

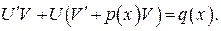(6)

Поскольку одну неизвестную функцию у заменили двумя функциями U и V, то одну из этих функций можем взять произвольно. Выберем функцию V (x) так, чтобы она была решением уравнения

(7)

тогда вторая функция U (x) должна удовлетворять уравнению

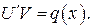(8)

Решив уравнение с разделяющимися переменными (7), найдем V и подставим его в (8), откуда найдем U. Общее решение получим как произведение найденных функций U и V:

Пример. Найти общее решение ДУ:

Решение. Уравнение имеет вид (5), поэтому является линейным. Решим его методом Бернулли. Сделаем замену

Приравняем коэффициент при U к нулю и получим:

Решим первое из полученных уравнений:

(при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение.

Полученную функцию подставим во второе уравнение:

(использовали формулы 2 и 7 таблицы интегралов).

Таким образом, или 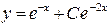— общее решение исходного ДУ.

Уравнения Бернулли

Уравнения Бернулли имеют вид:

(9)

где

Метод решения таких уравнений тот же, что и для линейных уравнений.

Пример. Найти общее решение ДУ:

Решение. Разделим уравнение на (х = 0 не является решением данного ДУ):

Полученное уравнение имеет вид (9), следовательно, это уравнение Бернулли. Сделаем замену Получим:

Приравняем коэффициент при U нулю и получим:

Решим первое уравнение:

(использовали формулу 4 таблицы интегралов).

Подставим полученную функцию V во второе уравнение:

(использовали формулы 3 а и 9 таблицы интегралов).

Таким образом, общее решение ДУ:

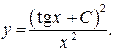
Случай V = 0 и 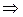y = 0 является решением ДУ, и так как оно не может быть получено из общего решения, то является особым решением.

Все рассмотренные типы ДУ 1-го порядка и методы их решения включены в таблицу ДУ 1-го порядка (см. прил. 2).

Не нашли, что искали? Воспользуйтесь поиском: