Элементарная поверхность. Определение 3.1. Область на плоскости называется элементарной областью, если она является образом открытого круга при гомеоморфизме

Определение 3.1. Область на плоскости называется элементарной областью, если она является образом открытого круга при гомеоморфизме, т.е. при взаимно однозначном и непрерывном отображении.

Таким образом, внутренность квадрата, прямоугольника, эллипса – всё это элементарные области.

Пусть Ф – элементарная поверхность и G – элементарная область на плоскости, являющаяся образом Ф при гомеоморфизме.

Определение 3.2. Поверхностью F в пространстве называется множество точек пространства, которое можно покрыть конечным или счётным множеством элементарных поверхностей.

Из этого определения следует, что для любой точки M поверхности F существует элементарная поверхность Ф, такая, что 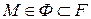, т.е. у каждой точки поверхности существует окрестность, являющаяся элементарной.

Введем понятие координат на поверхности.

Пусть на некоторой поверхности F задано однопараметрическое семейство линий, т.е. каждая линия этого семейства характеризуется определенным значением некоторого параметра. Назовем это семейство правильным, если через каждую точку поверхности проходит одна и только одна линия из данного семейства. Если на поверхности даны два правильных семей­ства, такие, что каждая из линий первого семейства пересекается без касания с каждой линией второго семейства не более чем в одной точке, то говорят, что на поверхности задана координат­ная сеть. Пусть линии первого из семейств, образующих коорди­натную сеть, определяются значениями некоторого параметра и. 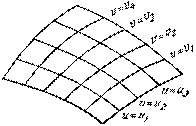А линии второго семейства – значениями некоторого параметра v. Так как по условию через каждую точку поверхности проходит единственная кривая из первого семейства и единственная кривая второго семейства, то положение точки на поверхности однозначно определяется соответствующими этим линиям значениями и₀ и v₀ параметров и и v (рис.6). Параметры и и v, значениями которых определяются линии, составляющие координатную сеть, называются координатами на данной поверхности.

Если на поверх­ности введены каким-либо образом координаты u, v,то говорят, что эта поверхность параметризована параметрами u и v. Каждая точка такой поверхности может быть задана значениями параметров u и v. Но эта же точка может быть задана и своими декартовыми координатами. Следовательно, декартовы координаты точек пара­метризованной поверхности представляют собой функции координат на поверхности.

Пусть u, v – декартовы координаты произвольной точки, принадлежащей , а x, y, z – координаты соответствующей точки поверхности. Тогда координаты x, y, z есть функции координат u, v при отображении f, т.е.

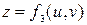, , . (3.1) Эту систему равенств, задающих отображение f области G в пространство, называют уравнениями поверхности в параметрической форме. Здесь u, v называются криволинейными координатами на поверхности. Параметрические уравнения (3.1) при фиксированных значениях u, v задают кривую, лежащую на поверхности. Будем также пользоваться векторной записью уравнения поверхности или .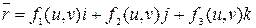

Последняя запись есть векторная функция двух скалярных аргументов u, v.

Замечание 3.1. Уравнение можно рассматривать как частный случай параметрического уравнения, если принять x и y за параметры и положить .

В дальнейшем мы будем рассматривать поверхности, заданные именно параметрическими уравнениями, причем функцию 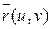будем предполагать непрерывной и имеющей непрерывные частные производ­ные по 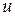и 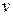. В некоторых случаях, нам придется потребовать также сущест­вования и непрерывности ее частных производных второго порядка.

Не нашли, что искали? Воспользуйтесь поиском: