Выбор независимых переменных 1 страница

В задачах проектирования САУ встречаются параметры двух типов:

1) дискретные (определяемые таблицами ГОСТ, конструкторскими, технологическими нормами и т.п.);

2) непрерывные

Дискретные переменные принимают, обычно, сравнительно небольшое число значений. По ним можно произвести полный или направленный перебор и, таким образом, исключить их из рассмотрения процесса оптимизации по другим, непрерывным независимым переменным. Вышесказанное не исключает существование чисто дискретных задач оптимизации (задач целочисленного программирования), для решения которых существуют специальные методы.

При выборе независимых переменных следует обратить внимание на то, чтобы их было сравнительно немного и чтобы изменение каждой из них действительно оказывало существенное влияние на критерий оптимизируемого процесса. Естественно, что такое пожелание предполагает хорошее знание исследователем своего объекта оптимизации.

Попытка выбора оптимальных всех без исключения параметров для сложных САУ приводит к чрезвычайно сложной математической задаче, трудности решения которой могут быть столь велики, что приемлемое для практики решение вряд ли может быть получено.

1.3. Математические модели объектов оптимизации

Для решения на ЭВМ задач оптимального проектирования конкретных САУ необходимо иметь их математические модели [9,10]. Несмотря на всю сложность и многообразие вышеуказанных систем, процесс построения их математической модели и проверки её адекватности содержит следующие этапы:

1) формализация задачи проектирования;

2) анализ и выделение из общей структуры системы подсистем и элементов подсистем;

3) построение математического описания элементов и их взаимодействия между собой и построение на этой основе математического описания подсистем;

4) построение математического описания в целом на основе математического описания подсистем и их взаимодействия между собой в системе;

5) проверка соответствия числа уравнений, описывающих процессы в системе, числу неизвестных функций – переменных системы. В случае положительного ответа – переход к этапу 6., в противном случае – переход к этапу 2.

6) подготовка к решению математической модели на ЭВМ – выбор алгоритма расчёта, соответствующих его параметров, интервала времени счёта и т.д.

7) анализ результатов расчётов математической модели на ЭВМ с точки зрения соответствия имеющимся результатам экспериментальной проверки всей системы в целом или отдельных подсистем и элементов. В случае положительного ответа – переход к этапу 8, в противном случае - переход к этапу 2.

8) оформление отчёта о работе по составлению математической модели исследуемой системы с указанием всех её переменных, параметров, результатов расчётов и экспериментальной проверки адекватности математического описания.

Переход к этапу 2 обязательно предполагает коррекцию исходного математического описания с целью выполнения условий проверки адекватности математической модели.

Для построения математических моделей объектов оптимизации наиболее часто используются следующие математические зависимости:

1) линейные и нелинейные алгебраические уравнения;

2) трансцендентные уравнения;

3) обыкновенные линейные и нелинейные дифференциальные уравнения и т.д.

Выбор функциональных зависимостей для построения математической модели объекта оптимизации во многом определяется принадлежностью объекта к тому или иному классу (статическим или динамическим объектам), постановкой задачи (детерминированная или стохастическая задача). Этот выбор зависит также и от ряда других факторов, к которым можно отнести следующие: способ задания критерия оптимизации, способ задания ограничений на оптимизируемые параметры, личные склонности и уровень подготовки исследователя.

Задачи оптимизации систем управления имеют ряд особенностей, которые необходимо учитывать при разработке и модификации численных методов оптимизации, разработке соответствующих программ. Основные из этих особенностей следующие:

1) высокая сложность моделей проектируемых систем и связанное с этим большое время анализа модели на ЭВМ;

2) многокритериальный характер задач;

3) большое разнообразие конкретных постановок задач оптимизации и связанная с этим сложность формализации задачи и формирования функции качества;

4) неодинаковая степень влияния параметров на функцию качества;

5) большой диапазон изменения параметров элементов САУ.

Обстоятельство, отмеченное в п. 1, может быть проиллюстрировано на следующем примере. Пусть требуется найти оптимальные параметры САУ, которая является динамической системой со следующей передаточной функцией относительно отклонения :

Поскольку величина 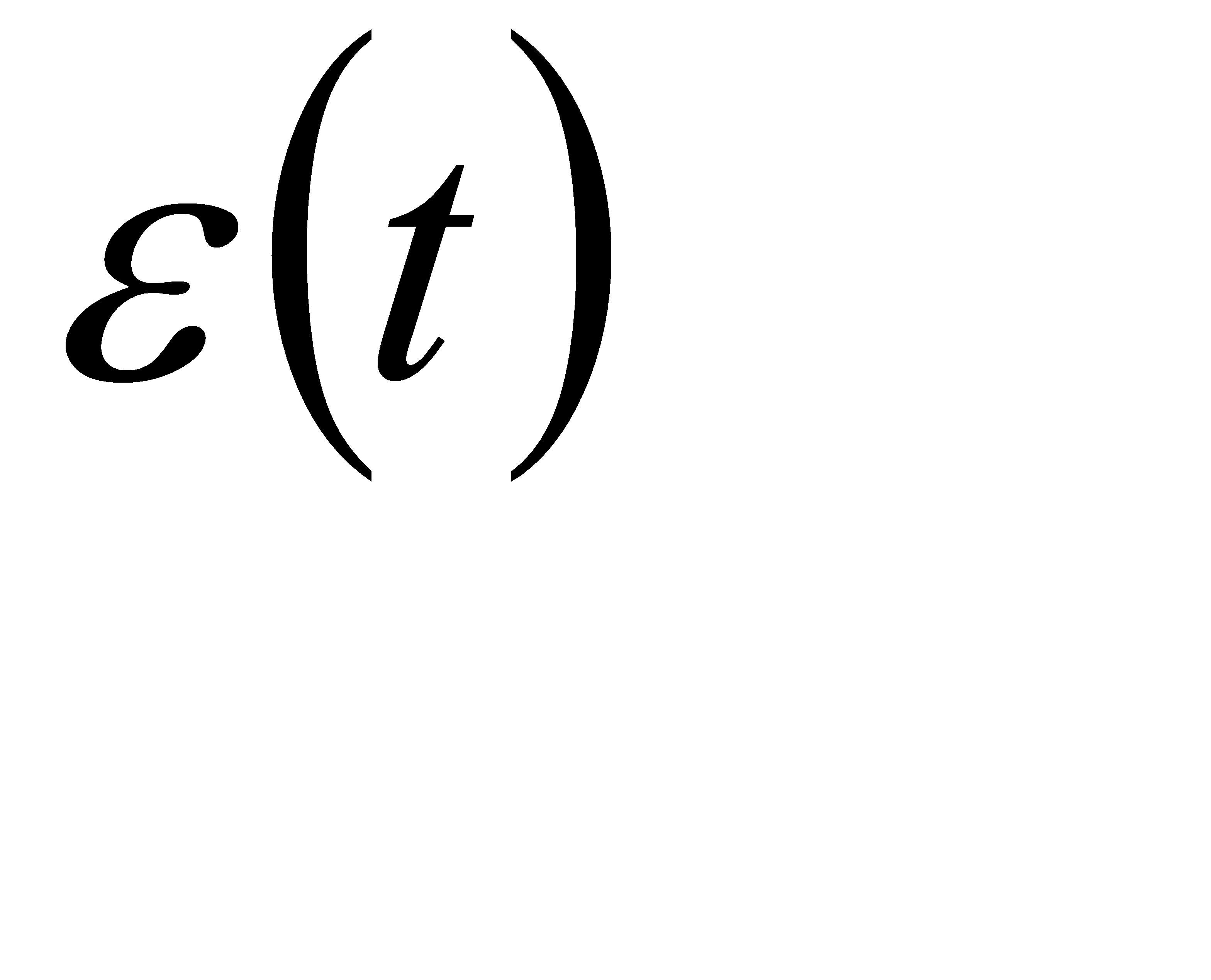зависит от параметров САУ, т.е. от коэффициентов передаточной функции , значит и любой критерий оптимальности Q в который входит 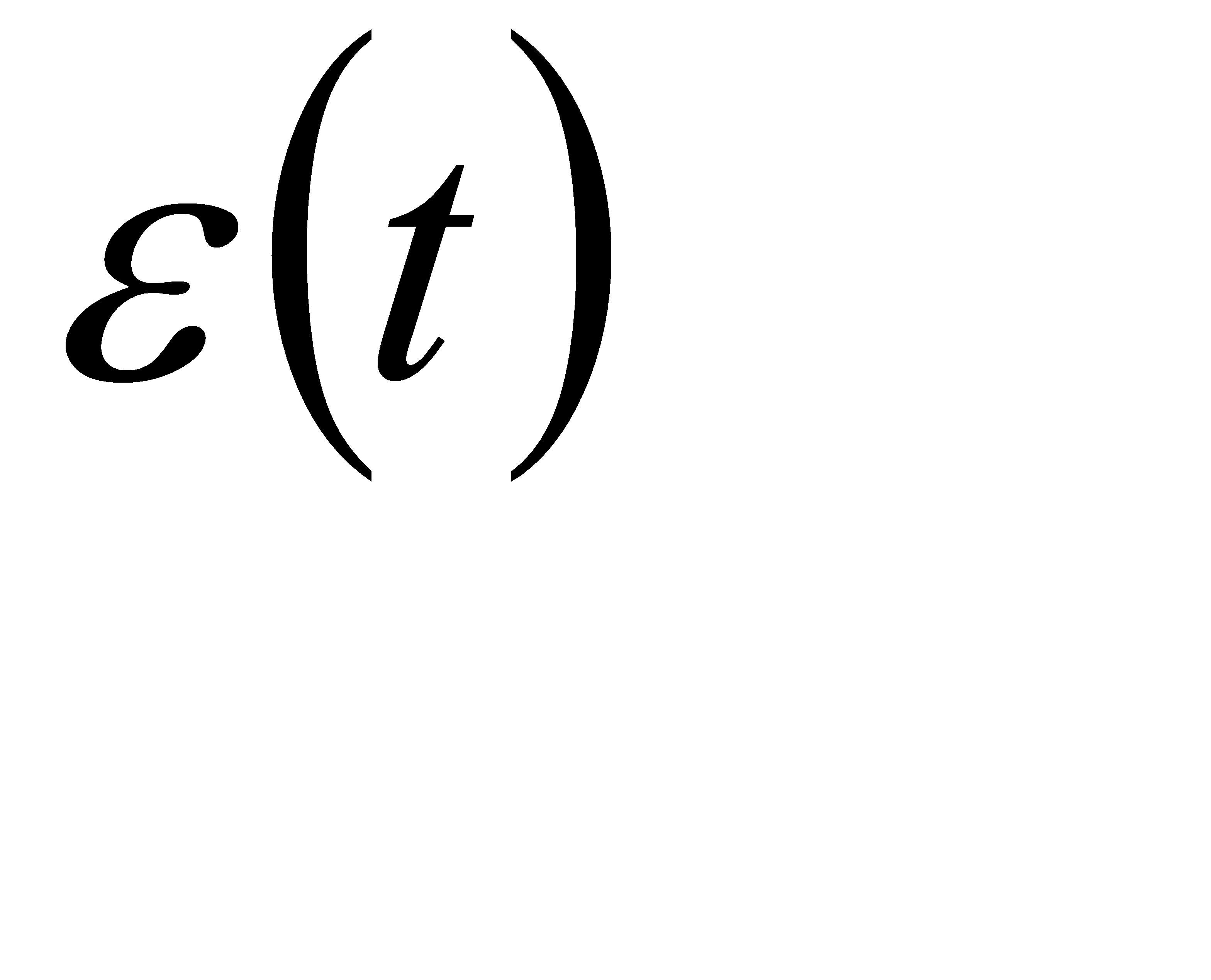(например, ) зависит от параметров САУ. Иными словами,

Однако обычно описать эту зависимость в явном виде либо очень сложно, либо невозможно. Следовательно, приходится искать экстремум неявно заданной функции Q многих переменных.

В дальнейшем будем говорить, что задача НЛП решается с помощью поискового метода оптимизации, если процедура поиска оптимального решения , связана с проведением испытаний (вычислений ) в точках

1.4 Формирование критерия оптимальности

Важнейшим моментом в оптимальном проектировании является выбор и обоснование критерия оптимальности. Выбор критерия оптимальности значительно облегчается, если среди показателей качества системы может быть выделена характеристика, которая, в основном, определяющий качество системы.

Для САУ, например, в зависимости от условий применения такими критериями могут быть перегулированние, время регулирования, интегральная квадратичная оценка и др.

Кроме того, при оптимальном проектировании многих САУ главным является требование обеспечения наилучшей точности работы. Для этого случая однокритериальной оптимизации приведём некоторые из критериев оптимальности.

При синтезе САУ, оптимальных в режиме переходного процесса, за критерий оптимальности можно принять интегральное квадратическое отклонение

где ,

- реакция системы на внешнее воздействие;

– установившееся значение регулируемой величины.

Интегральный показатель качества даёт общую оценку быстроты затухания и значение ошибки 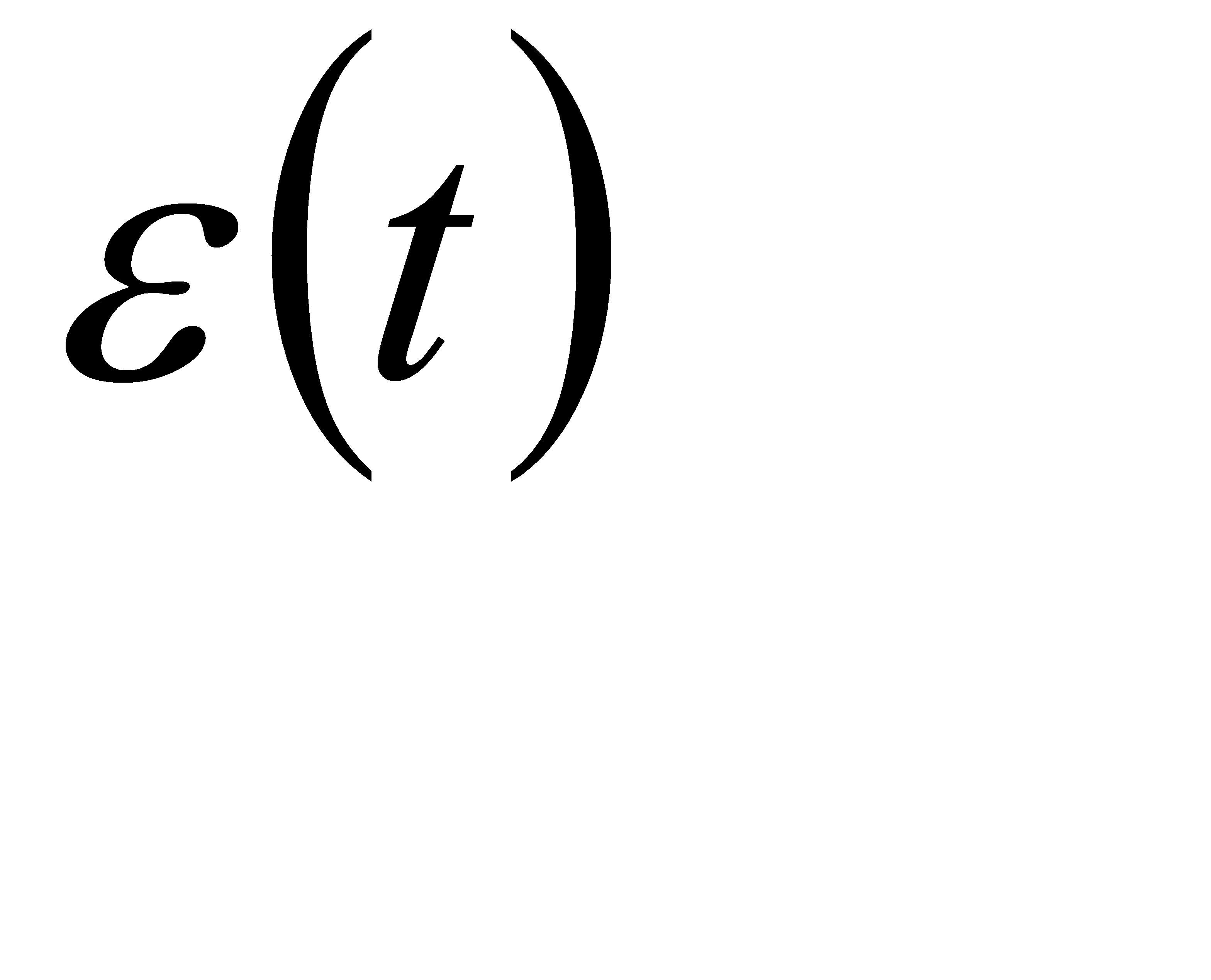САУ в совокупности. Недостаток этого критерия в том, что здесь ничем не ограничивается форма кривой, благодаря чему выбранные параметры приводят к слишком колебательной системе. Поэтому вместо вышеуказанного критерия часто применяют обобщённый критерий

или

где – постоянная величина, характеризующая желаемый переходный процесс.

Однако во многих практических задачах оптимального проектирования часто возникает необходимость получить наилучшие значения для нескольких характеристик объекта, т.е. определить такие независимые переменные 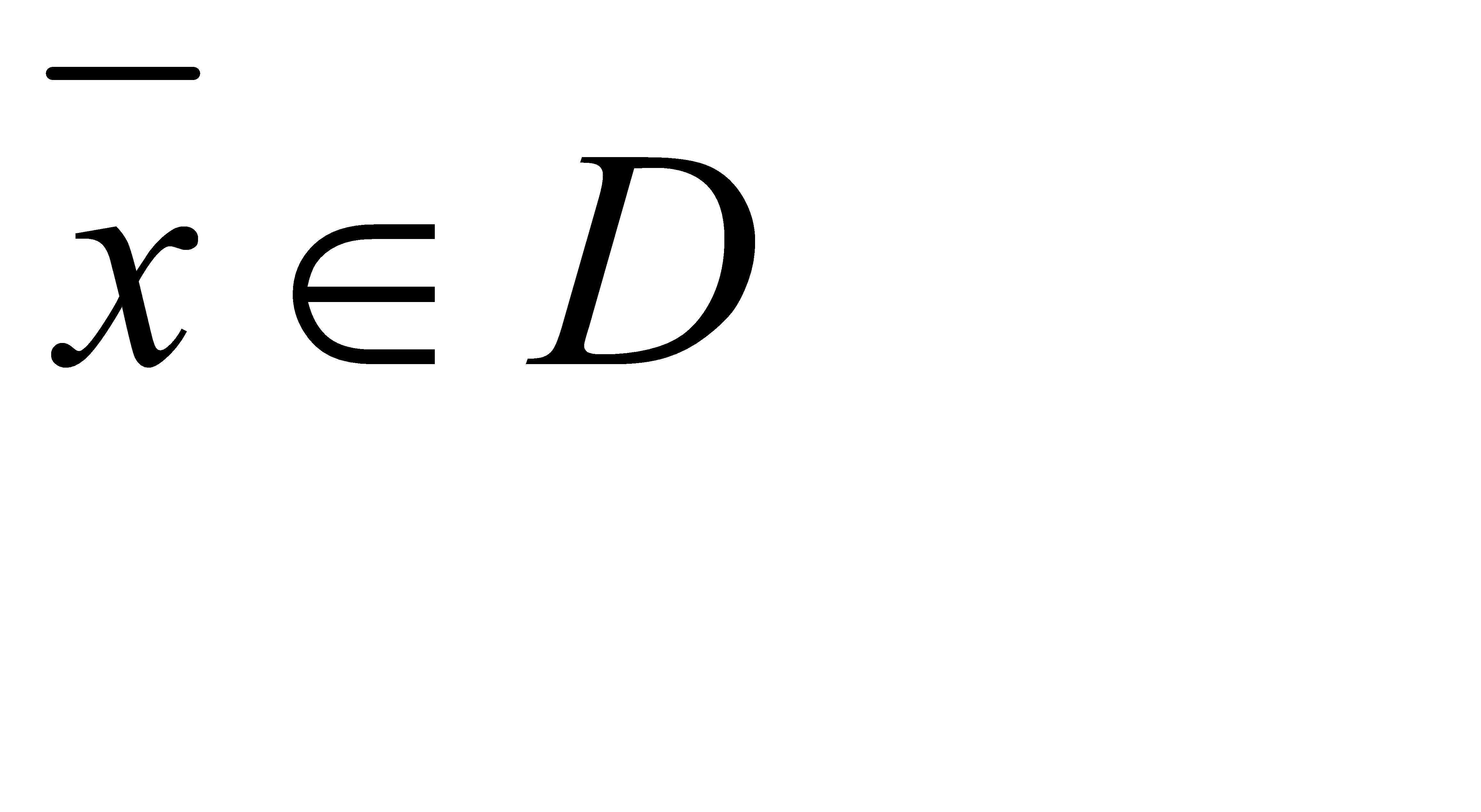, которые обеспечивают экстремум одновременно по всем введенным показателям качества . В связи с этим рассматривают векторный критерий оптимальности

, (1.9)

приводящий к задаче многокритериальной оптимизации (МКО), строгого теоретического обоснования решения которой нет и в настоящее время.

1.5 Векторные критерии оптимальности

В общем случае формирование векторного критерия оптимальности является весьма сложной задачей, требующей от проектировщика всестороннего анализа требований, предъявляемых к объекту проектирования.

Тем не менее, в настоящее время разработан ряд методов решения задачи МКО, среди которых можно выделить два основных направлениях [ 4, 6, 11, 25]:

1) методы, при которых строятся обобщенные критерии;

2) методы последовательной оптимизации.

Одним из наиболее распространенных способов формирования обобщённого критерия является аддитивный учёт частных критериев 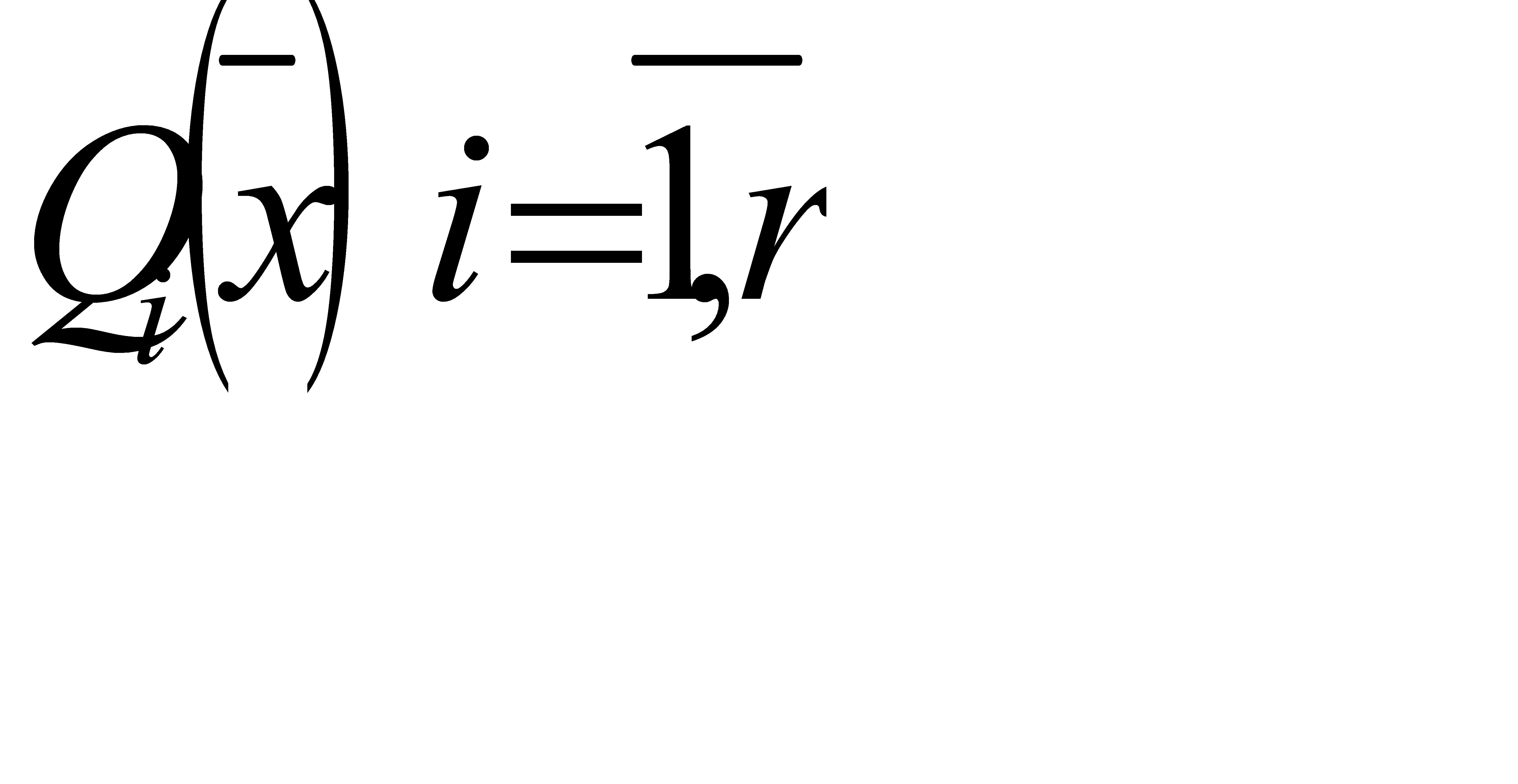, при котором представляется в виде

(1.10)

где – весовые коэффициенты определяемые на основе экспертных оценок или каким-либо другим способом [12].

Примером подобного критерия может служить критерий качества переходных процессов в САУ при решении задачи параметрической оптимизации регуляторов [13].

Суть методов последовательной оптимизации состоит в упорядочении критериев по степени важности и введении допусков 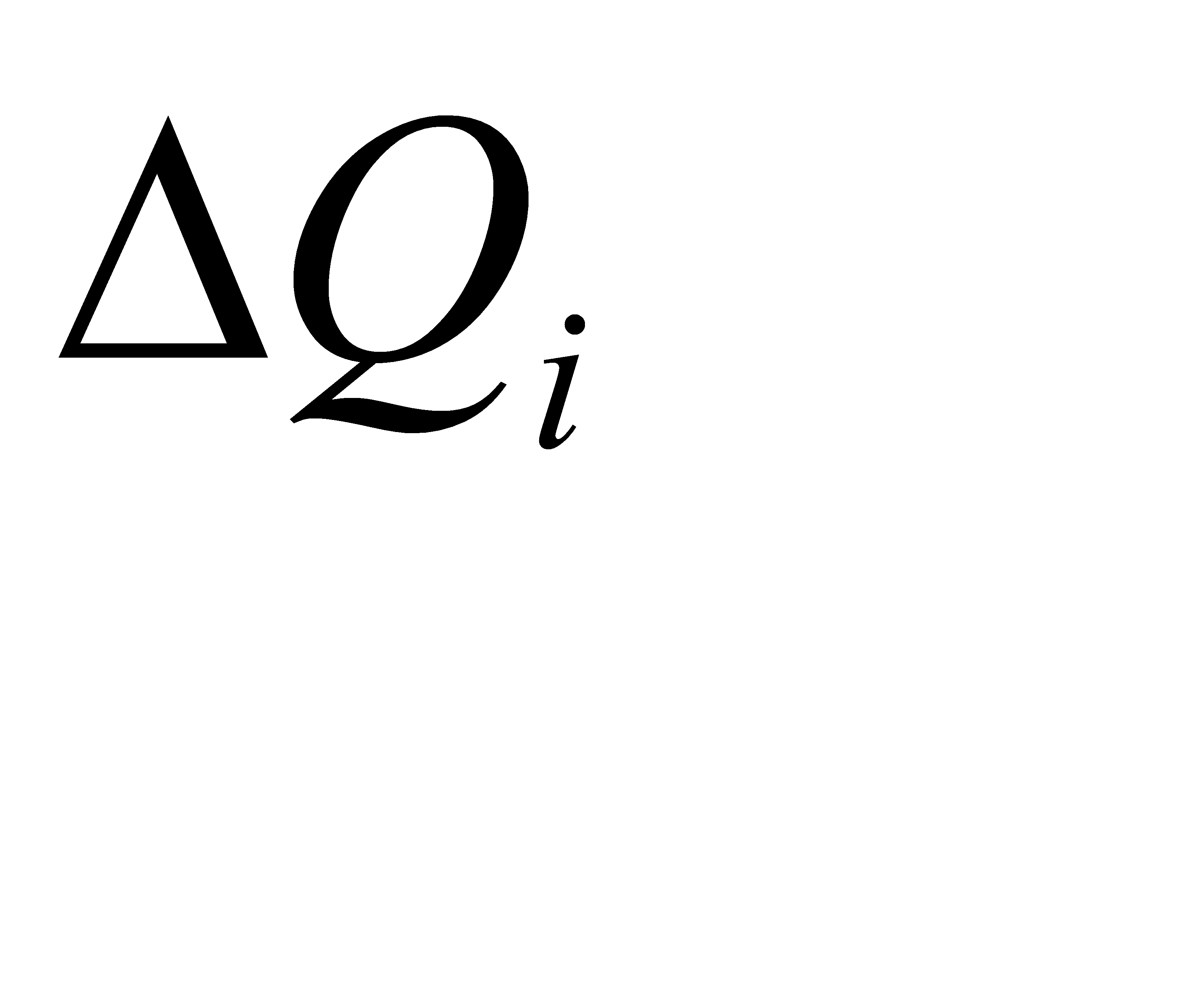по каждому из критериев. Определяется оптимальное решение и соответствующей ему вектор . Для каждого критерия оптимальности задается уступка 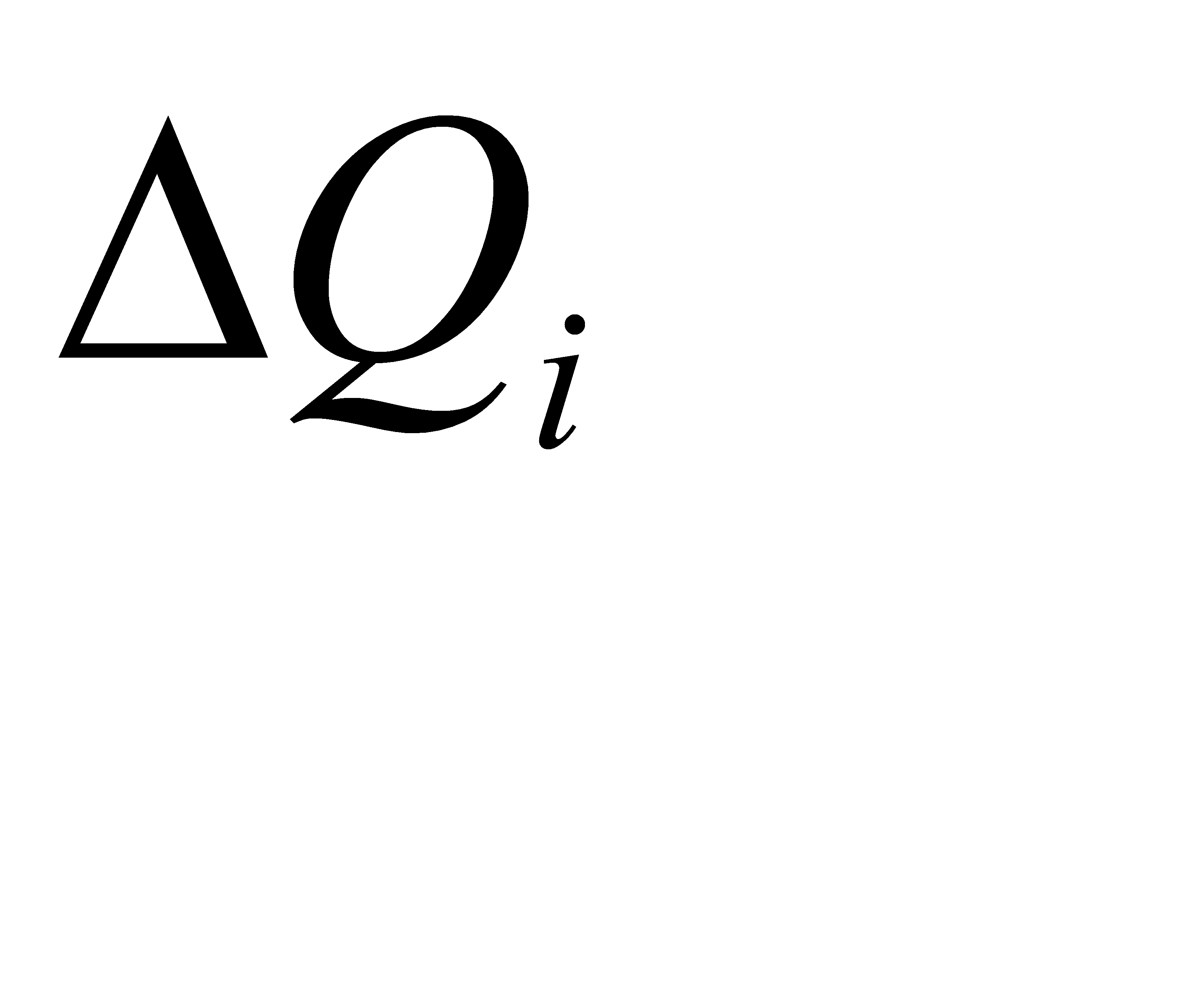и определяется множество решений с удовлетворительными значениями по i – ому критерию оптимальности, такое, что

(1.11)

Использование вектора допусков позволяет произвести поиск варианта, характеристики которого наименее всего отклоняются от соответствующих . Недостаток методов последовательной оптимизации заключается в сложности определения набора уступок, которые существенно влияют на качество проектируемого объекта.

В зависимости от величины 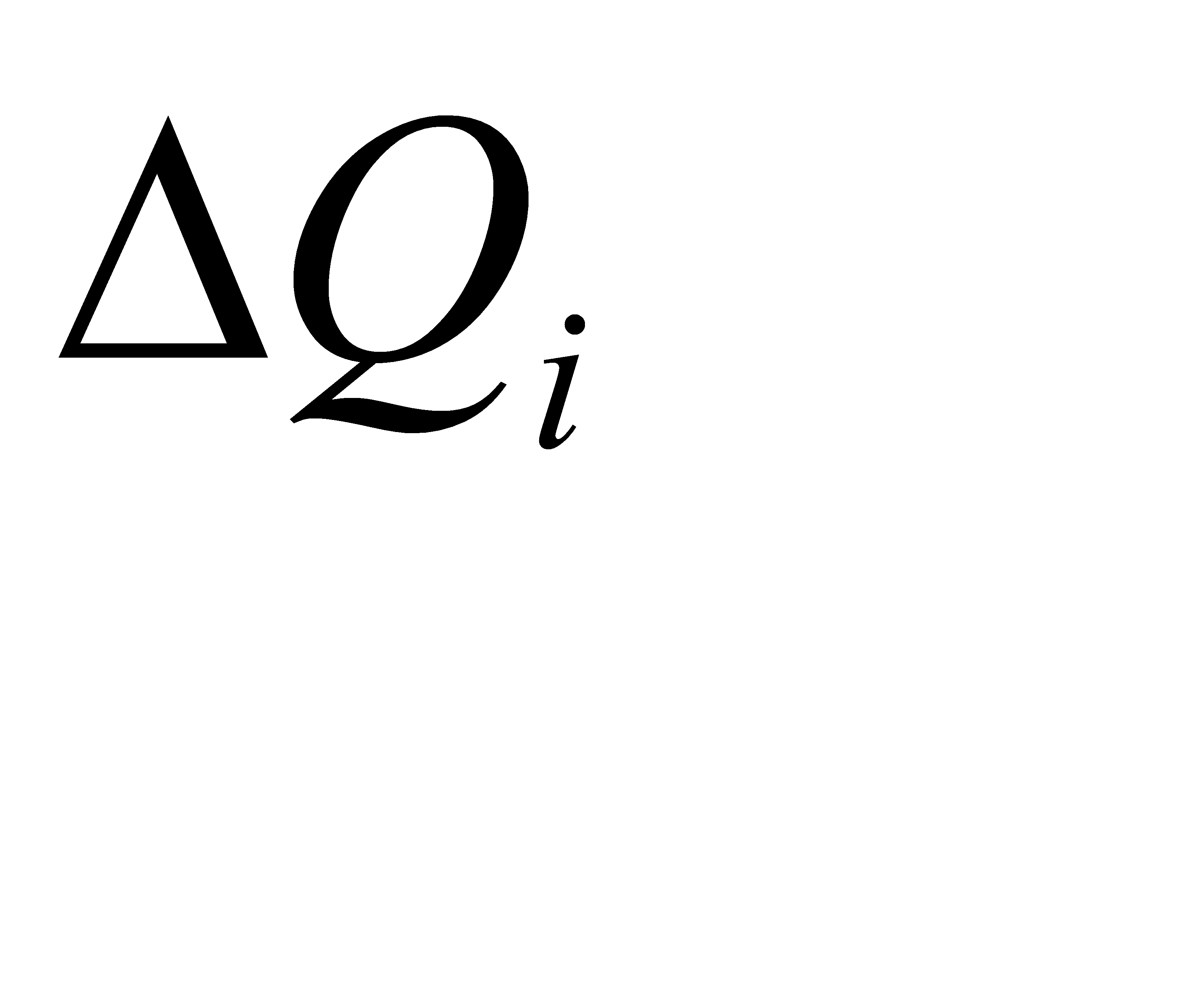можно либо получить неединственное решение, либо вообще не получить решения.

Наряду с вышеуказанными методами значительное распространение получили диалоговые алгоритмы. Промежуточные результаты оптимального проектирования предоставляются проектировщику, который на каждом этапе вырабатывает необходимые для дальнейшего решения задачи управляющие воздействия.

1.6 Ограничения, налагаемые на параметры

и характеристики математической модели

В процессе проектирования численные значения независимых переменных выбираются таким образом, чтобы удовлетворить требованиям, предъявляемым к проектируемым САУ. Эти требования весьма разнообразны и определяются многими факторами, наиболее важными из которых являются следующие:

1) условия физической реализуемости

2) условия эксплуатации, гарантирующие устойчивую и надёжную работу САУ.

3) технологические и конструктивные ограничения на параметры объекта и т.д.

Несмотря на различный физический смысл требований, предъявляемых к объектам проектирования, ограничения могут быть записаны в виде неравенств

где – независимые переменные;

– предельные («-» - минимальные, «+» - максимальные) значения требований, характеризующие область D возможных изменений независимых переменных.

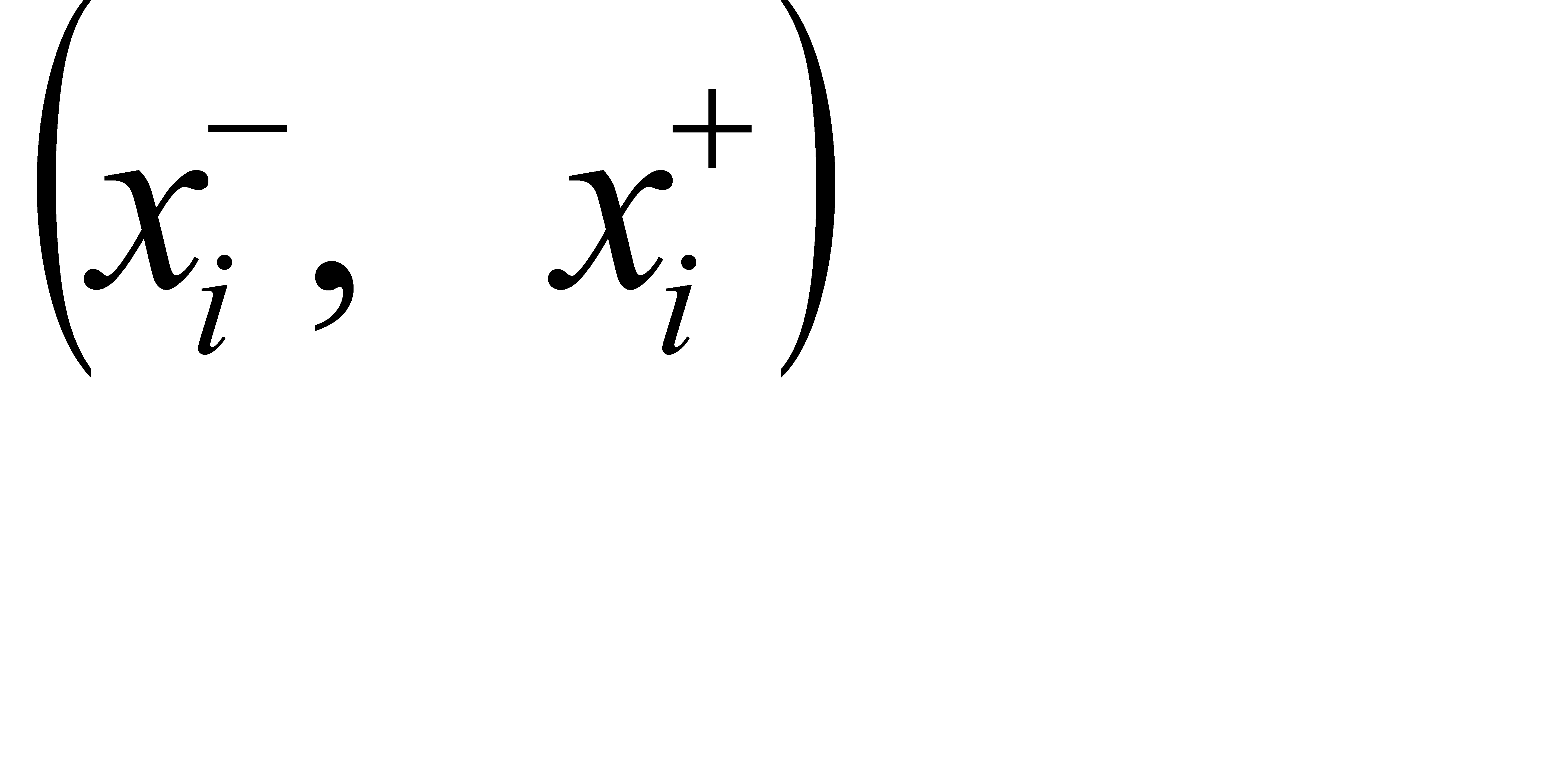Наличие ограничений типа связано с необходимостью избегать физически нереализуемых решений или решений, которые по тем или иным соображениям неприемлемы. Программная реализация учёта таких ограничений достаточно проста. Производится проверка, не находится ли точка близко к границе , а если это так, а вектор направления движения направлен из области поиска, то соответствующая составляющая вектора направления (например, антиградиента) приравнивается нулю. При поиске вдоль выбранного направления производится та же проверка, и в случае её выполнения соответствующий параметр фиксируется на границе области, движение осуществляется по другим параметрам.

Указанные выше ограничения на вектор значительно усложняют задачу оптимизации, для решения которой используют специальные методы, причём задачи с учётом ограничений в виде могут быть сведены к задачам на безусловный экстремум с использованием методов штрафных функций [3, 4, 6, 24].

Основная идея, положенная в основу методов штрафных функций, состоит в замене критерия оптимальности исходной задачи некоторым обобщённым критерием, значения которого совпадают с исходным внутри допустимой области. При выходе из допустимой области или при приближении к ней обобщённый критерий резко возрастает за счёт штрафных функций, зависящих от ограничений. При ограничениях типа примерами штрафных функций могут служить выражения

1) ,

где

- достаточно большая постоянная величина;

2) .

Обобщённым критерием оптимальности согласно методу штрафных функций является выражение

где R >0 – коэффициент штрафа.

при k =1,2, …∞, k – номер этапа поиска.

Поскольку для бесконечно возрастающей последовательности локальные минимумы приближаются к допустимой области, последовательность сходится к локальному оптимуму, расположенному внутри или на границе допустимой области.

2. Методы нелинейного программирования (НЛП)

В данном разделе описываются поисковые методы оптимального проектирования, в котором оптимальное решение определяется с помощью системы рекуррентных соотношений, которые для заданного начального приближения могут быть записаны в следующем виде [4]:

После проведения N шагов поиска, связанных с определением вектора 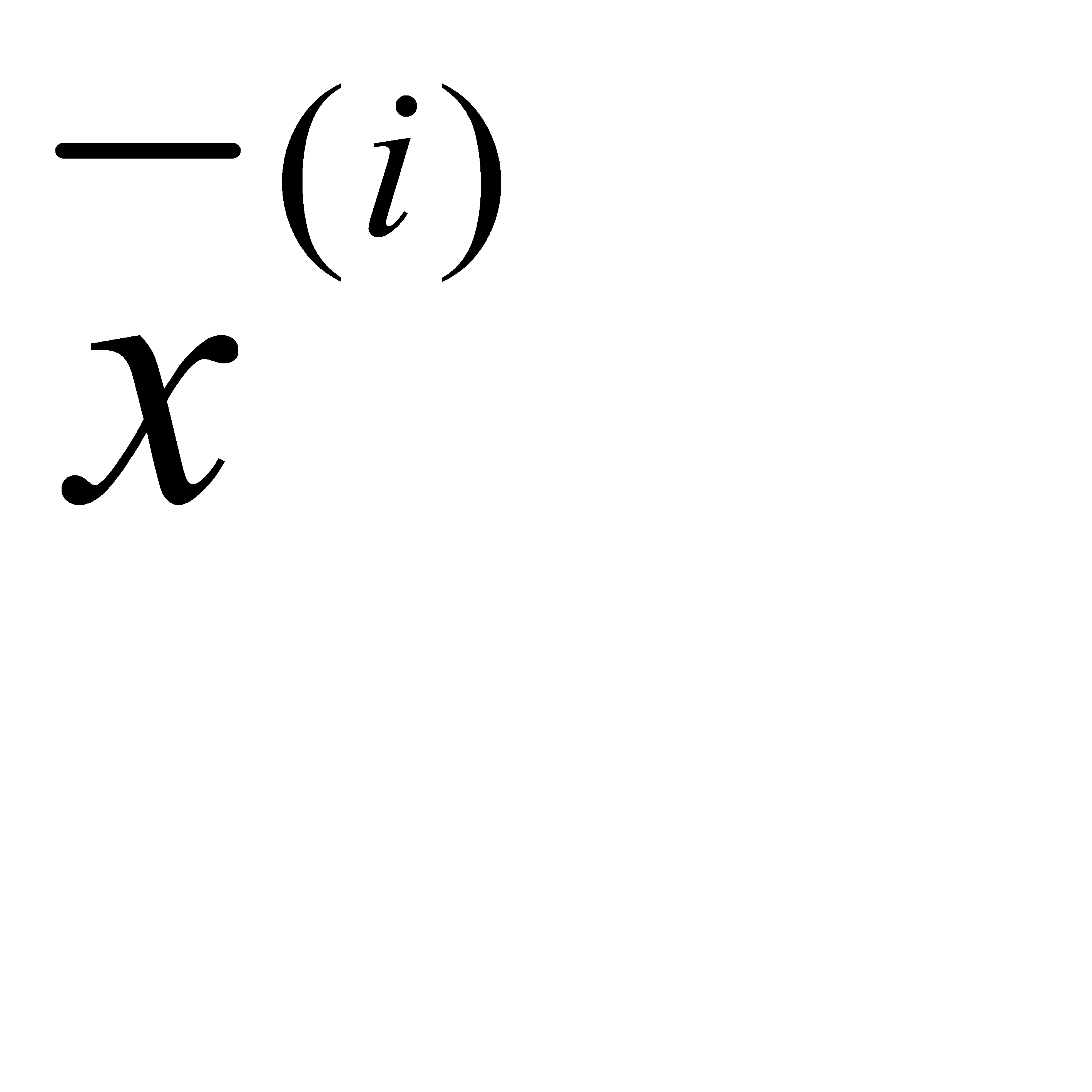, приближённое значение критерия оптимальности выбирается из условия:

Вышеуказанные соотношения являются математической записью методов поисковой оптимизации. Структура вычислений большинства поисковых алгоритмов может быть представлена следующими элементами:

4) определение направления поиска;

5) одномерный поиск, связанный с определением длины шага поиска;

6) управление процессом поиска.

Для решения задач оптимизации функций конечного числа переменных

предложено достаточно много различных алгоритмов и их модификаций (обзоры которых см., например, в [ 1-8 ]). Число алгоритмов и их применений растёт с каждым днём. В связи с этим появилась необходимость в создании определённой классификации поисковых алгоритмов, позволяющей систематизировать работы в этом направлении.

2.1 Классификация методов НЛП

Рассматриваемые в настоящем разделе классификации алгоритмов весьма условны, но, тем не менее, помогают проектировщику ориентироваться в многообразии существующих методов оптимизации. Классификации опираются на известные понятия, связанные с поиском, такие, как непрерывность и дискретность, одно - и многоэкстремальность объекта проектирования и др.

Методы поиска экстремума можно классифицировать по следующим признакам [1-7]. В зависимости от характера экстремума различают методы условной и безусловной, локальной и глобальной оптимизации. Большинство методов оптимизации непосредственно применяется для поиска безусловных локальных экстремумов. Их использование в задачах условной оптимизации возможно, так как существуют методы сведения задач условной оптимизации к безусловной.

В зависимости от количества независимых переменных различают методы одномерного и многомерного поиска. В зависимости от характера информации, используемой для выбора направления поиска различают методы нулевого, первого и второго порядка. В методах первого порядка используются первые производные критерия оптимальности по независимым переменным, составляющие вектор – градиент . Поэтому эти методы называются также градиентными. В методах второго порядка, кроме того, используются вторые производные, составляющие матрицу Гессе. В методах нулевого порядка производные не используются.

По способу получения информации о расположении точки испытания на каждом шаге методы поиска безусловного экстремума можно разделить на детерминированные методы и методы случайного поиска. Детерминированные методы – это методы, в которых функции 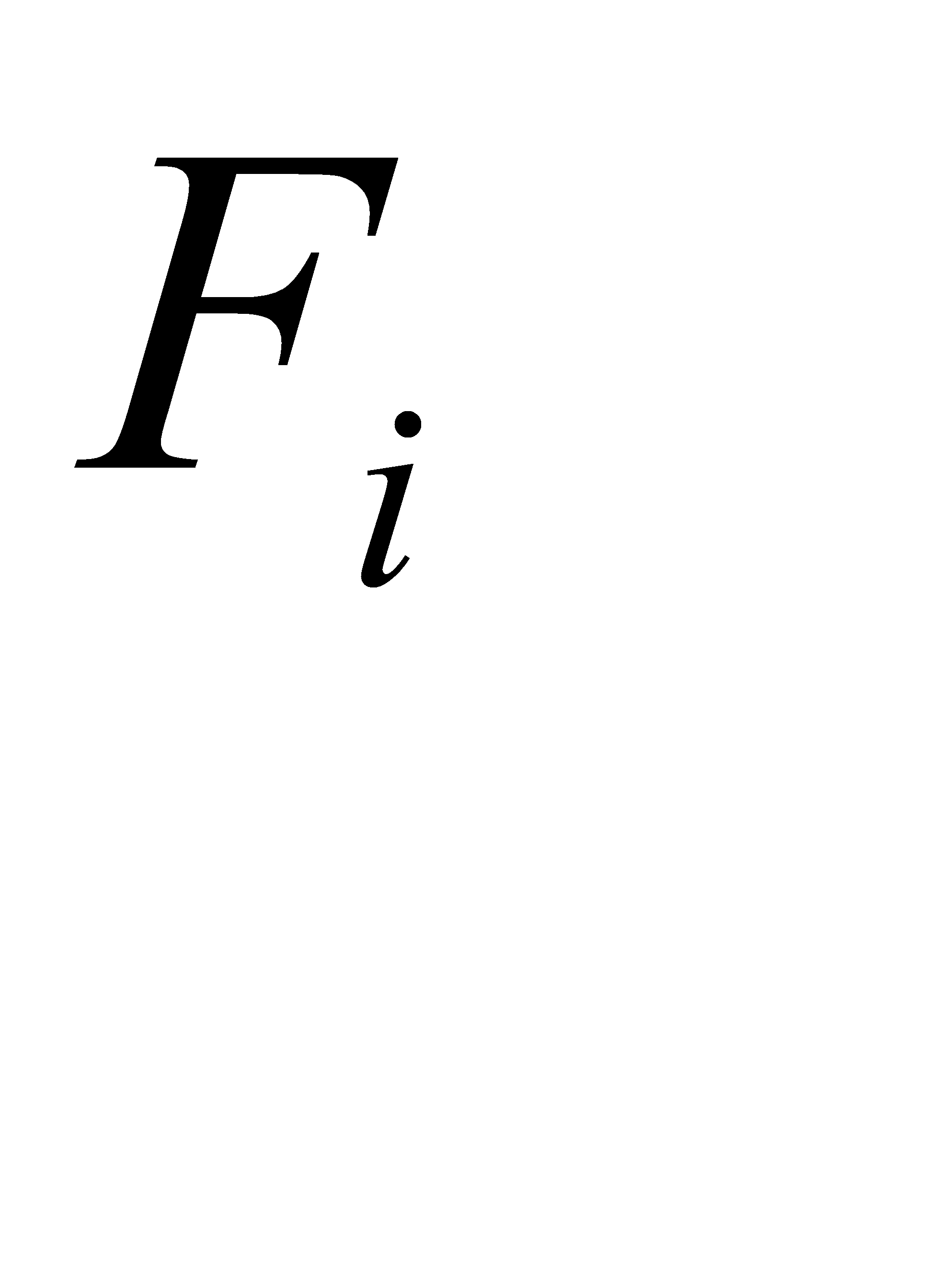являются детерминированными. Методы случайного поиска – это методы, использующие элемент случайности в функции .

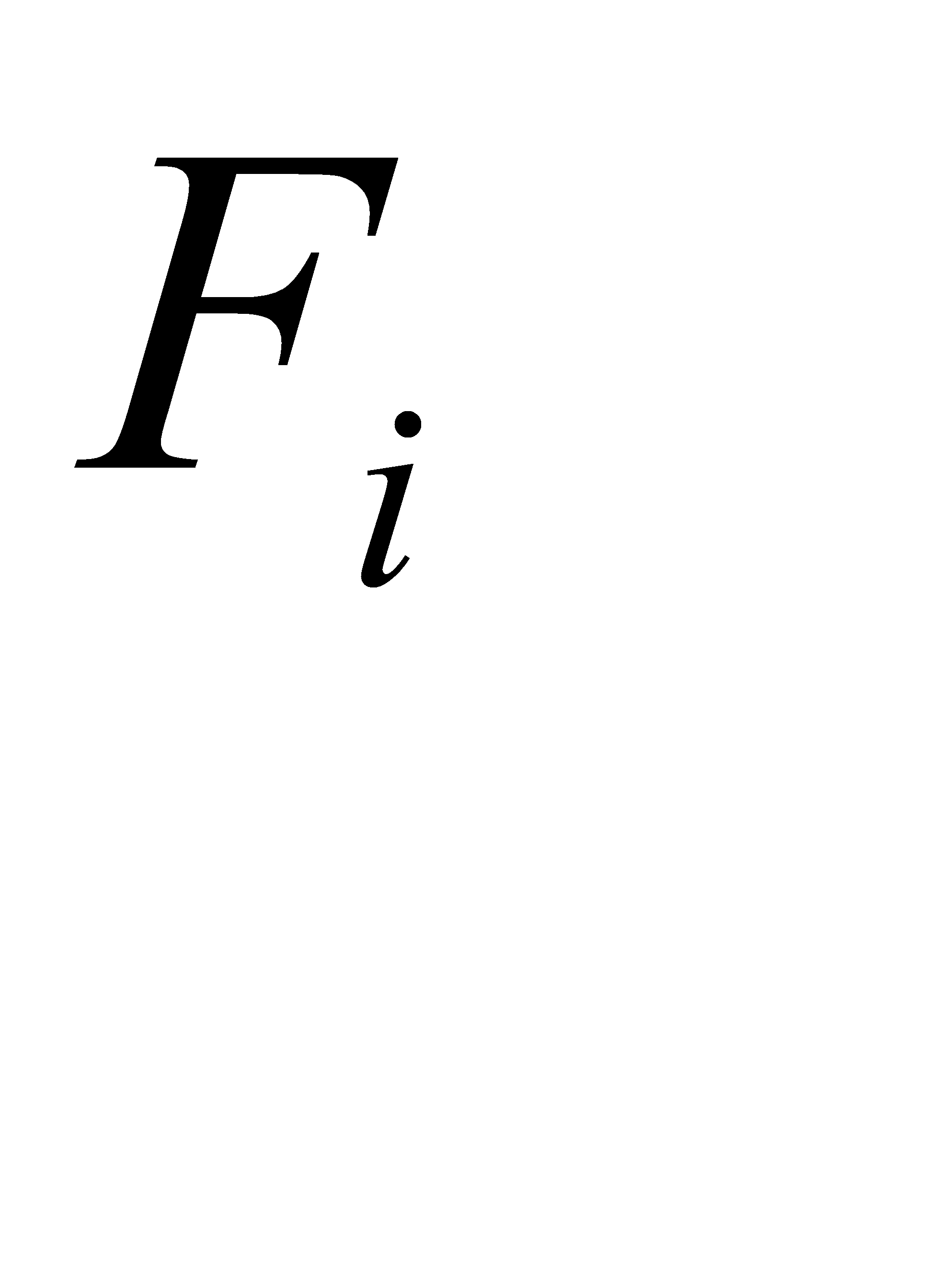Алгоритмом поисковой оптимизации будем называть способ определения начальной точки и конкретной совокупности функций . Следует отметить, что алгоритм может содержать в себе комбинацию различных методов.

В заключение отметим, что возможны и другие принципы классификации методов поисковой оптимизации [4, 6]. Причём даже в рамках этой классификации ниже будут рассмотрены не все методы, а те, которые по мнению автора, являются наиболее предпочтительными при решении задач оптимального проектирования САУ.

Проведённый сравнительный анализ работоспособности и эффективности алгоритмов оптимизации, проведенных, как в нашей стране [14-23 ], так и за рубежом [3, 4, 24 ] позволил выбрать достаточно эффективные просто реализуемые алгоритмы.

Рассматриваемые в работе методы безусловной минимизации принято классифицировать так [4, 5, 7]:

3) методы случайного поиска, в которых используются только значения целевой функции;

4) градиентные методы первого порядка, в которых используются значения целевой функции и её первых производных;

5) квазиньютоновские методы;

6) «овражные» методы поиска;

7) методы поиска глобального экстремума функций многих переменных.

2.2 Методы случайного поиска

Процедуры случайного поиска связаны с алгоритмами, использующими в процессе отыскания минимума функции элемент случайности. Использование последнего позволяет не тратить значительных усилий при поиске на выбор расположения пробных точек, а продвигаться к оптимуму на основе минимальной, достаточно просто получаемой информации.

Методы случайного поиска имеют следующие преимущества:

они пригодны для любой функции , независимо от того, является она унимодальной или нет;

вероятность успеха поиска не зависит от размерности пространства ;

методы достаточно просто учитывают ограничения на область поиска в виде соотношений (1.1) и (1.2).

Программы, реализующие случайные методы поиска значительно проще, чем при использовании детерминированных алгоритмов. Это обстоятельство обусловило широкую популярность методам случайного поиска. Подробное описание таких алгоритмов приведено в работах [25-32], а в [31] дана их обширная библиография, приведён один из вариантов классификации методов случайного поиска.

Случайный поиск с адаптацией шага (Растригин – Тарасенко)

Алгоритм поиска, предложенный авторами [34] записывается в виде рекуррентной формулы

(2.1)

где - изменение независимой на (i+1)-ом шаге поиска, выполненное в соответствии с алгоритмом случайного поиска

, (2.2)

где 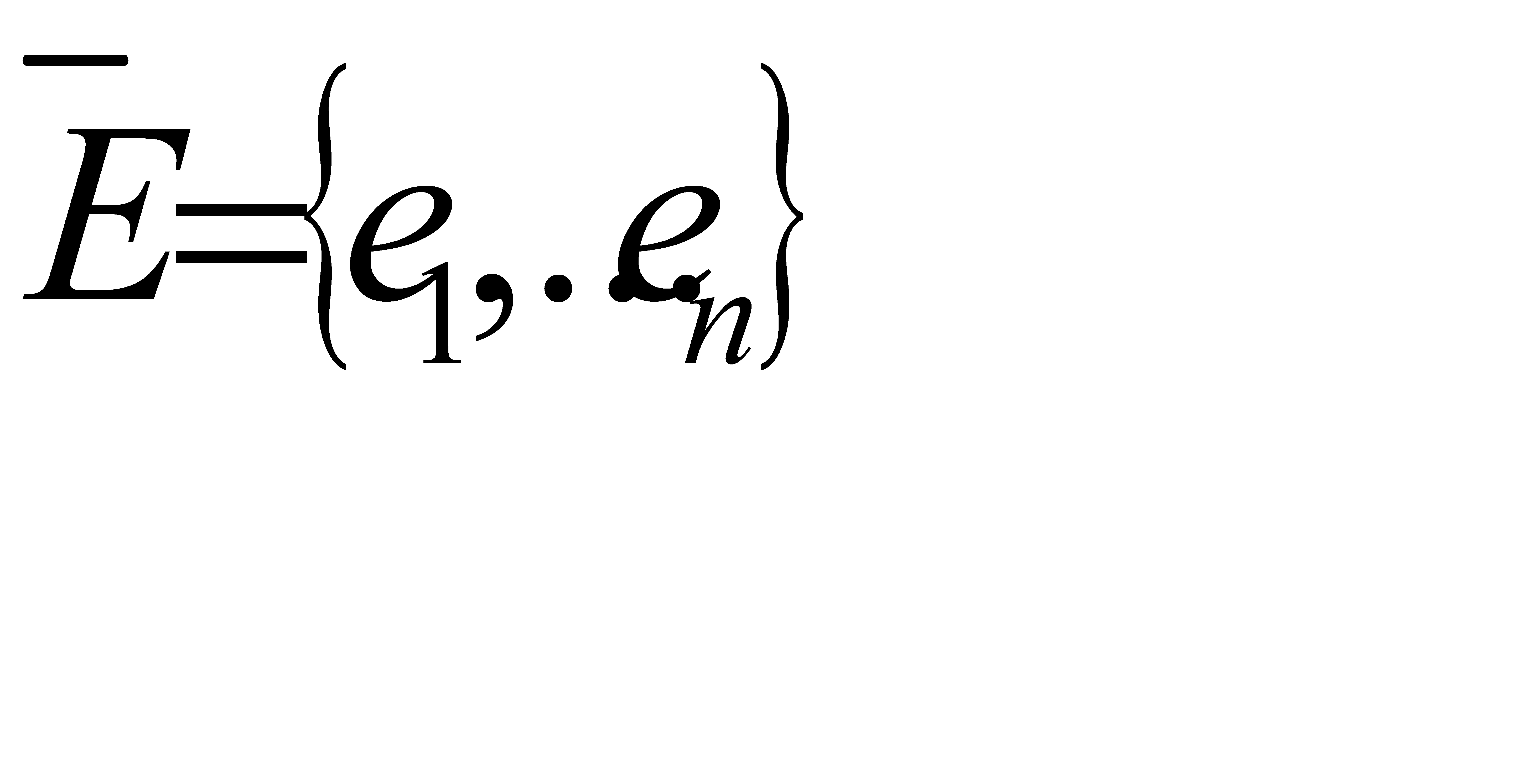- вектор, составляющими которого являются случайные числа, распределенные по равномерному закону в интервале (-1;1).

Управляемым параметром здесь является длина рабочего шага, величина, которого изменяется по некоторому эвристическому алгоритму

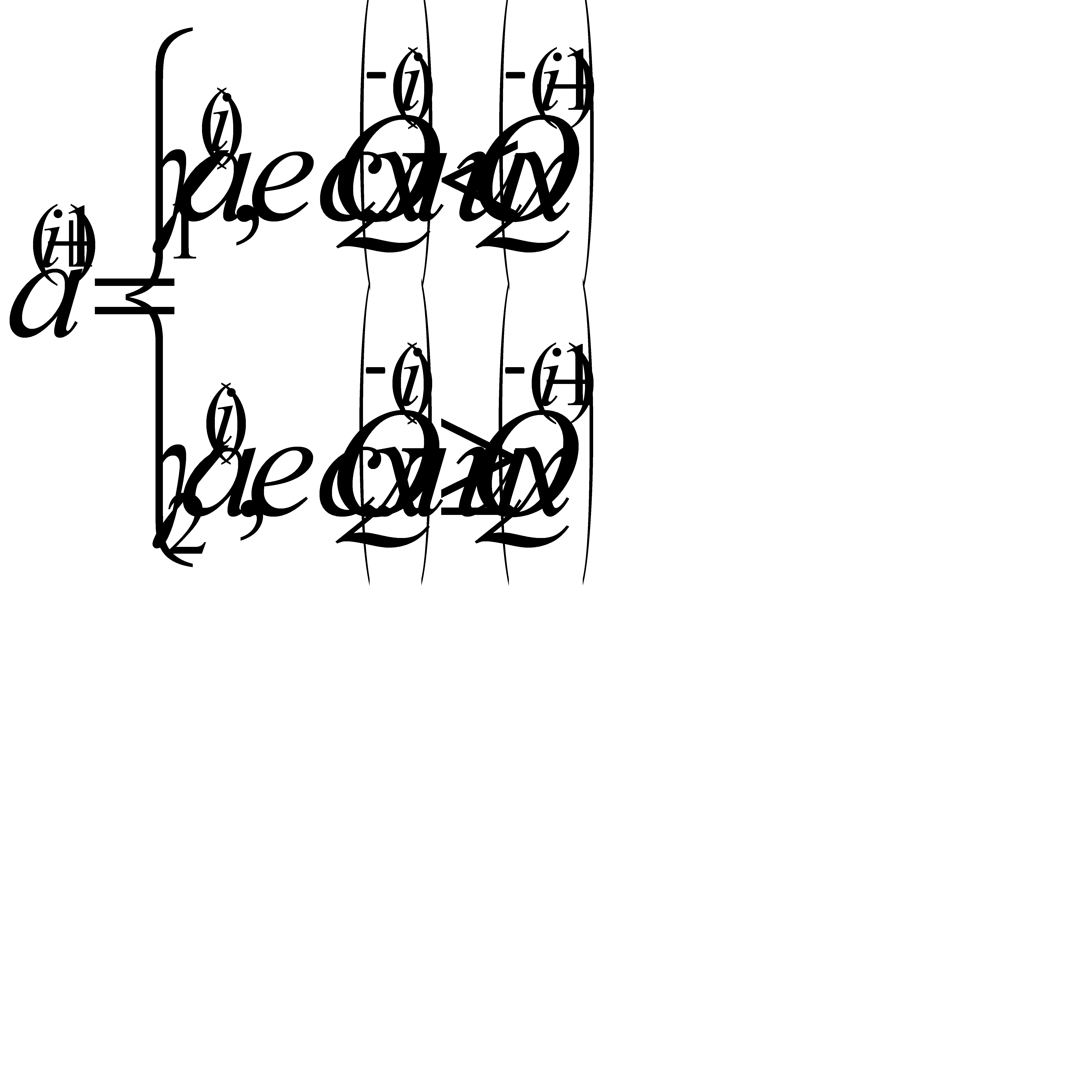(2.3)

где .

Ряд вычислительных экспериментов, проведённых с использованием аппарата планирования эксперимента на тестовый функции

(при n =6) позволил определить диапазон изменения и : , . Вблизи экстремума желательно уменьшить до 0,5. Позднее авторы предложили в своих работах методику определения и причём .

Метод Келли –Уиллинга

В работе [4] предложен алгоритм случайного поиска, суть которого заключается в следующем. После того, как задана начальная точка , строится случайная траектория для последовательности шагов по следующему соотношению

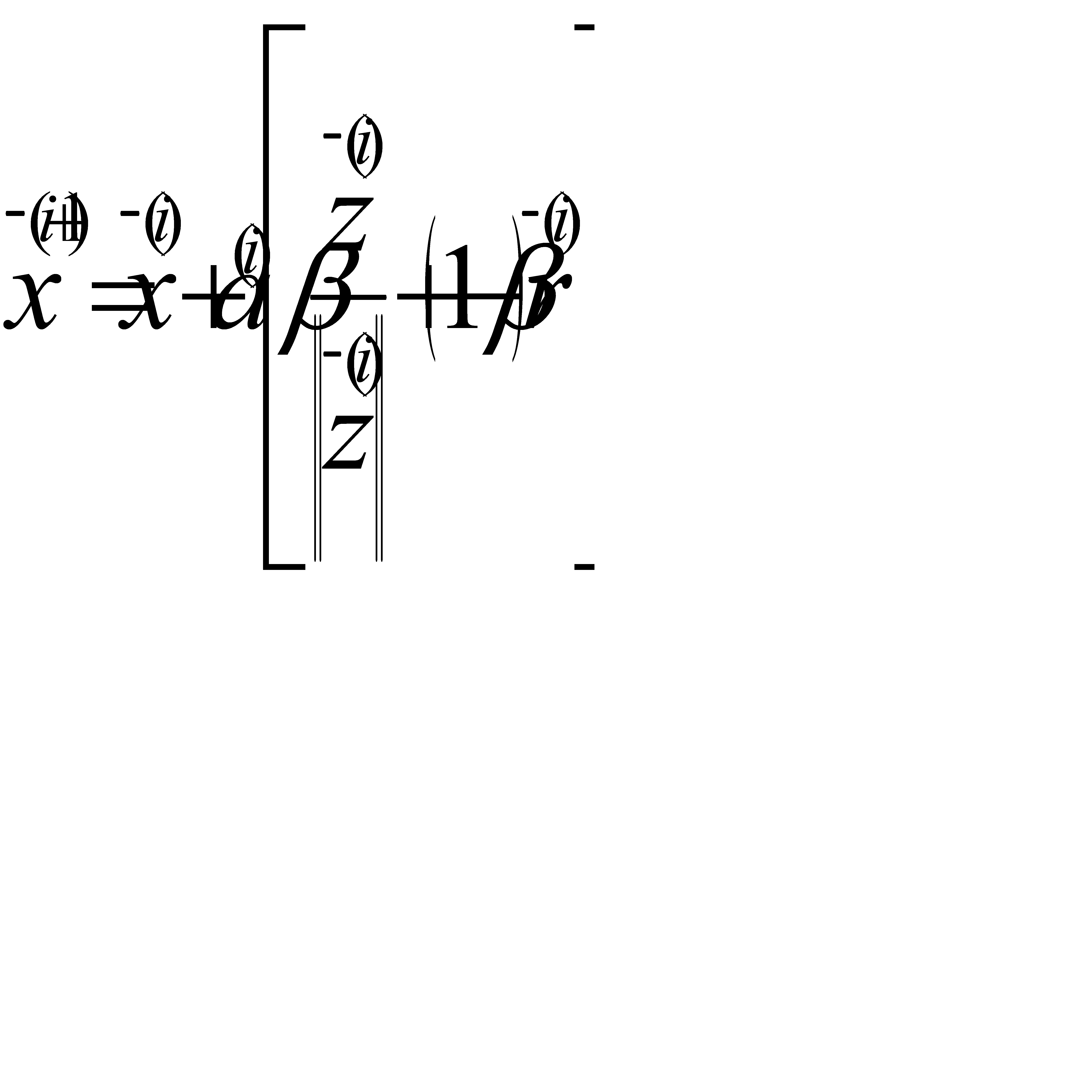(2.4)

где - шаг поиска, который увеличивается после успешного шага и уменьшается после неудачного шага;

- вектор «предыстории», указывающий среднее направление поиска на предыдущих шагах:

(2.5)

- единичный вектор, реализуемый генератором псевдослучайных чисел;

- коэффициент, изменяемый в процессе поиска;

- постоянный весовой множитель;

- вектор масштабных множителей для «подходящего» масштабирования пространства .

На i-ом этапе, чтобы получить , случайный вектор и вектор «предыстории» усредняются. Вектор будет принят (или отвергнут) в зависимости от того выполняется (или нет) неравенство . После того, как принят (или отвергнут), увеличивают (или уменьшают) с помощью некоторого множителя. Поиск прекращается при достижении величины шага минимального значения (0.001).

Значения параметров алгоритма следующие: .

Случайный поиск с самообучением (Растригин – Рипа)

Растригин Л.А. и Рипа К.К. в работе [15] предлагают алгоритм случайного поиска с непрерывным самообучением, способным настраиваться на соседние, более благоприятные направления, что повышает его мобильность по сравнению с покоординатными алгоритмами. Алгоритм записывается в виде рекуррентной формулы:

(2.6)

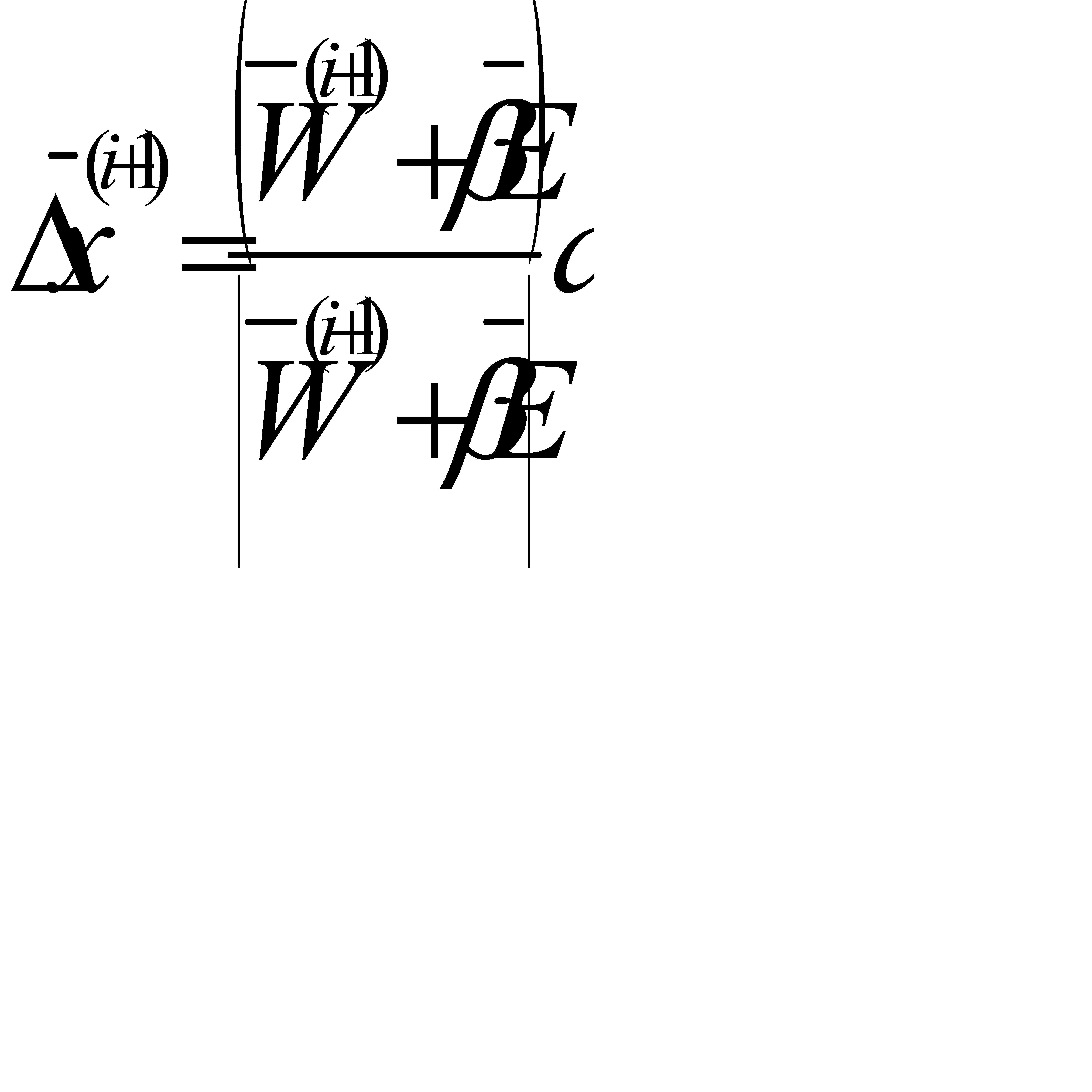(2.7)

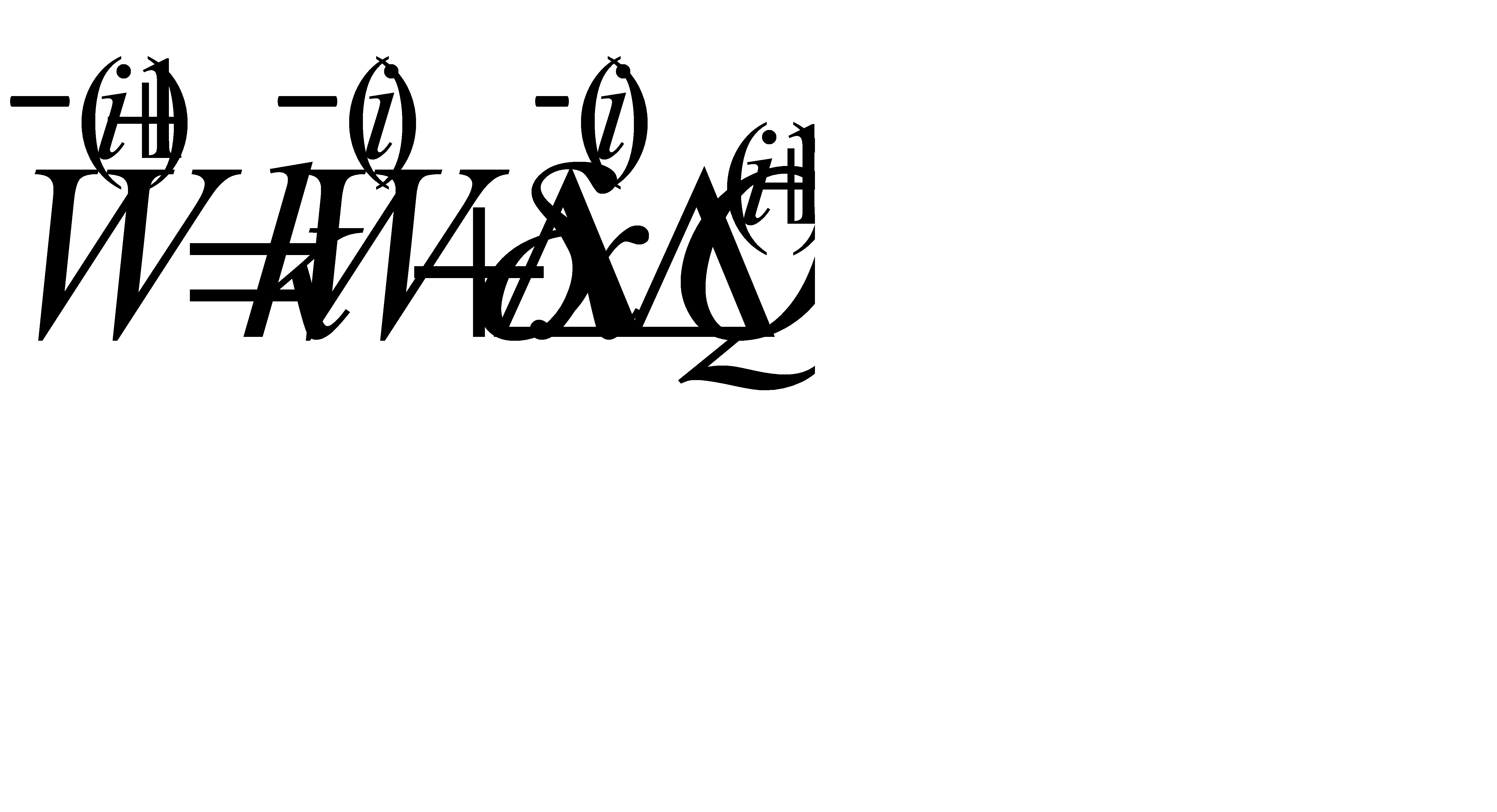, причем ,

где - вектор предпочтительного направления, величина которого ограничивается величиной с;

- смещение независимых переменных на (i+1)-ом шаге поиска;

Не нашли, что искали? Воспользуйтесь поиском: