Теоретичне обґрунтування

Для рішення технологічних завдань експлуатації і по-перше оптимізації швидкості фільтрування та умов промивки сорбційних апаратів важливе значення мають гідравлічні властивості сорбентів.

Гідравлічні властивості сорбентів характеризують падінням тиску в шарі, яке є мірою його гідравлічного опору та розширенням цього шару під впливом потоку рідини. Ці величини залежать від розміру, форми та істинної щільності сорбенту, температури та швидкості рідини. Мета гідравлічних випробувань – вивчення залежності цих величин від швидкості рідини через шар при певних температурах.

При моделюванні промислових сорбційних апаратів виникають складнощі, пов'язані з масштабним ефектом (зниження ефективності апаратів при збільшенні їхніх розмірів, що пов'язане з виникненням гідродинамічних нерівномірностей).

Більшість сорбційних процесів здійснюється в динамічних умовах - умовах спрямованого переміщення фаз розчину через зернистий сорбент (звичайно це частки з невеликим розкидом розмірів від середнього). Застосування зернистих матеріалів викликано особливістю будови їх шару, в якому частки матеріалу чередуються з пустотами або порами шару, які утворюють порові канали, якими рухається вода.

Характерними для опису динаміки є поняття про зерно сорбенту, шар сорбенту і гідравлічні властивості потоку розчину.

Фракційний склад сорбентів, які використовують в практиці очистки води на ТЕС та АЕС, обмежений, з однієї сторони, гідравлічним опором фільтруючого шару (не можна застосовувати надто мілкі матеріали), з іншої – якістю очищеної води (на крупнозернистих матеріалах ефективність очистки нижча).

1. Характеристиками геометрії сорбентів є: форма та щільність зерен, їх кількість в одиниці об'єму, лінійні розміри зерен та їх взаємне розташування.

Пористість зерна сорбенту - частка вільного об'єму в зерні сорбенту і є важливим чинником, що сприяє прискоренню процесу іонного обміну.

Параметри шару зернистого матеріалу: порозність шару, питома поверхня зерен, перепад тиску на шарі, розширення шару сорбенту.

Детальний опис геометрії зернистого шару в зв'язку з складністю звичайно не використовується, і на практиці зернистий шар іоніту розглядається усереднено як однорідне ізотропне середовище, яке характеризується наступними параметрами: порозність, питома поверхня зернистого шару, "живий" переріз (просвіт), "змочений" периметр, гідравлічний радіус, звивистість та інш.

Порозність шару ε - частка вільного об'єму в зернистому шарі - безрозмірна величина; яка дорівнює відношенню об'єму простору між зернами до об'єму апарата, заповненого зернистим матеріалом. Величина ε залежить від форми зерен, стану їх поверхні, характеру упаковки в шарі. Ущільнення можна досягти вібрацією, інтенсивним перемішуванням або утрускою.

Якщо відома питома вага матеріалу, з якого складається гранула ρ₀ і насипна вага шару ρ_нас, то за цими величинами можна розрахувати порозність ε:

(1)

Величина e характеризує взаємне розташування часток у шарі. Для найбільш щільного упакування куль одного розміру, упорядковано розташованих один щодо одного: e_макс.=0,259. При такому упакуванні куля стикається з 12 сусідніми кулями (координаційне число N - число контактів кожної кулі з сусідньою). Найбільш пухка упорядкована система з монодисперсних куль характеризується координаційним числом 6 та має e_мін.=0,476. Комбінацію різних розташувань можна здійснити укладанням монодисперсних куль з будь-яким координаційним числом від 6 до 12 і порозністю 0,259<e<0,476.

Для полідисперсних часток координаційне число може бути значно більше 12, e може наближатись до нуля, але практично 0,3<e<0,5. Для порошкоподібних сорбентів e ~0,4.

Питома поверхня зерен в шарі – сумарна поверхня всіх зерен шару в одиниці об'єму, має розмірність площа/об'єм=1/довжина [м²/м³]. Для шарів приблизно одного діаметру d її можна розрахувати так:

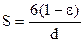, [1/м]. (2)

Таку систему характеризують еквівалентним діаметром d_е, який пов'язаний з величинами порозності та діаметром зерен:

, (3)

а також з порозністю та питомою поверхнею:

, [м]. (4)

Коефіцієнт звивистості. Рідина рухається в порах між частками. Поровий канал звивистий. Коефіцієнт звивистості Т – відношення істинної довжини порового каналу до довжини проекції цього каналу на вісь фільтру, заповненого частками сорбенту. Для шару куль з найбільшою упаковкою Т= 1,41÷1,5.

Коефіцієнт форми – характеризує відхилення форми часток від сферичної, визначає характер обтікання їх потоком рідини. Значення α_ф для сфери дорівнює 1, для куба 0,807, для циліндру з висотою=діаметру – 0,875.

2. Властивості потоку розчину через шар сорбенту визначаються його щільністю, в'язкістю та швидкістю фільтрування. Неоднорідність структури зернистого шару обумовлює і неоднорідність в розподіленні швидкостей рідини.

В якості визначальної можна обрати: 1) середню швидкість потоку w - розраховується на весь переріз фільтру с зернистим шаром; 2) середню швидкість потоку в просторі між зернами u називається швидкістю ковзання (або еквівалентною швидкістю)

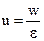(5)

Відношення сил інерції до сил в'язкості оцінюється критерієм Рейнольдса – основним параметром, що визначає структуру потоку та гідравлічний опір зернистого шару:

, (6)

де w – швидкість розчину, м/с; d – характеристичний розмір (діаметр зерна сорбенту), м; ν – коефіцієнт кінематичної в'язкості, м²/с.

Коефіцієнт кінематичної в'язкості дорівнює відношенню коефіцієнту в'язкості рідини до її щільності

, =м²/с (7)

Коефіцієнт в'язкості води = 0,001 кг/(м*с), щільність при 20 ^оС = 1000 кг/м³.

Крім формули (6), що визначає критерій Рейнольдса для зернистих сорбентів в техніці використовують поняття еквівалентного критерію Рейнольдса Re_e, який можна розрахувати:

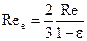, (8)

або

. (9)

Пересування розчину через зернистий шар в кожній точці між зернами повинно підпорядковуватись основним рівнянням гідродинаміки – рівнянням Нав'є-Стокса, які виражають рівність сил інерції сумі всіх діючих сил – перепаду тиску, сили внутрішнього тертя та ваги розчину.

Витрата розчину залежить від гідравлічного опору шару сорбенту. Гідравлічний опір – втрата тиску при проходженні розчину через фільтруючий шар сорбенту.

Для визначення гідравлічного опору на шарі висотою h можна використати формулу Ергуна

, (10)

де f – коефіцієнт опору; ρ – щільність розчину, кг/м³.

Коефіцієнт опору - перепад тиску при обтіканні тіла, який залежить від числа Рейнольдса (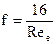 при ламінарному протіканні рідини); для зернистого шару сферичних сорбентів в області Re<2000 можна розрахувати за формулою

, (11)

згідно якої при Re_e≈1 f≈40; Re_e≈10 f≈4; Re_e≈100 f≈0,8 і далі f знижується до 0,45.

Робочий тиск на вході фільтру 0,6 МПа, допустиме зниження на виході – до 0,04 МПа.

Для порівняння використовують розрахунок гідравлічного опору згідно емпіричної формули

, ; (12)

1 мм вод. ст. = 9,81 Па 1 м вод. ст. = 10⁵ Па

Для розрахунку гідравлічного опору зернистого шару сорбентів також рекомендовані формули Козені-Кармана та Блянкмана.

, (13)

де Ко – константа Козені-Кармана (для куль Ко=2); Т – коефіцієнт звивистості; μ – динамічна в'язкість рідини; w – середня швидкість розчину, м/год.

(14)

де ψ – коефіцієнт тертя, який залежить від числа Рейнольдса ψ=24/Re або ; ρ_ж – щільність рідини, w – швидкість руху рідини, м/с; ε – порозність шару; α_ф – коефіцієнт форми.

Для технічних розрахунків гідравлічного опору сипучих іонітів можна застосувати спрощену формулу

, [Па] (15)

Не нашли, что искали? Воспользуйтесь поиском: