Аксиоматическая система механики Ньютона

… Новейшие авторы, отбросив субстанции и скрытые свойства,
стараются подчинить явления природы законам математики.

И. Ньютон

Аксиоматическая система механики Ньютона служит для описания механических явлений в модели «материальная точка». Механические явления связаны с механическим движением тел. Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени, а также изменение его размеров и формы.

Аксиоматическая система обеспечивает

1. Решение конкретных проблем в рамках величин и связей, заданных в аксиоматической системе;

2. Получение новых физических величин и связей в рамках заданной модели;

3. Получение новых аксиоматических систем для более сложных моделей.

В фундаментальную аксиоматическую систему, заданную Ньютоном, входят восемь определений физических величин и три закона. Поскольку подробное описание этих величин содержится в 3 т. «Измерения в физике», то здесь ограничимся рассмотрением законов.

В качестве первого закона движения Ньютон взял закон инерции, известный в частной форме при Галилее. В соответствии с этим законом, материальная точка, не подверженная силам, находится или в покое или движется равномерно и прямолинейно. Такую точку называют свободной, а её движение – свободным движением или движением по инерции. Но любой закон движения имеет смысл только при наличии системы отсчёта. В качестве системы отсчёта Ньютон использовал абсолютное пространство и абсолютное время. Согласно Ньютону, абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остаётся всегда одинаковым и неподвижным. Абсолютное, истинное время само по себе и своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью…

Позднее абсолютное пространство и абсолютное время показали свою несостоятельность, и «ушли» из физики. В современной классической механике постулируют так: «существуют системы отсчёта, в которых все свободные тела движутся прямолинейно и равномерно». Такую систему называют инерциальной системой отсчёта.

Таким образом, суть закона инерции сводится к утверждению, что существует инерциальные системы отсчёта. Это утверждение является обобщением большого числа опытных фактов.

Математическое выражение первого закона .

Второй закон Ньютона постулирует: в инерциальной системе отсчёта приращение импульса материальной точки равна импульсу действующих на точку сил , т.е. , где ‑ результирующая всех сил, равная в соответствии с принципом суперпозиций геометрической сумме сил, действующих на материальную точку.

Импульс силы – физическая величина, равная произведению силы на интервал времени, в течение которого сила действует. Поскольку масса материальной точки постоянна, то закон имеет эквивалентный вид:

или .

т.е. в инерциальной системе отсчёта произведение массы материальной точки на её ускорение равно результирующей силе, действующей на данную материальную точку.

Третий закон гласит: силы, с которыми материальные точки действуют друг на друга, равны по величине и противоположны по направлению. Математическое выражение закона

.

К числу аксиом можно также отнести фундаментальный закон всемирного тяготения: между двумя любыми материальными точками действует сила притяжения, величина которой пропорциональна массам точек и обратно пропорциональна квадрату расстояния между ними. Математическое выражение закона

.

‑ гравитационная постоянная.

Математические эквиваленты законов имеют вид

;

или ;

;

.

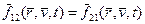Рассмотрим на конкретных примерах возможности аксиоматической системы.

1. Решение локальных проблем при конкретных условиях – это, по сути, решение учебных задач (см. т.2).

2. Объяснение феноменологических законов на базе аксиоматики Ньютона.

3. Получение новых физических величин и новых соотношений в рамках модели «материальная точка».

В качестве примера объяснения феноменологических законов рассмотрим третий закон Кеплера. Кеплер получил этот закон на основе данных, которые много лет собирал его учитель Тихо Браге, проводя астрономические наблюдения за Марсом и другими планетами.

Третий закон гласит: квадраты периодов орбитального движения планет пропорциональны кубам их средних расстояний до Солнца (строго говоря, кубом больших полуосей эллипсов).

Рассмотрим упрощённую модель, считая, что планеты вращаются по круговым орбитам. Считая Солнце неподвижным, возьмём систему отсчёта, связанную с ним. Ввиду больших расстояний между планетами и Солнцем можно взять модель «материальная точка». В этой системе для каждой планеты, вращающейся вокруг Солнца, справедлив второй закон Ньютона

,

где ‑ масса планеты, ‑ её ускорение, ‑ сила притяжения. Поскольку движение вращательное, используем вращательные кинематические величины: ‑ угловую скорость и ‑ период вращения. Если масса Солнца 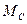, а расстояние между планетой и Солнцем (радиус вращения, то согласно закону движения

.

Учитывая, что , получим

или ,

где ‑ константа, одинаковая для всех планет, вращающихся вокруг Солнца.

Таким образом, феноменологический закон Кеплера является следствием второго закона Ньютона.

Рассмотрим получение новых физических величин и связей при использовании аксиоматики Ньютона в рамках модели «материальная точка». Согласно указаниям Ньютона (см. ранее) надо провести сначала математические исследования в рамках произвольно поставленных условиях, а затем найти условия, при которых полученные соотношения описывают физические явления.

Возьмём второй закон Ньютона и проведём с ним математическую операцию – векторно умножим левую и правую часть на радиус-вектор: . Подставим вместо его выражение через угловое ускорение 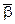и радиус-вектор 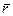, т.е. и заглянем в математический справочник, в котором увидим, что . Введём обозначение и получим соотношение , теперь обозначим и получим выражение . Таким образом, проводя математические операции со вторым законом, получили новое выражение. ‑ скалярная величина, ‑ векторная величина. Согласно определению векторного произведения 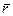и ‑ лежат в одной плоскости, а направлен по прямой, перпендикулярной этой плоскости, и его направление задаёт правило правого винта. Также направлено угловое ускорение 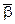. 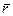По абсолютной величине , где ‑ угол между векторами и .

Теперь надо «обратиться к физике» и посмотреть есть ли физические явления, которые могут быть описаны выведенным соотношением. Опыт показывает, что таким явлением является вращательное движение материальной точки. При этом физические величины, соответствующие выведенным математическим величинам, носят название: ‑ момент инерции точки, 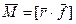‑ момент силы.

Если взять второй закон Ньютона в виде и провести ту же математическую операцию – векторно умножить на 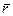, то получим . Здесь новая величина (обозначим ) 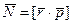и новое соотношение .

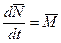Величина 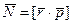получила название момента импульса материальной точки, а соотношение – закон изменения момента импульса материальной точки.

Ещё пример: левую и правую часть второго закона умножим скалярно на скорость:

,

и проведём математические операции:

, ,

, ,

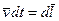где , ‑ угол между векторами и . Обозначим , а , получим новое соотношение .

Опыт показывает, что полученное соотношение может быть использовано при описании физических явлений, при этом физические величины, соответствующие математическим выражениям, носят названия: ‑ кинетическая энергия материальной точки, ‑ работа силы.

Итак, математические операции с математическим эквивалентом второго закона Ньютона приводят к новым физическим величинам и новым связям (физическим законам). Однако ещё раз подчеркнём, что полученные в результате математических операций новые математические формулы, только тогда можно преобразовать в физические законы, когда они подтверждаются опытом.

Итак, мы рассмотрели примеры получения новых физических величин и законов посредством математических операций в рамках модели «материальная точка».

Теперь рассмотрим более сложные модели и получение их законов движения и физических величин на базе аксиоматики Ньютона.

1. Математический маятник – модель, определяемая как материальная точка, подвешенная на невесомом стержне. При отклонении от вертикали маятник совершает движение, которое при небольших углах отклонения от вертикали () описывается функцией синусоидальной или косинусоидальной. Колебания математического маятника полностью описываются аксиоматикой Ньютона (см. т. 2).

2. Система материальных точек – целостный объект, состоящий из взаимодействующих между собой материальных точек. Относительно инерциальной системы отсчёта механическое поведение каждой материальной точки, входящей в систему, описывается законами Ньютона. Однако как целостный объект должен иметь системные свойства, т.е. свойства объекта как целого. При этом свойства объекта как целого надо постулировать и проверить на опыте.

Формализованные в языке математики свойства объекта как целого совместно с уравнениями Ньютона для каждой материальной точки системы позволяют найти уравнение движения целого объекта.

Пример. Рассмотрим совокупность трёх взаимодействующих материальных точек (рис. 5). Для каждой материальной точки справедливы законы Ньютона

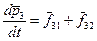
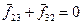
Объединим точки и в систему. Постулируем, что импульс системы материальных точек равен векторной сумме импульсов материальных точек, входящих в систему: . Проведём математические операции: . В нашем случае

.

Соответствующий физический закон имеет вид

.

В инерциальной системе отсчёта приращение импульса системы материальных точек равно импульсу приложенных к системе внешних сил. Внешние силы – силы, приложенные к системе со стороны материальных точек, не входящих в систему. Силы, действующие на материальные точки системы со стороны других материальных точек системы, называют внутренними. В данном примере силы являются внешними, силы ‑ внутренними.

По той же схеме находят закон изменения момента импульса системы материальных точек:

.

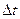Здесь ‑ приращение момента импульса, ‑ момент внешних сил, ‑ интервал времени, в течение которого момент внешних сил действует.

Напомним, что поскольку рассмотренный закон является следствием законов Ньютона, он справедлив в инерциальной системе отсчёта. По той же схеме находят связь между изменением кинетической энергии и работой сил . Закон работает в инерциальной системе отсчёта. Работа является суммой работ и внешних и внутренних сил. При этом внешние и внутренние силы бывают двух видов: консервативные, ‑ работа этих сил не зависит от формы пути, и неконсервативные (диссипативные), ‑ работа этих сил зависит от формы пути. Взаимное расположение материальных точек в системе называют конфигурацией. Конфигурация системы задаётся совокупностью координат материальных точек. Система может находиться в различных конфигурациях. При переводе системы из произвольной конфиг урации в любую другую конфигурацию меняется положение материальных точек системы, а поскольку между точками действуют силы, то производится работа . Работа есть мера передачи энергии, и если она производится за счёт внутренних консервативных сил, то определяется только разностью энергий, обусловленной взаимным расположением точек в конфигурации и . Другими словами, в этом случае . Обычно это соотношение записывают в виде 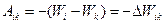. Энергию , обусловленную взаимным расположением материальных точек в системе называют потенциальной. Чтобы найти потенциальную энергию конфигурации , надо условно принять потенциальную энергию конфигурации равной нулю, т.е. .

Система материальных точек имеет много конфигураций. Для нахождения потенциальной энергии выбирают одну конфигурацию, имеющую нулевую энергию, и эта одна конфигурация выбирается произвольно, а значит в количественном отношении потенциальная энергия любой конфигурации определена не однозначно. Однако этот произвол не влияет на физические выводы, поскольку в физике изучаются процессы, а процесс всегда связан с изменением конфигураций и зависит не от абсолютных значений энергии, а от разности энергии различных состояний, т.е. используется формула , а она однозначна. Сумму кинетической и потенциальной энергии системы материальных точек называют полной механической энергией.

Проведём ещё одно математическое исследование. Возьмём геометрическую точку, положение которой задаётся радиусом-вектором , где ‑ массы, а ‑ радиусы вектора материальных точек, входящих в сумму; назовём точку центр-масс. Продифференцируем левую и правую часть

; ,

где ‑ импульс 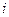-точки.

Получим соотношение: импульс системы материальных точек () равен массе системы (), умноженной на скорость центра масс (): . Продифференцируем правую и левую части: . Поскольку , то 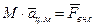, т.е. в инерциальной системе отсчёта произведение массы системы материальных точек на ускорение центра масс равно сумме внешних сил, действующих на систему.

Система материальных точек – общая модель совокупности взаимодействующих между собой материальных точек. При наложении дополнительных условий она переходит в модели меньшей общности. Примерами таких моделей являются:

Абсолютно твёрдое тело – система материальных точек, расстояния между которыми считают неизменными.

Упругое твёрдое тело – твёрдое тело, деформация которого при действии сил на него подчиняется закону Гука: , где ‑ величина силы, ‑ длина недеформированного тела, 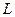‑ длина деформируемого тела, ‑ коэффициент упругости, или жёсткости. Он определяется размерами деформируемого тела и материалом, из которого оно состоит.

Система материальных точек – модель, в которой объект состоит из отдельных частиц, движущихся в пустотных промежутках между ними под действием сил.

В физике существует и другая модель – модель сплошной среды, в которой физические свойства изменяются непрерывно. Для описания модели «сплошная среда» существует два подхода. Первый: использование для описания модели аксиоматики Ньютона. Этот способ использовали Эйлер (динамический подход) и Бернулли (энергетический подход) при разработке ими основ гидродинамики. Эйлер постулировал аксиому, согласно которой второй закон Ньютона справедлив для элемента твёрдого тела или жидкости, выделенного из среды. Используя эту аксиому, Эйлер рассмотрел частицу, имеющую форму параллелепипеда со сторонами 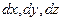, на которую действовали силы со стороны внешней среды, и получил дифференциальное уравнение движения идеальной жидкости. Это уравнение само можно считать аксиомой, из которой были выведены следствия, в частности, известные законы гидростатики Паскаля и Архимеда.

Бернулли использовал энергетический подход – закон сохранения энергии – и получил уравнение, названное его именем. Эффективный подход для этой модели – использование математической теории поля. Математическое поле определяют как область, в каждой точке которой задана скалярная или векторная функция радиуса-вектора. Соответствующие поля называют скалярными или векторными. Математический аппарат теории поля разрабатывался ещё Лапласом и Пуассоном. Математическое понятие «поле» было введено Грином.

Полевая модель чрезвычайно сильно расширяет возможности описания. В теории математического поля есть математические объекты, свойства которых не зависят от системы координат, а зависят только от свойств поля. Это означает, что соответствующие физические величины не зависят от системы отсчёта, а определяются только свойствами поля. Математические объекты, зависящие от свойств поля, называют инвариантами. К ним относятся поток вектора, циркуляция вектора, дивергенция вектора, ротор вектора, градиент (см. Дополнения).

Волновая модель. Видимо, все наблюдали, что если бросить в озеро камень, то по воде начнут быстро разбегаться круги от места попадания камня в воду. При этом мелкие предметы (листики, букашки, щепки и т.п.), лежащие на поверхности воды, начнут вертикальное движение без горизонтального перемещения. Такое возмущение воды носит название волнового, а волны можно определить как изменения состояния среды (возмущения), распространяющиеся в среде без переноса вещества и несущие с собой энергию.

В случае с камнем, упавшим в воду, смещение частиц (вертикальное смещение) происходит в направлении, перпендикулярном направлению распространения волны – такие волны называют поперечными.

Существуют волны, в которых направления распространения волны и смещения частиц среды одинаковы (звук). Такие волны называют продольными.

Волны имеют различные формы: одиночная волна (импульс), ограниченный ряд повторяющихся возмущений (цуг), гармоническая волна.

Гармоническая волна представляет собой бесконечную синусоиду и является фундаментальной волновой моделью. Формула волны:

.

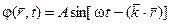
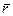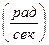‑ величина возмущения в точке с радиусом-вектором в момент времени ; ‑ амплитуда возмущения; ‑ круговая частота ‑ связана с периодом : , где период – время, за которое совершается один полный цикл колебаний. Часто вместо периода используется циклическая частота ; ‑ носит название волнового вектора. По абсолютной величине равен числу волн на отрезке и ориентирован в направлении распространения возмущения; ‑ длина волны ‑ расстояние между двумя соседними максимумами (минимумами) возмущений. Длина волны и период связаны: , где 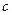‑ скорость распространения возмущения. Выражение, стоящее за в выражении волны, называют фазой: .

,

если волна распространяется вдоль одной оси, например, , то

.

Одной из характеристик волн является вид поверхностей равных фаз, т.е. поверхностей, в любой точке которых в данный момент времени фазы одинаковы. Эти поверхности называют волновыми фронтами.

Соответствующие волны классифицируют по виду поверхностей равных фаз: плоские, сферические, цилиндрические.

Как уже было отмечено, распространение волн связано с переносом энергии в среде от локального возмущения. Количественно он характеризуется вектором плотности потока энергии . Направление совпадает с направлением переноса энергии, а его абсолютная величина равна энергии, переносимой волной за единицу времени через единичную площадь, расположенную перпендикулярно направлению потока. Обычно при расчётах используют связь потока и амплитуда волны : , где зависит от природы волны и свойств среды.

Волны различной природы участвуют в одних и тех же явлениях (интерференции, поляризации, дисперсии), причём наиболее наглядны они в оптике (см. «Оптику»).

Законы сохранения. Существуют физические закономерности, в которых численные значения некоторых физических величин не изменяются со временем в определённых классов процессов. Эти законы называют законами сохранения. Законы сохранения значительно расширяют возможности решения. Используя законы сохранения, решают проблемы даже в тех случаях, когда система очень сложная и динамические законы для неё неизвестны.

Важнейшими законами сохранения, справедливыми для любых изолированных систем, являются законы сохранения энергии, импульса, момента импульса, электрического заряда.

Кроме всеобщих законов сохранения, имеются законы сохранения справедливые локально, т.е. при определённых условиях (например, закон сохранения массы).

Ниже приводятся формулировки законов сохранения в механике.

Закон сохранения полной механической энергии. В инерциальных системах отсчёта полная механическая энергия системы материальных точек сохраняется, если внешние консервативные силы не совершают работы, а внутренние диссипативные силы отсутствуют.

Закон сохранения импульса системы. Если на систему материальных точек в инерциальной системе отсчёта внешние силы не действуют или их сумма равна нулю, то импульс системы сохраняется.

Закон сохранения момента импульса системы. Если в инерциальной системе сумма моментов внешних сил, действующих на систему, равна нулю, то момент импульса системы сохраняется.

Не нашли, что искали? Воспользуйтесь поиском: