Эффективность работы скважины для малых и средних чисел проппанта

Малыми и средними числами проппанта мы считаем всё, что меньше 0.1. Наиболее динамичная деятельность по гидроразрыву (например, фрак-пак) приходится именно на эту категорию, что делает ее чрезвычайно важной с точки зрения проектирования.

Оптимальный дизайн ГРП для средних чисел проппанта можно просто и достаточно кратко представить в аналитической форме. Далее мы покажем, как число проппанта и безразмерный индекс продуктивности связаны с некоторыми другими популярными показателями эффективности работы скважины, такими как функция псевдоскина по Синко-Лею и Саманиего и эквивалентный радиус скважины по Пратсу. По сути дела, дизайны ГРП, основанные на этих связанных показателях работы скважины являются всего лишь предельным случаем средних (низких) чисел проппанта для более всеобъемлющего унифицированного дизайна гидроразрыва.

Пратс [Prats, 1961] ввел концепцию эквивалентного диаметра скважины, являющегося результатом гидроразрыва пласта. Он также показал, что за исключением продольных размеров трещины, все переменные, относящиеся к трещине, воздействуют на работу скважины только через комбинированный параметр — безразмерную проводимость трещины. Когда безразмерная проводимость трещины велика (напр., больше 100), ее поведение аналогично поведению трещины с бесконечной проводимостью. Поведение трещин с бесконечной проводимостью было исследовано позднее Грингартеном и Рейми [Gringarten and Ramey, 1974]. Чтобы охарактеризовать влияние вертикальной трещины с конечной проводимостью на эффективность вертикальной скважины, Синко-Лей и Саманиего [Cinco-Ley and Samaniego, 1981] ввели функцию псевдоскина, которая строго является функцией безразмерной проводимости трещины.

Согласно определению псевдоскин-фактора, безразмерный индекс продуктивности для псевдостационарного режима можно представит как

(3-15)

где — псевдоскин. В обозначениях Пратса этот же индекс продуктивности описывается как

(3-16)

где — эквивалентный радиус скважины. Пратс также использовал относительный эквивалентный радиус скважины, определяемый как .

В формальном представлении Синко-Лея индекс продуктивности описывается как

(3-17)

где — функция псевдоскина относительно полудлины трещины.

В таблице 3-2 показаны связи между этими величинами.

Таблица 3-2. Связи между различными показателями эффективности скважины

Преимущество формального представления Синко-Лея (f -фактор) состоит в том, что для средних (и малых) чисел проппанта величина f зависит только от безразмерной проводимости трещины. Жирная линия на рис. 3-6 показывает f -фактор Синко-Лея как функцию безразмерной проводимости трещины.

Отметьте, что при больших значениях 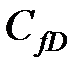выражение для f -фактора стремится к ln(2), что указывает на то, что приток из трещины с бесконечной проводимостью эквивалентен притоку, который в p/2 раз больше, чем приток из той же самой поверхности, свернутой в цилиндр (наподобие стенки огромной скважины). При вычислениях удобно использовать следующее выражение в явном виде:

, где (3-18)

Поскольку относительный радиус скважины по Пратсу также может быть выражен через
f -фактор (см. табл. 3-2), мы получаем эквивалентный результат:

, где (3-19)

Простые аппроксимации кривых, представленные в уравнениях 3-18 и 3-19, действительны только в диапазоне, указанном на рис. 3-6. Для очень больших значений 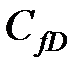можно просто пользоваться предельным значением для уравнения 3-19, равным 0.5, из чего видно, что трещина с бесконечной проводимостью имеет продуктивность, аналогичную воображаемой (громадной) скважине с радиусом .

Достаточно интересно, что поведение трещины по типу трещины с бесконечной проводимостью не означает, что мы выбрали оптимальный способ размещения заданного количества проппанта в пласт.

РИС. 3-6. f -фактор и у -функция по Синко-Лею и Саманиего.

Не нашли, что искали? Воспользуйтесь поиском: